Digitale Werkzeuge in der Schule/Basiswissen Analysis/Von der durchschnittlichen zur lokalen Änderungsrate: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (63 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box|1= Info|2= Dieses Lernpfadkapitel bietet dir einen | {{Box|1= Info|2= Dieses Lernpfadkapitel bietet dir einen Überblick zum Thema Differenzialrechnung: Änderungsraten, Sekanten- und Tangentensteigung sowie deren Anwendungen. | ||
Zuerst erklären wir dir wichtige Begriffe und Zusammenhänge. Danach kannst du selbständig die Aufgaben bearbeiten. | Zuerst erklären wir dir wichtige Begriffe und Zusammenhänge. Danach kannst du selbständig die Aufgaben bearbeiten. | ||
In Aufgaben, die ''<span style="color:#F19E4F>orange</span>'' gefärbt sind, kannst du | Bei den Aufgaben unterscheiden wir folgende Typen: | ||
* In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. | |||
* Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. | |||
* Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''. | |||
* Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. | |||
Viel Erfolg! | |||
|3=Kurzinfo}} | |||
Viel Erfolg | |||
===Grundlegende Begriffe und Formeln=== | ===Grundlegende Begriffe und Formeln=== | ||
| Zeile 16: | Zeile 17: | ||
[[Datei:Niagara bw wasserfall.png|links|rahmenlos|mini]]Der Niagara River verbindet den Eriesee mit dem Ontariosee, in den Horseshoe Falls stürzt er 57m in die Tiefe. Der Graph (schwarz) simuliert den Fall eines Steins von der Kante des Wasserfalls. Die durchschnittliche Fallgeschwindigkeit ist die Veränderung der Höhe in einem Zeitabschnitt. Verschiebe den Regler und beobachte, wie sich die durchschnittliche Geschwindigkeit verändert. Mathematisch gesehen ist die Fallgeschwindigkeit in einem Zeitabschnitt die '''durchschnitlliche Änderungsrate''' der Funktion in einem Intervall. Du ermittelst diese als Steigung der Sekante (rote Linie) zwischen 2 Punkten. | [[Datei:Niagara bw wasserfall.png|links|rahmenlos|mini]]Der Niagara River verbindet den Eriesee mit dem Ontariosee, in den Horseshoe Falls stürzt er 57m in die Tiefe. Der Graph (schwarz) simuliert den Fall eines Steins von der Kante des Wasserfalls. Die durchschnittliche Fallgeschwindigkeit ist die Veränderung der Höhe in einem Zeitabschnitt. Verschiebe den Regler und beobachte, wie sich die durchschnittliche Geschwindigkeit verändert. Mathematisch gesehen ist die Fallgeschwindigkeit in einem Zeitabschnitt die '''durchschnitlliche Änderungsrate''' der Funktion in einem Intervall. Du ermittelst diese als Steigung der Sekante (rote Linie) zwischen 2 Punkten. | ||
Wie schnell ist der Stein beim Aufprall auf die Wasseroberfläche? Verschiebe den Regler ganz nach rechts, aus dem Zeitintervall wird ein Zeitpunkt. Die rote Linie berührt den Graph und in diesem Punkt stimmen die Steigung des Graphen und die Steigung der roten Linie (Tangente) lokal nahezu überein. Die Steigung der Tangente beschreibt das Verhalten der Funktion im Berührungspunkt und wird als '''lokale Änderungsrate ''' bezeichnet. In unserem Fall ist es die momentane Geschwindigkeit beim Aufprall. | Wie schnell ist der Stein beim Aufprall auf die Wasseroberfläche? Verschiebe den Regler ganz nach rechts, aus dem Zeitintervall wird fast ein Zeitpunkt. Die rote Linie berührt den Graph und in diesem Punkt stimmen die Steigung des Graphen und die Steigung der roten Linie (Tangente) lokal nahezu überein. Die Steigung der Tangente beschreibt das Verhalten der Funktion im Berührungspunkt und wird als '''lokale Änderungsrate ''' bezeichnet. In unserem Fall ist es die momentane Geschwindigkeit beim Aufprall. | ||
<ggb_applet id="gr9yngqa" width="100%" height="100%" border="888888" /> | <ggb_applet id="gr9yngqa" width="100%" height="100%" border="888888" /> | ||
| Zeile 33: | Zeile 34: | ||
{{Box|1=Merke| | {{Box|1=Merke| | ||
2= '''Die lokale Änderungsrate''' in einem Punkt nennt man '''Differenzialquotient oder Ableitung in einem Punkt''' | 2= '''Die lokale Änderungsrate''' in einem Punkt nennt man '''Differenzialquotient oder Ableitung in einem Punkt'''. Man berechnet diesen als Grenzwert (du schreibst dafür <math>\lim</math>) der Sekantensteigungen: | ||
<math>f'(x)=\lim_{x_2 \to \ x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1}</math> | <math>f'(x)=\lim_{x_2 \to \ x_1}\frac{f(x_2)-f(x_1)}{x_2-x_1}</math> | ||
| Zeile 46: | Zeile 47: | ||
{{Box|1= <span style="color: orange"></span>Aufgabe 1: Durchschnittliche Änderungsrate | {{Box|1= <span style="color: orange"></span>Aufgabe 1: Durchschnittliche Änderungsrate | ||
|2= Bestimme die durchschnittlichen Änderungsraten der Funktionen in den vorgegebenen Intervallen. Du benötigst für die Aufgabe Papier, Stifte und evtl. einen Taschenrechner. | |2= Bestimme die durchschnittlichen Änderungsraten der Funktionen in den vorgegebenen Intervallen. Du benötigst für die Aufgabe Papier, Stifte und evtl. einen Taschenrechner. | ||
'''a)''' <math>f(x) = \tfrac{1}{2}x^2 - \tfrac{3}{2}</math> in dem Intervall [1; 2] | '''a)''' <math>f(x) = \tfrac{1}{2}x^2 - \tfrac{3}{2}</math> in dem Intervall [1; 2] | ||
{{Lösung versteckt|1 = Für die Berechnung der durchschnittlichen Änderungsrate schau dir die Formel in dem ersten Merkkasten an. Für <math>x_1</math> und <math>x_2</math> setze die Intervallgrenzen ein. Z.B. 2 und 3 für das Intervall [2;3] |2=Tipp|3=Tipp}} | |||
{{Lösung versteckt|1 = Die durchschnittliche Änderung auf dem Intervall beträgt <math>\tfrac{3}{2}</math>. {{Lösung versteckt|1= Setze die Werte wie folgt in die Formel ein: <math>\frac{f(2) - f(1)}{2-1} = \frac{\frac{1}{2}-(-1)}{2-1} = \frac{3}{2}</math>|2= Lösungsweg|3= Lösungsweg}}|2=Lösung|3=Lösung}} | {{Lösung versteckt|1 = Die durchschnittliche Änderung auf dem Intervall beträgt <math>\tfrac{3}{2}</math>. {{Lösung versteckt|1= Setze die Werte wie folgt in die Formel ein: <math>\frac{f(2) - f(1)}{2-1} = \frac{\frac{1}{2}-(-1)}{2-1} = \frac{3}{2}</math>|2= Lösungsweg|3= Lösungsweg}}|2=Lösung|3=Lösung}} | ||
'''b)''' <math>g(x) = x^3 - 0,2x - 3</math> in dem Intervall [-2; -1] | '''b)''' <math>g(x) = x^3 - 0,2x - 3</math> in dem Intervall [-2; -1] | ||
{{Lösung versteckt|1 = Für die Berechnung der durchschnittlichen Änderungsrate schau dir die Formel in dem ersten Merkkasten an. Für <math>x_1</math> und <math>x_2</math> setze die Intervallgrenzen ein. Z.B. 2 und 3 für das Intervall [2;3] |2=Tipp|3=Tipp}} | |||
{{Lösung versteckt|1 = Die durchschnittliche Änderung auf dem Intervall beträgt 6,8. {{Lösung versteckt|1=Wie komme ich zu meiner Lösung? Setze die Werte wie folgt in die Formel ein: <math>\frac{g(-1) - g(-2)}{-1-(-2)} = \frac{-3,8-(-10,6)}{-1-(-2)} = 6,8</math>|2=Lösungsweg|3= Lösungsweg}}|2=Lösung|3=Lösung}} | {{Lösung versteckt|1 = Die durchschnittliche Änderung auf dem Intervall beträgt 6,8. {{Lösung versteckt|1=Wie komme ich zu meiner Lösung? Setze die Werte wie folgt in die Formel ein: <math>\frac{g(-1) - g(-2)}{-1-(-2)} = \frac{-3,8-(-10,6)}{-1-(-2)} = 6,8</math>|2=Lösungsweg|3= Lösungsweg}}|2=Lösung|3=Lösung}} | ||
'''c)''' <math>h(x) = \tfrac{1}{4}x^2</math> in dem Intervall [1,99; 2,01] Überlege, was in dem Intervall mit der Sekante passiert. | '''c)''' <math>h(x) = \tfrac{1}{4}x^2</math> in dem Intervall [1,99; 2,01]. | ||
Überlege, was in dem Intervall mit der Sekante passiert. | |||
{{Lösung versteckt|1 = Für die Berechnung der durchschnittlichen Änderungsrate schau dir die Formel in dem ersten Merkkasten an. Für <math>x_1</math> und <math>x_2</math> setze die Intervallgrenzen ein. Z.B. 2 und 3 für das Intervall [2;3] |2=Tipp|3=Tipp}} | |||
{{Lösung versteckt|1 = Die durchschnittliche Änderung auf dem Intervall beträgt 1. {{Lösung versteckt|1= Setze die Werte wie folgt in die Formel ein: <math>\frac{h(2,01) - h(1,99)}{2,01-1,99} = \frac{1,010025-0,990025}{2,01-1,99} = 0,02:0,02 = 1</math>. |2= Lösungsweg|3=Lösungsweg}} Da das Intervall sehr klein ist, nähern sich die Schnittpunkte der Sekante mit der Funktion und die durchschnittliche Änderungsrate geht in die lokale über.|2=Lösung|3=Lösung}} | {{Lösung versteckt|1 = Die durchschnittliche Änderung auf dem Intervall beträgt 1. {{Lösung versteckt|1= Setze die Werte wie folgt in die Formel ein: <math>\frac{h(2,01) - h(1,99)}{2,01-1,99} = \frac{1,010025-0,990025}{2,01-1,99} = 0,02:0,02 = 1</math>. |2= Lösungsweg|3=Lösungsweg}} Da das Intervall sehr klein ist, nähern sich die Schnittpunkte der Sekante mit der Funktion und die durchschnittliche Änderungsrate geht in die lokale über.|2=Lösung|3=Lösung}} | ||
|Farbe= {{Farbe|orange}} | |Farbe= {{Farbe|orange}} | ||
| Zeile 64: | Zeile 70: | ||
{{Box|1= <span style="color: orange"></span>Aufgabe 2: Übergang von durchschnittlicher zur | {{Box|1= <span style="color: orange"></span>Aufgabe 2: Übergang von durchschnittlicher zur lokalen Änderungsrate|2= Du benötigst für diese Aufgabe Papier und Stifte für Notizen. | ||
In dem Applet ist der Graph der Funktion <math>f(x)=0,1\cdot x^2 +1</math> dargestellt. | In dem Applet ist der Graph der Funktion <math>f(x)=0,1\cdot x^2 +1</math> dargestellt. | ||
Hinweis: GeoGebra verwendet bei Dezimalzahlen einen Punkt statt ein Komma, also <math> 0,1 </math> wird dort als <math> 0.1 </math> geschrieben. | |||
a) Verändere mithilfe des Schiebereglers für <math>\Delta x</math> den Abstand zwischen den Punkten <math>A </math> und <math> B </math> und notiere für | |||
{{Lösung versteckt|1 = Schiebe den Regler so weit, dass | <math> \Delta x = 3,5 ; \Delta x =3,0 ; \Delta x =2,5;\Delta x = 2,0; \Delta x =1,5; \Delta x =1,2; \Delta x = 1,1 </math> und <math> \Delta x =0,5 </math> die Steigung <math> k </math> der Sekanten durch die Punkte <math>A </math> und <math> B </math>. | ||
b) Kannst du damit die Steigung der Tangente, also die lokale Änderungsrate an einem Punkt ermitteln? | |||
{{Lösung versteckt|1 = Schiebe den Regler so weit, dass <math>\Delta x = 0 </math> ist. Die Schnittpunkte nähern sich also, die Sekante geht in die Tangente über und somit entsteht aus der durchschnittlichen Änderungsrate am Grenzübergang die lokale.|2= Tipp|3=Tipp}} | |||
c) Führe dieselbe Aufgabe für die Funktion <math>f(x) =0,1 \cdot x^2</math> durch. Was stellst du fest? Ist es überraschend? | |||
<ggb_applet id="KMv29tYV" width="100%" height="100%" border="888888" /> | <ggb_applet id="KMv29tYV" width="100%" height="100%" border="888888" /> | ||
{{Lösung versteckt|1 = Die Steigung der Tangenten beider Funktionen | {{Lösung versteckt|1 = Die Steigung der Tangenten beider Funktionen im Punkt <math> A </math> beträgt <math>m=0,6</math>. Die notierten Werte der durchschnittlichen Änderungsraten nähern sich dieser Zahl an, wenn sich <math>\Delta x</math> der Zahl 0 nähert. Das entspricht genau der Definition der Tangente als Grenzwert der Sekantensteigungen. Der gleiche Wert für die zweite Funktion sollte auch nicht überraschen, denn diese ist die gleiche Funktion, lediglich um 1 nach unten verschoben. |2=Lösung|3=Lösung}} |Farbe= {{Farbe|orange}} | ||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
| Zeile 83: | Zeile 92: | ||
[[Datei:Kinder auf einem Schlitten.JPG|links|rahmenlos]] | [[Datei:Kinder auf einem Schlitten.JPG|links|rahmenlos]] | ||
Im kalten Winter unter idealen | Im kalten Winter unter idealen Bedingungen (keine Reibung, kein hektisches Lenken und kein unnötiges Bremsen) schlitterst Du einen Hang mit 5 % Gefälle hinab. | ||
Der von deinem Schlitten zurückgelegte Weg wird annähernd durch die Funktion | Der von deinem Schlitten zurückgelegte Weg wird annähernd durch die Funktion | ||
| Zeile 91: | Zeile 100: | ||
'''''a) Wann fährst du an deinem Freund vorbei?''''' | '''''a) Wann fährst du an deinem Freund vorbei?''''' | ||
{{Lösung versteckt|1= Hier | {{Lösung versteckt|1= Hier kannst du mit dem Funtkionsterm arbeiten. Die Entfernung bis zu deinem Freund, also 100 ist der Wert der Funktion zum gesuchten Zeitpunkt <math>t</math>. Stelle mit Hilfe des Funktionsterms eine Gleichung auf, mit <math>t</math> als Variable. | ||
|2= Tipp|3=Tipp}} | |2= Tipp|3=Tipp}} | ||
| Zeile 100: | Zeile 109: | ||
<math>\Leftrightarrow</math><math>t= \pm 20</math> | <math>\Leftrightarrow</math><math>t= \pm 20</math> | ||
Den Wert t = -20 können wir in dem Sachzusammenhang verwerfen ( | Den Wert <math> t = -20 </math> können wir in dem Sachzusammenhang verwerfen (du sitzt schließlich auf dem Schlitten, nicht in der Zeitmaschine), also fährst du <math>20 s </math> später an deinem Freund vorbei.|2= Lösung|3= Lösung}} | ||
'''''b) Welche Geschwindgkeit hat dein Schlitten zu diesem Zeitpunkt?''''' | '''''b) Welche Geschwindgkeit hat dein Schlitten zu diesem Zeitpunkt?''''' | ||
{{Lösung versteckt|1= Die Geschwindigkeit wird als <math>\frac{Strecke}{Zeit}</math> berechnet. Die Geschwindigkeit steht also in dieser Aufgabe für die Änderungsrate. Überlege zuerst nach welcher Änderungsrate | {{Lösung versteckt|1= Die Geschwindigkeit wird als <math>\frac{Strecke}{Zeit}</math> berechnet. Die Geschwindigkeit steht also in dieser Aufgabe für die Änderungsrate. Überlege zuerst, nach welcher Änderungsrate hier gefragt wird. Die Begriffe Strecke oder Zeitabschnitt stehen für durchschnittliche Veränderungen, dagegen werden mit Begriffen wie "zum Zeitpunkt" oder "im Moment" lokale Änderungsrate bezeichnet.|2= Tipp|3=Tipp}} | ||
{{Lösung versteckt |1= Du fährst mit einer Geschwindigkeit von 10 m/ | {{Lösung versteckt |1= Du fährst mit einer Geschwindigkeit von <math> 10 \frac{m}{s} </math> an deinem Freund vorbei. Im Teil a) hast du berechnet, dass du nach <math> 20 s </math> an deinem Freund vorbei schlitterst. Es gibt nun 2 Möglichkeiten die Geschwindigkeit an dieser Stelle zu berechnen. {{Lösung versteckt|1= Berechne den Differentialquotient im <math>t= 20</math>. Die Formel dazu findest du im zweiten Merkkasten: | ||
<math>\lim_{h \to \ 0}\frac{f(x+h)-f(x)}{h}</math> | <math>\lim_{h \to \ 0}\frac{f(x+h)-f(x)}{h}</math> | ||
<math>\lim_{h \to \ 0}\frac{f(20+h)-f(20)}{h}</math> | <math>\lim_{h \to \ 0}\frac{f(20+h)-f(20)}{h}</math> | ||
<math>\lim_{h \to \ 0} \frac{\tfrac{1}{4}(20 + h)^2 - \tfrac{1}{4}\cdot 20^2}{h} = \lim_{h \to \ 0} \frac{100 + 10h + \tfrac{1}{4}h^2 - 100}{h} = \lim_{h \to \ 0} \frac{h (10 + \tfrac{1}{4}h)}{h} = \lim_{h \to \ 0} (10 + \tfrac{1}{4}h) = 10 \tfrac{m}{s}</math> Im letzten Rechenschritt | |||
<math>= \lim_{h \to \ 0} \frac{\tfrac{1}{4}(20 + h)^2 - \tfrac{1}{4}\cdot 20^2}{h} </math> | |||
<math>= \lim_{h \to \ 0} \frac{100 + 10h + \tfrac{1}{4}h^2 - 100}{h} </math> | |||
<math>= \lim_{h \to \ 0} \frac{h (10 + \tfrac{1}{4}h)}{h} </math> | |||
<math>= \lim_{h \to \ 0} (10 + \tfrac{1}{4}h) </math> | |||
<math>= 10 \tfrac{m}{s}</math> | |||
Im letzten Rechenschritt überlege, was mit dem Ausdruck <math>(10 + \tfrac{1}{4}h)</math> passiert, wenn <math>h = 0</math> ist.|2=Lösungsweg 1|3= Lösungsweg 1}} | |||
{{Lösung versteckt|1= Wenn du bereits die Potenzregel zur Berechnung der Ableitungen kennst, so kannst du die momentane Geschwindigkeit als Wert der Ableitung an dieser Stelle (hier für <math>t=20</math>) berechnen: | |||
<math>f'(20)= \tfrac{1}{4}\cdot2\cdot20 = 10</math>|2=Lösungsweg 2|3=Lösungsweg 2}} |2= Lösung|3= Lösung}} | <math>f'(20)= \tfrac{1}{4}\cdot2\cdot20 = 10</math>|2=Lösungsweg 2|3=Lösungsweg 2}} |2= Lösung|3= Lösung}} | ||
| Zeile 127: | Zeile 149: | ||
Gegeben sind die Funktionen: | Gegeben sind die Funktionen: | ||
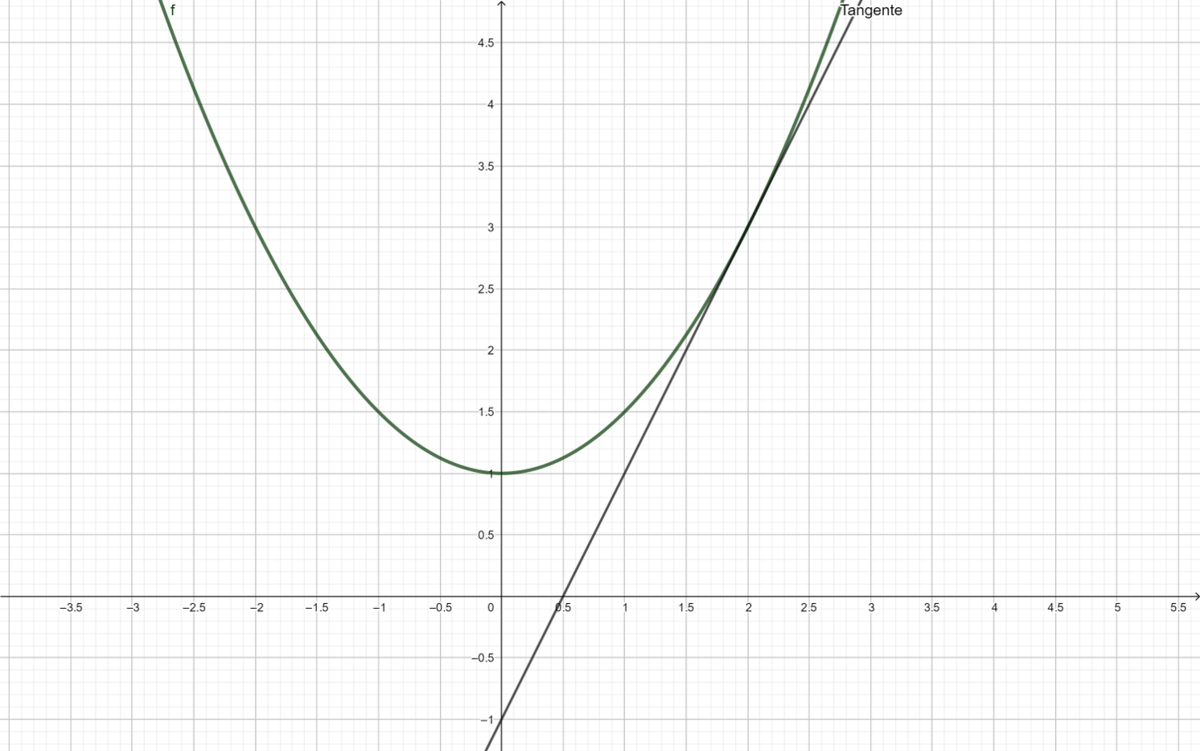
*<math>f(x)=\tfrac{1}{2}x^2+1</math> und der Punkt | *<math>f(x)=\tfrac{1}{2}x^2+1</math> und der Punkt <math> (2| f(2)) </math> | ||
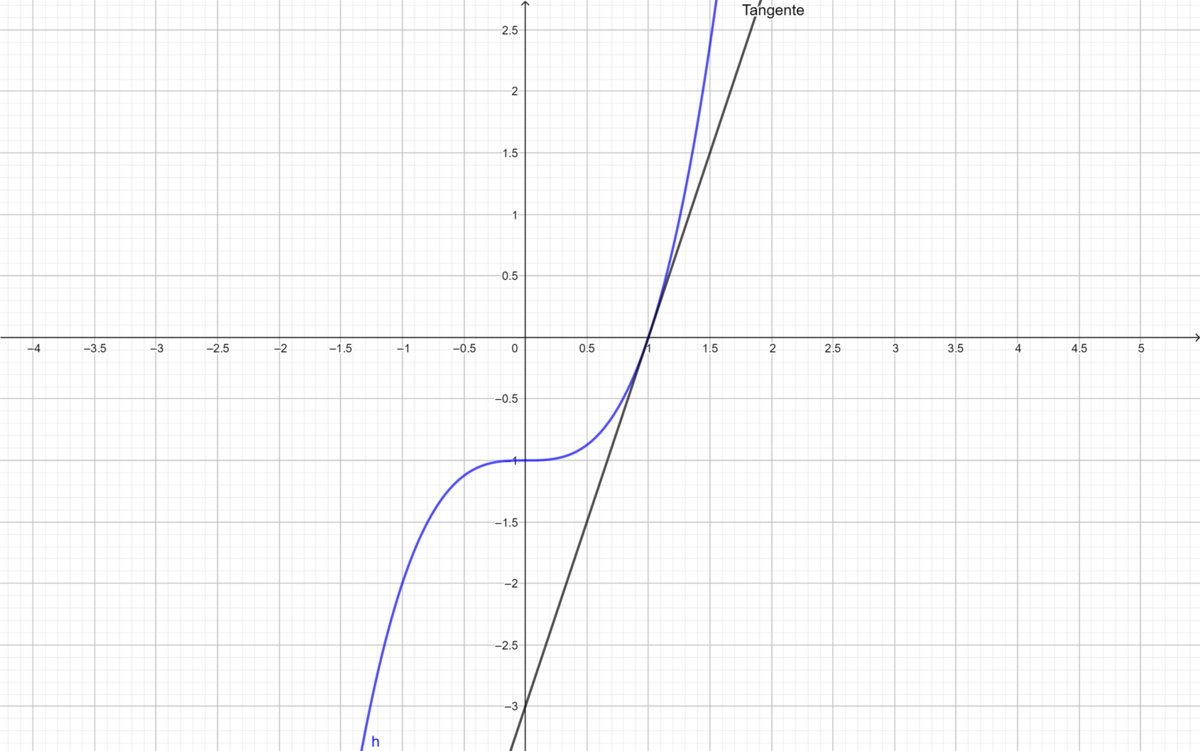
*<math>h(x)=x^3-1</math> und der Punkt | *<math>h(x)=x^3-1</math> und der Punkt <math> (1| h(1))</math>. | ||
'''''a) Zeichne die Graphen der Funktionen f(x) und h(x) und skizziere die Tangenten in den angegebenen Punkten. ''''' | '''''a) Zeichne die Graphen der Funktionen f(x) und h(x) und skizziere die Tangenten in den angegebenen Punkten. ''''' | ||
| Zeile 135: | Zeile 157: | ||
{{Lösung versteckt|1=[[Datei:Loesung 5a Funktion h.png|1200px|zentriert|rahmenlos]]|2=Skizze h(x)|3=Skizze h(x)}} | {{Lösung versteckt|1=[[Datei:Loesung 5a Funktion h.png|1200px|zentriert|rahmenlos]]|2=Skizze h(x)|3=Skizze h(x)}} | ||
'''''b)Bestimme die Steigung der Funktion im gegebenen Punkt durch Ablesen der Tangentensteigung.''''' | '''''b) Bestimme die Steigung der Funktion im gegebenen Punkt durch Ablesen der Tangentensteigung.''''' | ||
{{Lösung versteckt|1 = Erinnerst | {{Lösung versteckt|1 = Erinnerst du dich, dass die Steigung der Funktion in einem Punkt mit der Steigung der Tangente in diesem Punkt übereinstimmt? Für das Ablesen der Tangentensteigung suche dir am besten ein Intervall zwischen 2 benachbarten ganzen Zahlen, deren Funktionswerte gut abzulesen sind. Steigungsdreieck ist hier das Stichwort. |2=Tipp|3=Tipp}} | ||
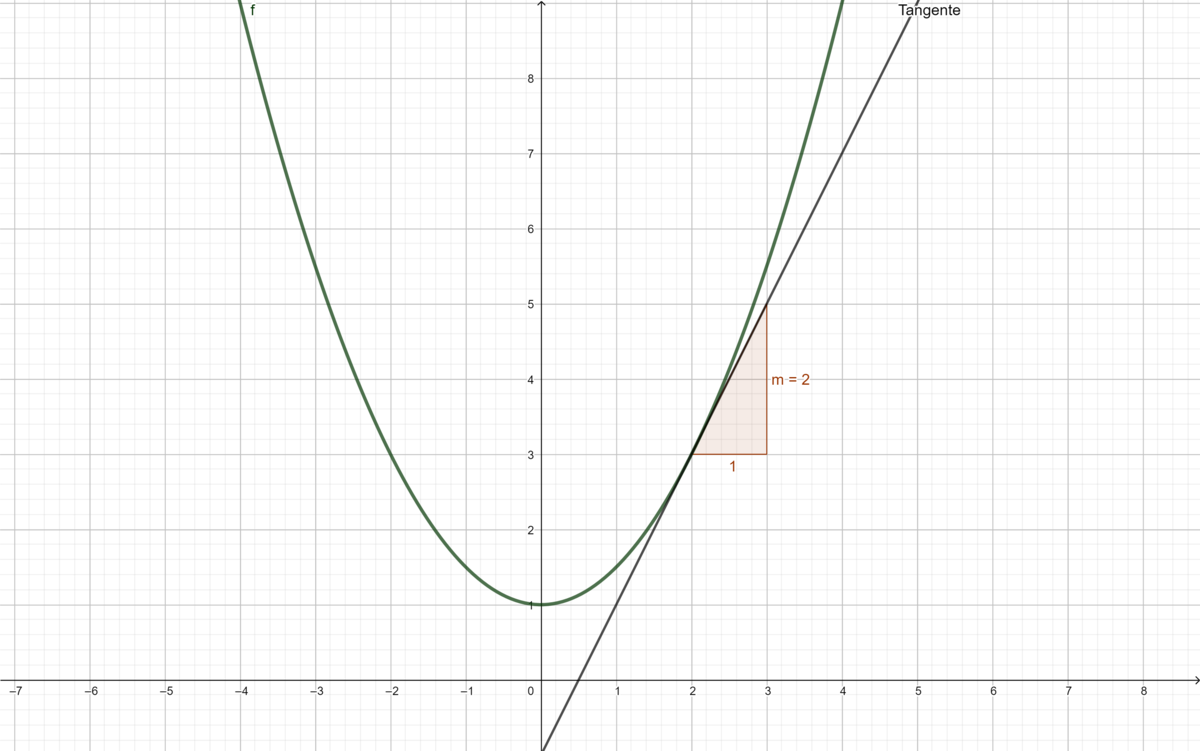
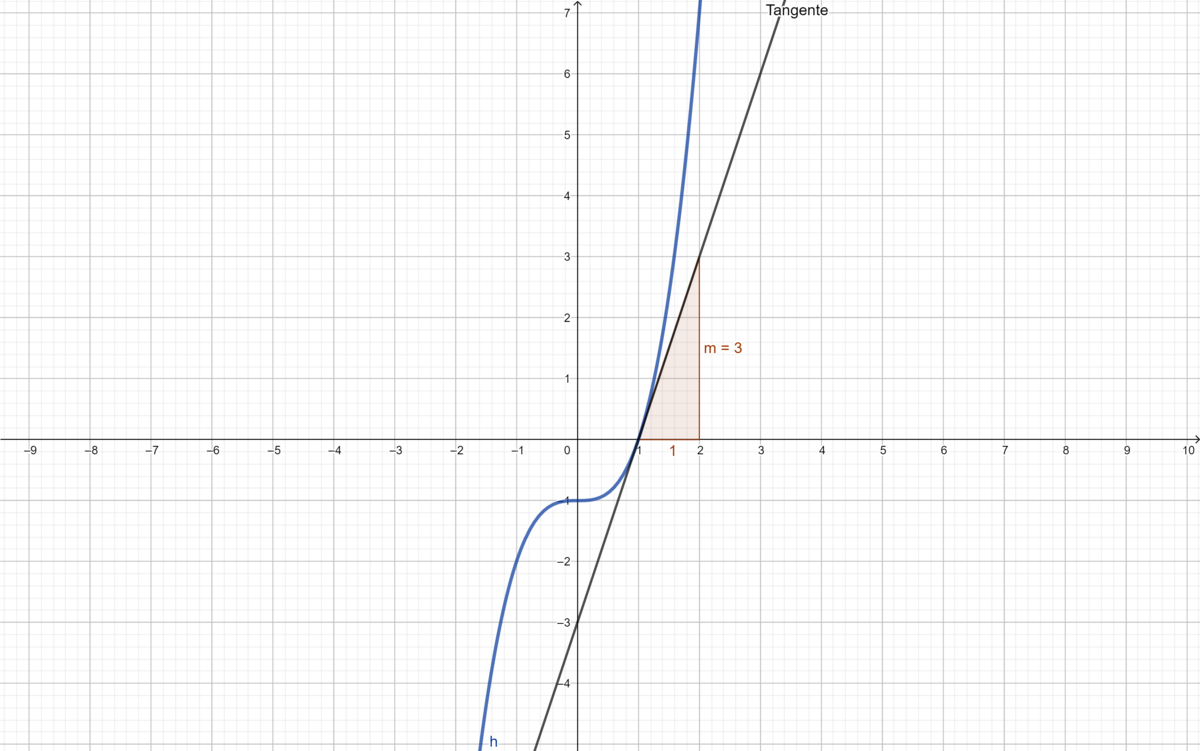
{{Lösung versteckt|1 = Die Tangente der Funktion <math>f(x)</math> hat an der vorgegebenen Stelle Steigung <math>m=2</math>. Die Tangente der Funktion <math>h(x)</math> hat an der Stelle 1 die Steigung <math>m=3</math> Wie komme ich zu meiner Lösung? Beide Steigungen sind am einfachsten im Intervall [1; 2] abzulesen | {{Lösung versteckt|1 = Die Tangente der Funktion <math>f(x)</math> hat an der vorgegebenen Stelle Steigung <math>m=2</math>. Die Tangente der Funktion <math>h(x)</math> hat an der Stelle 1 die Steigung <math>m=3</math> Wie komme ich zu meiner Lösung? Beide Steigungen sind am einfachsten im Intervall <math>[1; 2]</math> abzulesen | ||
{{Lösung versteckt|1=[[Datei:Steigungf.png|1200px|zentriert|rahmenlos]]|2=Steigungsdreieck für f(x)|3=Steigungsdreieck für f(x)}} | {{Lösung versteckt|1=[[Datei:Steigungf.png|1200px|zentriert|rahmenlos]]|2=Steigungsdreieck für f(x)|3=Steigungsdreieck für f(x)}} | ||
| Zeile 147: | Zeile 169: | ||
|2=Lösung|3=Lösung}} | |2=Lösung|3=Lösung}} | ||
'''''c) Bestimme rechnerisch die lokale Änderungsrate der jeweiligen Funktion im vorgegebenen Punkt. Vergleiche | '''''c) Bestimme rechnerisch die lokale Änderungsrate der jeweiligen Funktion im vorgegebenen Punkt. Vergleiche deine Ergebnisse mit den Ergebnissen aus Teil b).''''' | ||
{{Lösung versteckt|1 = Die lokale Änderungsrate im vorgegebenem Punkt berechnest Du am besten mit dieser Formel: <math>f'(x)=\lim_{h \to \ 0}\frac{f(x+h)-f(x)}{h}</math>. | {{Lösung versteckt|1 = Die lokale Änderungsrate im vorgegebenem Punkt berechnest Du am besten mit dieser Formel: <math>f'(x)=\lim_{h \to \ 0}\frac{f(x+h)-f(x)}{h}</math>. | ||
Hier entspricht die Steigung dem Wert der Ableitung an der vorgegebenen Stelle. | Hier entspricht die Steigung dem Wert der Ableitung an der vorgegebenen Stelle. | ||
Für die Funktion <math>f(x)</math> rechnest | Für die Funktion <math>f(x)</math> rechnest du also: | ||
<math>m= \lim_{h \to \ 0}\frac{\tfrac{1}{2}(2+h)^2+1-\tfrac{1}{2}\cdot2^2-1}{h} = \lim_{h \to \ 0}\frac{2 + 2h + 0,5h^2-2}{h}= \lim_{h \to \ 0}(2+0,5h) = 2</math> , wenn du <math>h=0</math> einsetzt. | <math>m= \lim_{h \to \ 0}\frac{\tfrac{1}{2}(2+h)^2+1-\tfrac{1}{2}\cdot2^2-1}{h} = \lim_{h \to \ 0}\frac{2 + 2h + 0,5h^2-2}{h}= \lim_{h \to \ 0}(2+0,5h) = 2</math> , wenn du <math>h=0</math> einsetzt. | ||
Für die Funktion <math>h(x)</math> rechnest | Für die Funktion <math>h(x)</math> rechnest du: | ||
<math>m=\lim_{h \to \ 0} \frac{(1+h)^3-1-1^3+1}{h} = \lim_{h \to \ 0} \frac{1+3h+3h^2+h^3-1}{h} = \lim_{h \to \ 0} (3+ 3h + h^2) = 3</math> | <math>m=\lim_{h \to \ 0} \frac{(1+h)^3-1-1^3+1}{h} = \lim_{h \to \ 0} \frac{1+3h+3h^2+h^3-1}{h} = \lim_{h \to \ 0} (3+ 3h + h^2) = 3</math> | ||
Wenn | Wenn du sauber gezeichnet und abgelesen hast, sind die Antworten in den Teilen b) und c) gleich. Die Steigung der Tangente einer Funktion ist also genau die lokale Änderungsrate der Funktion in der kleinsten Umgebung um den Berührungspunkt mit der Tangente. |2=Lösung|3=Lösung}} |3= Arbeitsmethode}} | ||
{{Box|1= <span style="color: blue"></span>Aufgabe 6: Anwendung in der Physik|2= Du benötigst für die Aufgabe Papier, Stifte und einen Taschenrechner. | {{Box|1= <span style="color: blue"></span>Aufgabe 6: Anwendung in der Physik|2= Du benötigst für die Aufgabe Papier, Stifte und einen Taschenrechner. | ||
[[Datei:Nagasaki 1945 - Before and after (adjusted).jpg|links | [[Datei:Nagasaki 1945 - Before and after (adjusted).jpg|mini|links|Nagasaki 1945 - vor und nach der atomaren Explosion]] | ||
Die Verbreitung der Schockwelle einer atomaren Explosion kann man annähernd mit folgender Funktion beschreiben: | Die Verbreitung der Schockwelle einer atomaren Explosion kann man annähernd mit folgender Funktion beschreiben: | ||
<math>R(t)=1,6t^2 + 3,2t</math> | <math>R(t)=1,6t^2 + 3,2t</math> | ||
| Zeile 171: | Zeile 193: | ||
* ersten drei Sekunden nach der Explosion | * ersten drei Sekunden nach der Explosion | ||
* ersten zehn Sekunden nach der Explosion | * ersten zehn Sekunden nach der Explosion | ||
* | * Im Zeitraum von 7 bis 10 Sekunden nach der Explosion. | ||
{{Lösung versteckt|1 = Die mittlere Ausbreitungsgeschwindigkeit ist genau die Veränderung (also die Steigung oder die Änderungsrate)der Funktion in einem Zeitabschnitt. Die Steigung der Funktion in einem Intervall wird als Differenzenquotient <math>\frac{\bigtriangleup R(t)}{\bigtriangleup t}</math> berechnet, also hier in diesem Fall als <math>\frac{Strecke}{Zeit}</math>|2=Tipp|3=Tipp}} | {{Lösung versteckt|1 = Die mittlere Ausbreitungsgeschwindigkeit ist genau die Veränderung (also die Steigung oder die Änderungsrate) der Funktion in einem Zeitabschnitt. Die Steigung der Funktion in einem Intervall wird als Differenzenquotient <math>\frac{\bigtriangleup R(t)}{\bigtriangleup t}</math> berechnet, also hier in diesem Fall als <math>\frac{Strecke}{Zeit}</math>|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1 = Im Teil a) wird nach dem Differenzenquotient gefragt, den | {{Lösung versteckt|1 = Im Teil a) wird nach dem Differenzenquotient gefragt, den du mit der Formel : <math>\frac{f(x_2) - f(x_1)}{x_2-x_1}</math> berechnest. | ||
Für die ersten 3 Sekunden heißt im Intervall [0; 3],somit: | Für die ersten 3 Sekunden heißt im Intervall <math>[0; 3]</math>,somit ergibt sich: | ||
<math>V= \frac{R(3)-R(0)}{3-0} = \frac{1,6\cdot(3^2) + 3,2\cdot3-0}{3} = \frac{24}{3} = 8</math> km/ | <math>V= \frac{R(3)-R(0)}{3-0} = \frac{1,6\cdot(3^2) + 3,2\cdot3-0}{3} = \frac{24}{3} = 8</math> <math>\frac{km}{s}</math>. | ||
Die Lösung für die ersten 10 Sekunden lautet : 19,2 km/ | Die Lösung für die ersten 10 Sekunden lautet : <math>19,2 \frac{km}{s}</math>. Im Zeitintervall zwischen der 7. und der 10. Sekunde beträgt die mittlere Ausbreitungsgeschwindigkeit <math>30,4 \frac{km}{s}</math>. | ||
|2=Lösung|3=Lösung}} | |2=Lösung|3=Lösung}} | ||
| Zeile 188: | Zeile 210: | ||
* zehnte Sekunde nach der Explosion | * zehnte Sekunde nach der Explosion | ||
{{Lösung versteckt|1 = | {{Lösung versteckt|1 = Hier ist nach der momentanen Geschwindigkeit gefragt. Stelle dir also die Frage, ob es um die durchschnittliche oder lokale Änderungsrate der Funktion geht. Vergleiche mit dem Teil a). Die entsprechende Berechnungsformeln findest du in Merkkästen am Anfang des Kapitels.|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1 = Wird nach der Geschwindigkeit zu einem Zeitpunkt bei einer Weg-Zeit-Funktion gefragt, so handelt es sich um die lokale Änderungsrate | {{Lösung versteckt|1 = Wird nach der Geschwindigkeit zu einem Zeitpunkt bei einer Weg-Zeit-Funktion gefragt, so handelt es sich um die lokale Änderungsrate. Der Differntialquotient ist also geeignet. | ||
Für die Geschwindigkeit in der zweiten Sekunde rechnest Du also: | Für die Geschwindigkeit in der zweiten Sekunde rechnest Du also: | ||
<math>R'(2)=\lim_{h \to \ 0}\frac{R(2+h)-R(2)}{h}</math> <math>=\lim_{h \to \ 0} \frac{1,6 (2+h)^2+3,2\cdot(2+h)-1,6\cdot4-3,2\cdot2}{h} =\lim_{h \to \ 0} (6,4 + 1,6h +3,2) = 8,6</math> km/ | <math>R'(2)=\lim_{h \to \ 0}\frac{R(2+h)-R(2)}{h}</math> <math>=\lim_{h \to \ 0} \frac{1,6 (2+h)^2+3,2\cdot(2+h)-1,6\cdot4-3,2\cdot2}{h} =\lim_{h \to \ 0} (6,4 + 1,6h +3,2) = 8,6</math> <math> \frac{km}{s} </math>. | ||
Die momentane Ausbreitungsgeschwindigkeit in der Sekunde 10 beträgt bereits | Die momentane Ausbreitungsgeschwindigkeit in der Sekunde 10 beträgt bereits <math> 35,2 \frac{km}{s} </math>. | ||
|2=Lösung|3=Lösung}} | |2=Lösung|3=Lösung}} | ||
| Zeile 202: | Zeile 224: | ||
{{LearningApp|app=10938377|width=100%|height=600px}} | {{LearningApp|app=10938377|width=100%|height=600px}} | ||
{{Lösung versteckt|1= Überlege zuerst welche Begriffe | {{Lösung versteckt|1= Überlege zuerst, welche Begriffe dem <math>x</math>-Wert und dem <math>y</math>-Wert zuzuordnen sind. Was hängt also wie von einander ab? | ||
Zum Beispiel hängt die zurückgelegte Strecke von der Fahrzeit ab. Damit kann schon einmal die Funktion beschrieben werden. Die Formeln für durchschnittliche und momentane (lokale) Änderungsraten findest du in den Merkkästen. |2=Tipp|3=Tipp}} | |||
|3= Arbeitsmethode}} | |3= Arbeitsmethode}} | ||
| Zeile 213: | Zeile 237: | ||
Ein Teil der Achterbahn lässt sich durch den Graphen der Funktion: <math>f(x) = \tfrac{1}{4}x^2 + 1</math> beschreiben. | Ein Teil der Achterbahn lässt sich durch den Graphen der Funktion: <math>f(x) = \tfrac{1}{4}x^2 + 1</math> beschreiben. | ||
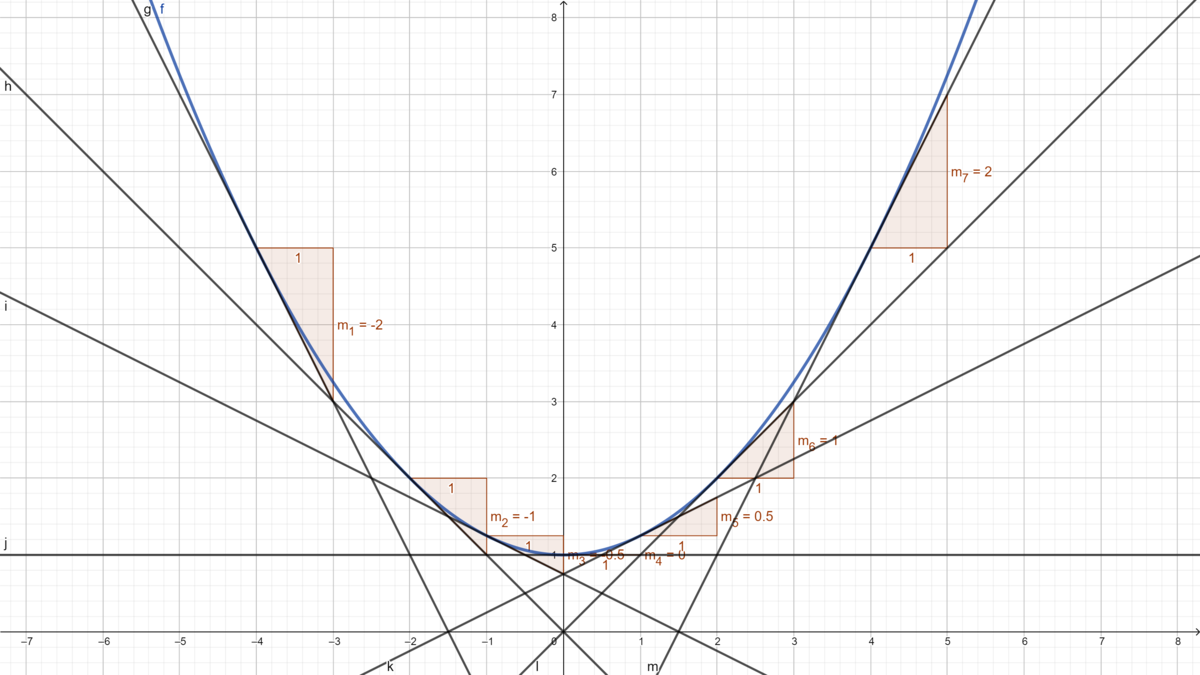
''''' | '''a)''' Zeichne den Graphen der Funktion <math>f(x)</math>. Notiere folgende Tabelle auf einem Blatt Papier und vervollständige sie, indem du an den angegebenen Stellen die Tangenten skizzierst und deren Steigungen <math>m</math> durch Ablesen bestimmst. | ||
[[Datei:Tabelle 1.png|550 px|zentriert|rahmenlos|mini]] | [[Datei:Tabelle 1.png|550 px|zentriert|rahmenlos|mini]] | ||
| Zeile 223: | Zeile 247: | ||
'''b)''' Da es zu jedem Punkt nur eine Tangente gibt, ist die Zuordnung <math>m \longmapsto x</math> eine Funktion <math>m(x)</math> | '''b)''' Da es zu jedem Punkt nur eine Tangente gibt, ist die Zuordnung <math>m \longmapsto x</math> eine Funktion <math>m(x).</math> Betrachte die Wertepaare in der Tabelle bei Teil a). Die Funktion gibt für jeden Wegpunkt der Achterbahn an, ob diese hoch- oder runterfährt und wie steil die jeweiligen Steigungen sind. | ||
'''''c) Berechne den | Stelle die Gleichung der Funktion <math> m(x) </math> auf und zeichne diese in dein Koordinatensystem. | ||
{{Lösung versteckt|1 = | {{Lösung versteckt|1= Für alle Wertepaare gilt, dass der Wert <math>m</math> ein Vielfaches von <math>x</math> ist, wobei dieser Faktor eine feste Zahl ist. Solche Zuordnungen nennt man linear.|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1 = Die Funktionsgleichung lautet: <math>m(x) = \tfrac{1}{2} x</math>. Denn <math>-1 = 0,5 \cdot (-2)</math> oder <math>1,5 = 0,5\cdot 3</math>. Diese Funktion gibt die lokale Steigungsänderung der Achterbahn in Abhängigkeit vom Streckenpunkt an. Das hast du beim Skizzieren der Tangenten sicherlich bereits vermutet. Da die '''lokalen''' Änderungsraten bestimmt wurden, ist diese Funktion die Ableitungsfunktion von <math>f(x)</math>. Dieses Verfahren nennt man graphisches Differenzieren. Im Teil c) kannst du diese Behauptung rechnerisch überprüfen.|2= Lösung|3=Lösung}} | |||
'''c)''' Wie steil ist die Steigung der Achterbahn an einer von dir gewählten Stelle und fährt sie an dieser auf- oder abwärts? Gebe eine Funktion an, die die Steigung an einer beliebigen Stelle berechnet und vergleiche dein Ergebnis mit dem Ergebnis von Teil b). | |||
{{Lösung versteckt|1= Berechne den Differentialquotienten von <math>f(x) = \tfrac{1}{4} x^2 + 1</math> in einem beliebigen Punkt. |2=Tipp|3=Tipp}} | |||
{{Lösung versteckt|1 = Der Differentialquotient lässt sich wie folgt berechnen: <math>f'(x) = \lim_{h \to \ 0} \frac{f(x +h) - f(x)}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}(x +h)^2 + 1 - \tfrac{1}{4}x^2-1}{h} = \lim_{h \to \ 0} \frac{\tfrac{1}{4}x^2 +\tfrac{1}{2} xh+\tfrac{1}{4} h^2- \tfrac{1}{4}x^2}{h} = \lim_{h \to \ 0} ( \tfrac{1}{2}x + \tfrac{1}{4}h) = \tfrac{1}{2}x </math>. | |||
Das ist die gleiche Funktion wie beim graphischen Differenzieren im Teil b. Die Ableitung ist also die Steigung der Tangente der Funktion in einem bestimmtem Punkt. In diesem Fall kannst du damit die Steigung der Achterbahn, sowie ob diese auf oder abfährt an jedem Streckenpunkt schnell berechnen. |2=Lösung|3=Lösung}}|Farbe = {{Farbe|grün|dunkel}} |3= Arbeitsmethode}} | |||
{{Box|1= <span style="color: green"></span> ⭐Aufgabe 9: Tangenten für Funktionenschar |2= Du benötigst für die Aufgabe Papier, Stifte, Lineal und evtl. einen Taschenrechner. | {{Box|1= <span style="color: green"></span> ⭐Aufgabe 9: Tangenten für Funktionenschar |2= Du benötigst für die Aufgabe Papier, Stifte, Lineal und evtl. einen Taschenrechner. | ||
Gegeben ist eine Funktionenschar durch die Gleichung <math>f_t(x) = x^3 - 3t^2x </math> | Gegeben ist eine Funktionenschar durch die Gleichung <math>f_t(x) = x^3 - 3t^2x </math> mit <math>t>0</math> | ||
''''' | '''a)''' Für welches <math>t</math> ist <math> T(x) = -x </math> | ||
die Tangente im Ursprung? | die Tangente im Ursprung? | ||
{{Lösung versteckt|1 = 1)Berechne den Wert der ersten Ableitung der | {{Lösung versteckt|1 = Die Tangente im Ursprung hat die Vorschrift <math>T(x) = mx</math>. Überlege, was die Steigung der Tangente <math>m</math> mit der Änderungsrate und der Ableitung zu tun haben. Du suchst eine Tangente mit der Steigung <math>m=-1</math>.|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1 = 1) Berechne den Wert der ersten Ableitung der Funktionenschar an der Stelle <math>x=0</math>: | |||
<math>m= f' (0) = -3t^2</math>. | <math>m= f' (0) = -3t^2</math>. | ||
Also haben die Tangenten durch Ursprung die Formel <math>T_t(x) = -3t^2x</math> mit den Steigungen <math>m_t = -3t^2</math>. | Also haben die Tangenten durch den Ursprung die Formel <math>T_t(x) = -3t^2x</math> mit den Steigungen <math>m_t = -3t^2</math>. | ||
2) Wir suchen die Tangente <math>T_t(x)</math> mit der Steigung <math>m=-1</math>: | |||
<math>- 1 = -3t^2</math> | <math>- 1 = -3t^2</math> | ||
<math>\Leftrightarrow</math><math>t= \sqrt{\tfrac{1}{3}}</math> | |||
<math>\Leftrightarrow</math><math>t=\pm\sqrt{\tfrac{1}{3}}</math> | |||
3)Berücksichtige, dass laut der Aufgabe t>0 gilt. Somit ist für <math>f_\sqrt{\left ( \frac{1}{3} \right )}(x)=x^3-x</math> die Tangente im Ursprung | 3) Berücksichtige, dass laut der Aufgabe <math>t>0</math> gilt. Somit ist für <math>f_\sqrt{\left ( \frac{1}{3} \right )}(x)=x^3-x</math> die Tangente im Ursprung <math>T(x) = -x </math>. Diese Funktion ist blau gefärbt. | ||
[[Datei:Geogebra-exportfunktionenshar.png|1200px|zentriert|rahmenlos]] | [[Datei:Geogebra-exportfunktionenshar.png|1200px|zentriert|rahmenlos]] | ||
|2= Lösung|3=Lösung}} | |2= Lösung|3=Lösung}} | ||
''''' | '''b)''' Untersuche, an welchen Stellen die Funktionen der Schar eine waagerechte Tangente haben. | ||
{{Lösung versteckt|1 = Für waagerechte Tangenten gilt | {{Lösung versteckt|1 = Für waagerechte Tangenten gilt, dass die Steigung 0 ist. Die Steigung der Tangenten ist der Wert der Ableitung an dieser Stelle. Du suchst hier also, für welche Werte von <math>x</math> in Abhängigkeit von <math>t</math> gilt: <math>f_t'(x) = 0</math> . | ||
|2= Tipp|3=Tipp}} | |2= Tipp|3=Tipp}} | ||
| Zeile 272: | Zeile 301: | ||
<math>\Leftrightarrow</math><math> x = \pm t</math> | <math>\Leftrightarrow</math><math> x = \pm t</math> | ||
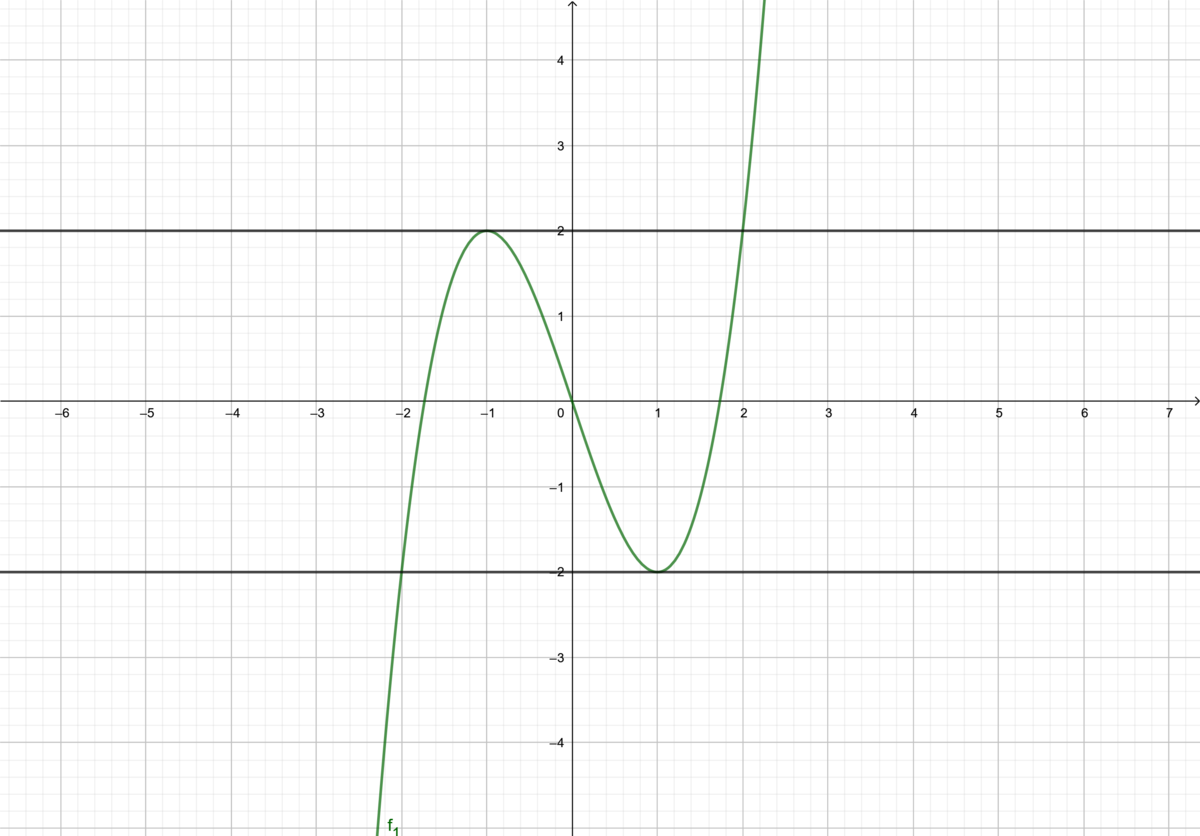
An den Stellen x = t und x = -t haben die Funktionen der Schar eine waagerechte Tangente. Zum Beispiel hat <math>f_1</math> an den Stellen 1 und -1 waagerechte Tangenten. | An den Stellen <math>x = t </math> und <math>x = -t </math> haben die Funktionen der Schar eine waagerechte Tangente. Zum Beispiel hat <math>f_1</math> an den Stellen 1 und -1 waagerechte Tangenten. | ||
[[Datei:Geogebra-exportfunktionenshar1.png|1200px|zentriert|rahmenlos]] | [[Datei:Geogebra-exportfunktionenshar1.png|1200px|zentriert|rahmenlos]] | ||
|2= Lösung|3=Lösung}} | |2= Lösung|3=Lösung}} | ||
|Farbe = {{Farbe|grün|dunkel}} |3= Arbeitsmethode}} | |Farbe = {{Farbe|grün|dunkel}} |3= Arbeitsmethode}} | ||
Aktuelle Version vom 12. Juni 2020, 22:48 Uhr
Grundlegende Begriffe und Formeln
Aufgaben zum Wiederholen und Vertiefen
Mittelschwere Aufgaben
Knobelaufgaben