Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (19 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
{{Box |1= Aufgabe 1 - Wendepunkte angeben | {{Box |1= Aufgabe 1 - Wendepunkte angeben | ||
|2= Gib in der Grafik an, ob an | |2= Gib in der Grafik an, ob an den markierten Punkten jeweils ein Wendepunkt vorliegt oder nicht. | ||
{{LearningApp|width:80%|height:450px|app=pasf50isa20}}|3=Arbeitsmethode| Farbe={{Farbe|orange}}}} | {{LearningApp|width:80%|height:450px|app=pasf50isa20}}|3=Arbeitsmethode| Farbe={{Farbe|orange}}}} | ||
{{Box | Merke: Lokales Extremum der Ableitung | {{Box | Merke: Lokales Extremum der Ableitung | ||
|An einem '''Wendepunkt''' einer Funktion <math>f(x)</math> ist die '''Steigung''' in der näheren Umgebung '''maximal bzw. minimal'''. Somit folgt, dass die Ableitung an dieser Stelle ein lokales Extremum aufweist. Daraus ergibt sich das notwendige Kriterium für einen Wendepunkt. Wenn die Funktion <math>f'(x)</math> | |An einem '''Wendepunkt''' einer Funktion <math>f(x)</math> ist die '''Steigung''' in der näheren Umgebung '''maximal bzw. minimal'''. Somit folgt, dass die Ableitung an dieser Stelle ein lokales Extremum aufweist. Daraus ergibt sich das notwendige Kriterium für einen Wendepunkt. Wenn die Funktion <math>f'(x)</math> an der Stelle <math> x_W </math> ein Extremum aufweist, so ist die Ableitung dieser Funktion an der Stelle gleich 0: <math>f''(x_W)=0</math> (Hinweis: Dies wurde im vorherigen Kapitel "Extema" bearbeitet). | ||
'''Zusammenfassung:''' | '''Zusammenfassung:''' | ||
* '''notwendiges Kriterium:''' <math>f''(x_W)=0</math> | * '''notwendiges Kriterium:''' <math>f''(x_W)=0</math> | ||
* '''hinreichendes Kriterium:''' <math>f'''(x_W) \neq 0</math>, ''' | * '''hinreichendes Kriterium:''' <math>f''(x_W)=0</math> und <math>f'''(x_W) \neq 0</math>, '''wobei gilt:''' <math>f'''(x_W) > 0 \Rightarrow</math>RLW oder <math>f'''(x_W) < 0 \Rightarrow</math>LRW | ||
| Merksatz}} | | Merksatz}} | ||
{{Box|Berechnung eines Wendepunktes| | {{Box|Verfahren zur Berechnung eines Wendepunktes| | ||
* '''Notwendiges Kriterium:''' Nullstellen <math> x_W </math> der zweiten Ableitung berechnen | * '''Notwendiges Kriterium:''' Nullstellen <math> x_W </math> der zweiten Ableitung berechnen | ||
* '''Hinreichendes Kriterium:''' Einsetzen der berechneten | * '''Hinreichendes Kriterium:''' Einsetzen der berechneten Wendestelle <math> x_W </math> in die dritte Ableitung (RLW oder LRW?) | ||
* '''Berechnen des Funktionswertes''' durch | * '''Berechnen des Funktionswertes''' durch Einsetzen der Wendestelle <math> x_W </math> in die ursprüngliche Funktion | ||
Du kannst dir noch gerne das folgende Beispiel anschauen: | Du kannst dir noch gerne das folgende Beispiel anschauen: | ||
| Zeile 50: | Zeile 50: | ||
* '''Hinreichendes Kriterium:''' <math>f'''(x_W)\neq 0</math> | * '''Hinreichendes Kriterium:''' <math>f''(x_W)=0</math> und <math>f'''(x_W)\neq 0</math> | ||
<math>f'''(x_{W_{1}})\approx 16{,}73>0</math> und <math>f'''(x_{W_{2}})\approx-16{,}73<0</math> | <math>f'''(x_{W_{1}})\approx 16{,}73>0</math> und <math>f'''(x_{W_{2}})\approx-16{,}73<0</math> | ||
| Zeile 63: | Zeile 63: | ||
<math>f(x_{W_{2}})=\frac{7}{12}\cdot (-\sqrt{\frac{10}{7}})^4-5\cdot (-\sqrt{\frac{10}{7}})^2\approx -5{,}95</math> | <math>f(x_{W_{2}})=\frac{7}{12}\cdot (-\sqrt{\frac{10}{7}})^4-5\cdot (-\sqrt{\frac{10}{7}})^2\approx -5{,}95</math> | ||
'''Lösung:''' An dem Punkt <math>(20|-5,95)</math> liegt | '''Lösung:''' An dem Punkt <math>(20|-5{,}95)</math> liegt ein Rechts-links-Wendepunkt vor und an dem Punkt <math>(-20|-5{,}95)</math> liegt ein Links-rechts-Wendepunkt vor. | ||
| Beispiel anzeigen |Beispiel verbergen}} | | Beispiel anzeigen |Beispiel verbergen}} | ||
| | | Merksatz}} | ||
| Zeile 75: | Zeile 75: | ||
{{Lösung versteckt|Schaue dir das obige Beispiel nochmal genau an!| Tipp 1 |Tipp verbergen}} | {{Lösung versteckt|Schaue dir das obige Beispiel nochmal genau an!| Tipp 1 |Tipp verbergen}} | ||
{{Lösung versteckt|Versuche, die drei Ableitungen von der Funktion zu berechnen und schaue dir dann die Kriterien für einen Wendepunkt an!| Tipp 2 |Tipp verbergen}} | {{Lösung versteckt|Versuche, die drei Ableitungen von der Funktion zu berechnen und schaue dir dann die Kriterien für einen Wendepunkt an!| Tipp 2 |Tipp verbergen}} | ||
{{Lösung versteckt|Um die Nullstelle eine Polynoms dritten Grades zu berechnen, kannst du ein <math>x</math> ausklammern.| Tipp 3| Tipp verbergen}} | {{Lösung versteckt|Um die Nullstelle eine Polynoms dritten Grades zu berechnen, kannst du hier ein <math>x</math> ausklammern.| Tipp 3| Tipp verbergen}} | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | ||
| Zeile 122: | Zeile 122: | ||
<math> g(x_{W_{1}}) = \frac{2}{25}\cdot 0^5-0^3+\frac{25}{8}\cdot 0=0 </math> | <math> g(x_{W_{1}}) = \frac{2}{25}\cdot 0^5-0^3+\frac{25}{8}\cdot 0=0 </math> | ||
<math> g(x_{W_{2}}) = \frac{2}{25}\cdot (\sqrt{\frac{15}{4}})^5-(\sqrt{\frac{15}{4}})^3+\frac{25}{8}\cdot \sqrt{\frac{15}{4}}\approx 0,97</math> | <math> g(x_{W_{2}}) = \frac{2}{25}\cdot (\sqrt{\frac{15}{4}})^5-(\sqrt{\frac{15}{4}})^3+\frac{25}{8}\cdot \sqrt{\frac{15}{4}}\approx 0{,}97</math> | ||
<math> g(x_{W_{3}}) = \frac{2}{25}\cdot (-\sqrt{\frac{15}{4}})^5-(-\sqrt{\frac{15}{4}})^3+\frac{25}{8}\cdot \sqrt{-\frac{15}{4}}\approx -0,97 </math> | <math> g(x_{W_{3}}) = \frac{2}{25}\cdot (-\sqrt{\frac{15}{4}})^5-(-\sqrt{\frac{15}{4}})^3+\frac{25}{8}\cdot \sqrt{-\frac{15}{4}}\approx -0{,}97 </math> | ||
| Rechenweg anzeigen |Rechenweg verbergen}} | | Rechenweg anzeigen |Rechenweg verbergen}} | ||
'''Lösung:''' An dem Punkt <math>(0 | '''Lösung:''' An dem Punkt <math>(0|0)</math> liegt ein Links-rechts-Wendepunkt vor und an den Punkten <math>(\sqrt{\frac{15}{4}}|0{,}97)</math> und <math>(-\sqrt{\frac{15}{4}}|-0{,}97)</math> liegen Rechts-links-Wendepunkte vor. | ||
| Lösung anzeigen |Lösung verbergen}} | | Lösung anzeigen |Lösung verbergen}} | ||
| Zeile 138: | Zeile 138: | ||
Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
<math> h'(x) = 3x^2-ax</math> | <math> h'(x) = 3x^2-ax</math> | ||
| Zeile 145: | Zeile 143: | ||
<math> h'''(x) = 6</math> | <math> h'''(x) = 6</math> | ||
* '''Notwendiges Kriterium:''' <math>h''(x_W)=0</math> | |||
<math> h''(x_{W}) = 6x_W-a =0 </math> | <math> h''(x_{W}) = 6x_W-a =0 </math> | ||
<math>\Rightarrow x_{W}=\frac{a}{6} </math> | <math>\Rightarrow x_{W}=\frac{a}{6} </math> | ||
| Zeile 167: | Zeile 168: | ||
| Rechenweg anzeigen |Rechenweg verbergen}} | | Rechenweg anzeigen |Rechenweg verbergen}} | ||
'''Lösung:''' Die Rechts-links- | '''Lösung:''' Die Rechts-links-Wendepunkte der Funktion der Schar liegen an den Punkten: <math>(\frac{a}{6}|-\frac{2}{6^3}a^3-a) </math>. | ||
| Lösung anzeigen |Lösung verbergen}} | | Lösung anzeigen |Lösung verbergen}} | ||
| Zeile 176: | Zeile 177: | ||
|2= | |2= | ||
[[File:Colossos Heide Park Soltau Germany.jpg|thumb|Achterbahn]] | [[File:Colossos Heide Park Soltau Germany.jpg|thumb|Achterbahn]] | ||
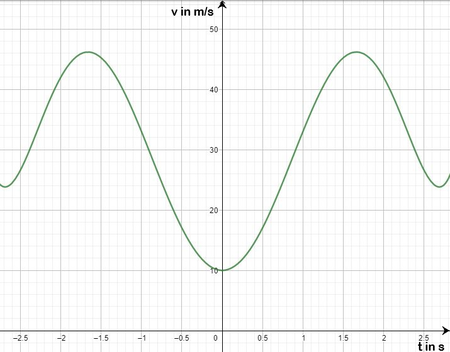
Im Europa Park in Baden-Württemberg soll eine schnelle Achterbahn gebaut werden. Kurz vor Schluss soll die Bahn über zwei hohe Punkte fahren und dort die Höchstgeschwindigkeiten erreichen. Die Mitarbeiter des Parks haben eine Simulation der Achterbahn erstellt und haben somit die Geschwindigkeit der Achterbahn gegen die Zeit aufgenommen. Die Funktion <math>v(t)=\frac{1}{2}t^6-\frac{15}{2}t^4+30t^{2}+10 </math> (siehe Abbildung) beschreibt im Intervall [-3,3] sehr gut die Geschwindigkeit der Achterbahn am Ende der Fahrt. | Im Europa Park in Baden-Württemberg soll eine schnelle Achterbahn gebaut werden. Kurz vor Schluss soll die Bahn über zwei hohe Punkte fahren und dort die Höchstgeschwindigkeiten erreichen. Die Mitarbeiter des Parks haben eine Simulation der Achterbahn erstellt und haben somit die Geschwindigkeit der Achterbahn gegen die Zeit in Sekunden aufgenommen. Die Funktion <math>v(t)=\frac{1}{2}t^6-\frac{15}{2}t^4+30t^{2}+10 </math> (siehe Abbildung) beschreibt im Intervall <math>[-3, 3]</math> Sekunden sehr gut die Geschwindigkeit der Achterbahn am Ende der Fahrt, wobei <math>t</math> für die Zeit und <math>s</math> für die Sekunden der Fahrt steht. Zum Zeitpunkt <math>t=0</math> schießt eine Kamera ein Foto von den Passagieren. | ||
| Zeile 186: | Zeile 187: | ||
Die Zeitpunkte, an denen die Achterbahn stark abbremst oder beschleunigt, sind sicherheitsrelevanten Momente der Fahrt. Zu diesen Zeitpunkten sollen deshalb besondere Sicherheitssysteme arbeiten. Zu welchen Zeitpunkten ist die Beschleunigung minimal bzw. maximal? '''Beachte:''' Es ist nur der '''Zeitpunkt''' gesucht, du musst also nicht den Funktionswert bzw. die Geschwindigkeit berechnen. Der letzte Schritt aus dem obigen Beispiel bleibt also aus. | |||
{{Lösung versteckt|Die Beschleunigung <math>a(t)</math> kann man | {{Lösung versteckt|Die Beschleunigung <math>a(t)</math> kann man berechnen, da sie der Ableitung der Geschwindigkeit entspricht also: <math>a(t)=v'(t)</math>. Die Geschwindigkeit ist angegeben. Was gilt für die Punkte, an denen die Beschleunigung maximal oder minimal ist? Lösung zu der Frage findest du in Tipp 2.| Tipp 1 anzeigen |Tipp verbergen}} | ||
{{Lösung versteckt|Zu dem Zeitpunkt <math>t_{W}</math>, an dem die Beschleunigung maximal bzw. minimal ist gilt: <math>a'(t_{W})=0</math>, da zu diesem Zeitpunkt die Beschleunigung eine Extremstelle und somit die Geschwindigkeit einen Wendepunkt aufweist. | {{Lösung versteckt|Zu dem Zeitpunkt <math>t_{W}</math>, an dem die Beschleunigung maximal bzw. minimal ist gilt: <math>a'(t_{W})=0</math>, da zu diesem Zeitpunkt die Beschleunigung eine Extremstelle und somit die Geschwindigkeit einen Wendepunkt aufweist. | ||
Hier soll also nur wieder der Wendepunkt berechnet werden. | Hier soll also nur wieder der Wendepunkt berechnet werden. Für weitere Tipps kannst du in der Aufgabe 2 und dem Beispiel schauen!| Tipp 2 anzeigen |Tipp verbergen}} | ||
{{Lösung versteckt|Eine Substitution:<math> t_{W}^2= z </math> ist zur | {{Lösung versteckt|Eine Substitution: <math> t_{W}^2= z </math> ist zur Berechnung der Nullstellen der zweiten Ableitung möglich!| Tipp 3 anzeigen |Tipp verbergen}} | ||
{{Lösung versteckt|Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | {{Lösung versteckt|Schaue dir hier die Rechnung an um den Lösungsweg schrittweise nachzuvollziehen! | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
<math> v(t)=\frac{1}{2}t^6-\frac{15}{2}t^4+30t^{2}+10 </math> | <math> v(t)=\frac{1}{2}t^6-\frac{15}{2}t^4+30t^{2}+10 </math> | ||
| Zeile 202: | Zeile 202: | ||
<math>v'''(t)=a''(t)=60t^3-180t </math> | <math>v'''(t)=a''(t)=60t^3-180t </math> | ||
<math>\Rightarrow 0=15z^2-90z+60</math> Die Gleichung | * '''Notwendiges Kriterium:''' <math>v''(t_{W})=a'(t_{W})=0</math>, wobei <math>a(t)</math> die Beschleunigung der Bahn beschreibt. | ||
<math>0=v''(t_{W})=a'(t_{W})=15t_{W}^4-90t_{W}^2+60</math> Substitution: <math> t_{W}^2= z </math> | |||
<math>\Rightarrow 0=15z^2-90z+60</math> Die Gleichung kann in die Form <math>x^2+px+q</math> gebracht werden, um die pq-Formel anzuwenden. | |||
<math>\Rightarrow 0=z^2-6z+4</math> pq-Formel anwenden mit <math>p=-6</math> und <math>q=4</math> | <math>\Rightarrow 0=z^2-6z+4</math> pq-Formel anwenden mit <math>p=-6</math> und <math>q=4</math> | ||
| Zeile 216: | Zeile 219: | ||
<math>\Rightarrow t_{W_{1/2}}=\pm \sqrt{3 + \sqrt {5}}</math> und <math>\Rightarrow t_{W_{3/4}}=\pm \sqrt{3 - \sqrt {5}}</math> | <math>\Rightarrow t_{W_{1/2}}=\pm \sqrt{3 + \sqrt {5}}</math> und <math>\Rightarrow t_{W_{3/4}}=\pm \sqrt{3 - \sqrt {5}}</math> | ||
<math>\Rightarrow t_{W_{1}}=\sqrt{3 + \sqrt {5}}</math>, <math> | <math>\Rightarrow t_{W_{1}}=\sqrt{3 + \sqrt {5}} \approx 2{,}29</math>, | ||
<math>t_{W_{2}}=-\sqrt{3 + \sqrt {5}} \approx -2{,}29</math>, | |||
<math>t_{W_{3}}=\sqrt{3 - \sqrt {5}} \approx 0{,}87</math> und | |||
<math>t_{W_{4}}=-\sqrt{3 - \sqrt {5}} \approx -0{,}87</math>. | |||
| Zeile 224: | Zeile 233: | ||
<math>f'''(t_{W_{2}}) \approx -307 < 0 \Rightarrow LRW</math> | <math>f'''(t_{W_{2}}) \approx -307 < 0 \Rightarrow LRW</math> | ||
<math>f'''(t_{W_{3}})\approx -117 < 0 \Rightarrow | <math>f'''(t_{W_{3}})\approx -117 < 0 \Rightarrow LRW</math> | ||
<math>f'''(t_{W_{4}})\approx 117 > 0 \Rightarrow | <math>f'''(t_{W_{4}})\approx 117 > 0 \Rightarrow RLW</math> | ||
An Rechts-links-Wendepunkten wird die Beschleunigung minimal und an den Links-rechts Wendepunkten maximal. | An Rechts-links-Wendepunkten wird die Beschleunigung minimal und an den Links-rechts Wendepunkten maximal. | ||
| Rechenweg anzeigen |Rechenweg verbergen}} | | Rechenweg anzeigen |Rechenweg verbergen}} | ||
'''Lösung:''' Die Achterbahn bremst zu den Zeitpunkten <math> | '''Lösung:''' Die Achterbahn bremst zu den Zeitpunkten <math>-0{,}87</math> Sekunden und <math>2{,}29</math> Sekunden am stärksten ab. Die Achterbahn beschleunigt zu den Zeitpunkten <math>-2{,}29</math> Sekunden und <math>0{,}87</math> Sekunden am stärksten. | ||
| Lösung anzeigen |Lösung verbergen}} | | Lösung anzeigen |Lösung verbergen}} | ||