Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
< Digitale Werkzeuge in der Schule | Basiswissen Analysis | Eigenschaften von Funktionen und Funktionsuntersuchung
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Farben korrigiert) Markierung: Quelltext-Bearbeitung 2017 |
||
| (52 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Box | 1=Merke | 2= | {{Box | 1=Merke | 2= | ||
Das '''Monotonieverhalten''' einer Funktion beschreibt den Verlauf des Graphen einer Funktion. Die | Das '''Monotonieverhalten''' einer Funktion beschreibt den Verlauf des Graphen einer Funktion. | ||
Die Monotonie gibt an, ob eine Funktion fällt, steigt oder konstant ist. | |||
Sei <math> | Sei <math>h(x)</math> eine Funktion und <math>x_1<x_2</math> | ||
- Falls auf einem Intervall <math> | - Falls auf einem Intervall <math>h(x_1) < h(x_2)</math> gilt, so ist die Funktion '''streng monoton steigend | ||
''' | ''' | ||
- Falls auf einem Intervall <math> | - Falls auf einem Intervall <math>h(x_1) \leq \ h(x_2)</math> gilt, so ist die Funktion '''monoton steigend''' | ||
- Falls auf einem Intervall <math> | - Falls auf einem Intervall <math>h(x_1) > h(x_2)</math> gilt, so ist die Funktion '''streng monoton fallend''' | ||
- Falls auf einem Intervall <math>h(x_1) \geq \ h(x_2)</math> gilt, so ist die Funktion '''monoton fallend''' | |||
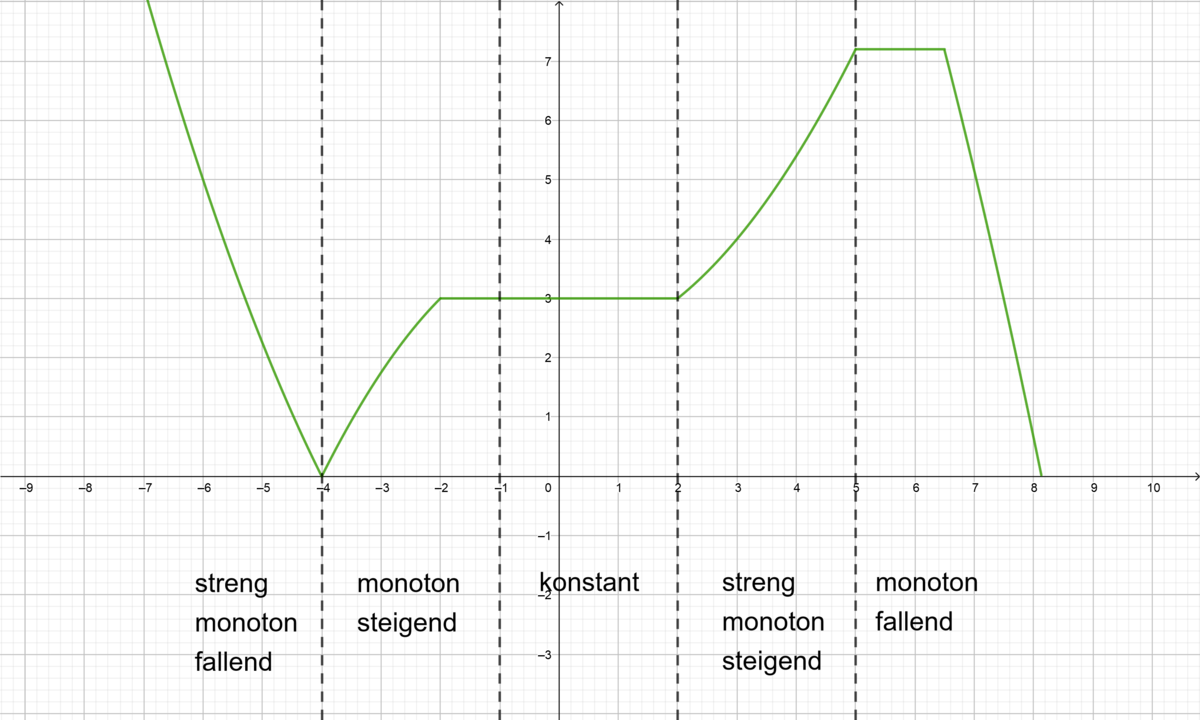
Wie die einzelnen Eigenschaften am Graphen aussehen, kannst du hier nochmal in der Abbildung sehen! | |||
[[Datei:MonotonieAbbildung.png|links|1200x1200px]] | [[Datei:MonotonieAbbildung.png|links|1200x1200px]] | ||
| Zeile 27: | Zeile 28: | ||
{{Box| 1= So berechnest du das Monotonieverhalten einer Funktion| 2= | {{Box| 1= Merke: So berechnest du das Monotonieverhalten einer Funktion| 2= | ||
1. Erste Ableitung berechnen | 1. Erste Ableitung berechnen | ||
| Zeile 37: | Zeile 38: | ||
4. Monotonietabelle aufstellen | 4. Monotonietabelle aufstellen | ||
5. Vorzeichen der Intervalle berechnen | 5. Vorzeichen der Intervalle berechnen (z.B. mit Taschenrechner) | ||
6. Ergebnis interpretieren | 6. Ergebnis interpretieren | ||
'''Beispiel: Monotonieverhalten für <math> | '''Beispiel: Monotonieverhalten für <math>f(x)=x^2</math> bestimmen ''' | ||
Zuerst berechnen wir die Ableitung <math> | Zuerst berechnen wir die Ableitung <math>f'(x)=2x</math>. Anschließend berechnen wir die Nullstellen der Ableitung (<math>f'(x)=0</math>) und erhalten durch Umformungen als Nullstelle <math>x=0</math>. | ||
Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math> | Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>]-\infty, 0[</math> und <math>]0,+\infty[</math>. Darauffolgend berechnen wir die Vorzeichen für die Intervalle. Dies machen wir indem wir Werte für die Ableitung in den entsprechenden Intervallen ausrechnen. Zum Beispiel liegt <math>-2</math> im Intervall <math>]-\infty, 0[</math> und <math> f'(-2)=-4 <0</math>. Die entsprechenden Werte kannst du in einer Tabelle übersichtlich darstellen: | ||
[[Datei:Monotonietabelle x^2.jpg| | [[Datei:Monotonietabelle f(x)=x^2.jpg|links|rahmenlos|900x900px]] | ||
(Legende: <math>\nearrow \widehat{=}</math> streng monoton steigend, <math>\searrow \widehat{=}</math> streng monoton fallend) | |||
Aus dem Ergebnis können wir schließen, dass die Funktion für <math> | Aus dem Ergebnis können wir schließen, dass die Funktion für <math>]-\infty, 0[</math> streng monoton fallend und für <math>]0,+\infty[</math> streng monoton steigend ist. | ||
| 3= | | 3=Merksatz}} | ||
{{Box | Aufgabe 2: Regenschauer am Aasee | | {{Box | Aufgabe 2: Regenschauer am Aasee | | ||
[[File:2004-09-07-Aasee Münster.jpg|thumb|Aasee Münster|alt=2004-09-07-Aasee Münster.jpg]] | [[File:2004-09-07-Aasee Münster.jpg|thumb|Aasee Münster|alt=2004-09-07-Aasee Münster.jpg]] | ||
Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion <math>g(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x</math> beschreibt die Zuflussgeschwindigkeit in den ersten 48 Stunden (<math>x=</math> Zeit in Stunden, <math>g(x)=</math> Zuflussgeschwindigkeit in Liter pro Stunde). Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab? | Nach einem starken Regenschauer in Münster steigt der Wasserspiegel im Aasee an. Die Funktion <math>g(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x</math> beschreibt die Zuflussgeschwindigkeit in den ersten 48 Stunden (<math>x\widehat{=}</math> Zeit in Stunden, <math>g(x)\widehat{=}</math> Zuflussgeschwindigkeit in Liter pro Stunde). Wann fließt innerhalb dieser Zeit Wasser zu und wann Wasser ab? | ||
{{Lösung versteckt|1=Stelle dir vor, wie sich der Graph verändert, wenn Wasser zu- bzw. abfließt |2=Tipp 1 |3=Schließen}} | |||
{{Lösung versteckt|1=Der Graph steigt monton, wenn Wasser dazufließt und fällt monoton, wenn Wasser abfließt. Also musst du die Monotonie der Funktion <math>g(x)</math> berechnen! |2=Tipp 2 |3=Schließen}} | |||
{{Lösung versteckt|1= Die Monotonie zeigt uns an, wo der Graph steigt und fällt. In dem Sachzusammenhang somit wann der Wasserspiegel zu und auch abnimmt. | {{Lösung versteckt|1= Die Monotonie zeigt uns an, wo der Graph steigt und fällt. In dem Sachzusammenhang somit wann der Wasserspiegel zu und auch abnimmt. | ||
| Zeile 65: | Zeile 69: | ||
<math>g(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x</math> | <math>g(x)=\frac{1}{4}x^{3} -\frac{25}{2}x^{2} +144x</math> | ||
<math>g'(x)=\frac{3}{4}x^{2} -25x + | <math>g'(x)=\frac{3}{4}x^{2} -25x +144</math> | ||
| Zeile 71: | Zeile 75: | ||
:Durch Umformungen erhalten wir die möglichen Extremstellen: | :Durch Umformungen erhalten wir die möglichen Extremstellen: | ||
:<math>\frac{3}{4}x^{2}-25x+ | :<math>\frac{3}{4}x^{2}-25x+144 =0\;\;\;\;\;\;\;\;|:\frac{3}{4}</math> | ||
:<math>\;x^{2}-\frac{100}{3}x+192 = 0\;\;\;\;\;\;\;\,|</math>PQ-Formel anwenden | :<math>\;x^{2}-\frac{100}{3}x+192 = 0\;\;\;\;\;\;\;\,|</math>PQ-Formel anwenden | ||
| Zeile 79: | Zeile 83: | ||
:<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= -\frac{-100}{3}\pm \sqrt{\Big(\frac{-100}{3}\Big)^{2}-\Big(192\Big)}</math> | :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= -\frac{-100}{3}\pm \sqrt{\Big(\frac{-100}{3}\Big)^{2}-\Big(192\Big)}</math> | ||
:<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 25,92</math> und <math> x_{2} = 7,40</math><br> | :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 25{,}92</math> und <math> x_{2} = 7{,}40</math><br> | ||
Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen: | Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen. Hierfür gehe wie im Beispiel vor: | ||
1. Stelle die Intervalle mithilfe deiner errechneten Nullstellen auf | |||
2. Berechne mithilfe deines Taschesrechners die Vorzeichen für die Intervalle | |||
{{Lösung versteckt|1=[[Datei:Tabelle für Aufgabe 2.jpg|links|rahmenlos|900x900px]] |2=Lösung für die Monotonietabelle |3=Schließen}} | |||
Antwort: Somit steigt der Wasserspiegel bis zur Stunde 7,4 (seit Messung). Danach fließt das Wasser ca. bis zur 26. Stunde ab. Anschließend steigt der Wasserspiegel wieder (beispielsweise durch einen erneuten Regenschauer) bis zum Ende des Messzeitraumes. | |||
Antwort: Somit | |||
|2=Lösung|3=Schließen}} | |2=Lösung|3=Schließen}} | ||
| Arbeitsmethode}} | |||
{{Box | Aufgabe 3: Der"SuperBounce"-Ball ⭐ | | {{Box | Aufgabe 3: Der"SuperBounce"-Ball ⭐ | | ||
[[File:Flummi gelb.jpg|thumb|SuperBounce-Ball]] | [[File:Flummi gelb.jpg|thumb|SuperBounce-Ball]] | ||
Die Firma "SuperBounce" hat einen speziellen Ball erfunden, der eine einzigartige Sprungbewegung beim Wurf auf dem Boden erzeugt | Die Firma "SuperBounce" hat einen speziellen Ball erfunden, der eine einzigartige Sprungbewegung beim Wurf auf dem Boden erzeugt. | ||
Die Funktion <math>f_a(x)=\frac{5}{6}x^{4}-a^{2}x^{2} (x \in [0, 4])</math> beschreibt annähernd die Flugbahn des Balles, wobei <math>a \in [-3, 3]</math> die Härte des Wurfes durch den Werfer beschreibt (<math>x\widehat{=}</math>Entfernung vom Abwurfort, <math>f_a(x)\widehat{=}</math>Höhe des Balles vom Abwurfort in cm). Bestimme wann der Ball in Abhängikeit von <math>a</math> nach oben springt und wann er fällt. | |||
{{Lösung versteckt|1=Überlege, wie sich das sprunghafte Verhalten des Balles im Graphen erkennen lässt. |2=Tipp |3=Schließen}} | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 105: | Zeile 112: | ||
Wir berechnen zuerst die Nullstellen der ersten Ableitung: | Wir berechnen zuerst die Nullstellen der ersten Ableitung: | ||
<math> | <math>f_a(x)=\frac{5}{6}x^{4}-a^{2}x^{2} </math> | ||
<math> | <math>f_a'(x)=\frac{20}{6}x^{3}-2a^{2}x</math> | ||
| Zeile 119: | Zeile 126: | ||
:<math>\Rightarrow x_{1} = 0</math> | :<math>\Rightarrow x_{1} = 0</math> | ||
:<math>\ | :<math>oder\;\;\;\;\;\;\ \frac{20}{6}x^{2} - 2a^{2} = 0\;\;\;\;\;\;\,\;|+2a^{2}</math> | ||
:<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \frac{20}{6}x^{2}= 2a^{2}\;\;\;\;|:\frac{20}{6}</math> | :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \frac{20}{6}x^{2}= 2a^{2}\;\;\;\;|:\frac{20}{6}</math> | ||
| Zeile 127: | Zeile 134: | ||
.<math> \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 0, x_{2} = \frac{\sqrt{15}}{5}a, </math> und <math> x_{3} =-\frac{\sqrt{15}}{5}a </math> | .<math> \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = 0, x_{2} = \frac{\sqrt{15}}{5}a, </math> und <math> x_{3} =-\frac{\sqrt{15}}{5}a </math> | ||
Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen: | Mithilfe der errechneten Intervalle können wir nun die Monotonietabelle aufstellen. Hierfür gehe wie im Beispiel vor: | ||
[ | 1. Stelle die Intervalle mithilfe deiner errechneten Nullstellen auf (Beachte: Wir betrachten die Funktion nur für Werte <math>(x \in [0, 4]</math>) | ||
2. Berechne mithilfe deines Taschesrechners die Vorzeichen für die Intervalle | |||
{{Lösung versteckt|1= [[Datei:Tabelle Aufgabe 3.jpg|links|rahmenlos|900x900px]] |2=Lösung für die Monotonietabelle |3=Schließen}} | |||
Antwort: Nach Abwurf fällt der Ball zunächst bis er <math>\frac{\sqrt{15}}{5}a</math> cm weit ist. Danch springt wieder hoch bis zum Ende der beobachteten Strecke <math>(x=4)</math>. | |||
|2=Lösung|3=Schließen}} | |||
| Arbeitsmethode}} | |||
| Zeile 180: | Zeile 191: | ||
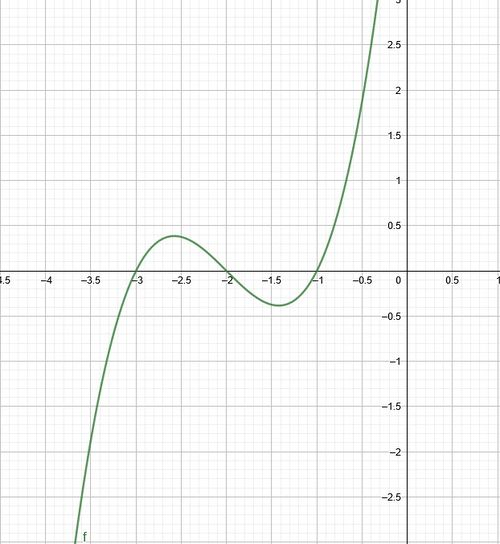
{{Lösung versteckt|1= Die Nullstellen von <math>h'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>. | {{Lösung versteckt|1= Die Nullstellen von <math>h'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>. | ||
Damit sind die zu betrachtenden Intervalle <math> | Damit sind die zu betrachtenden Intervalle <math>]-\infty, -3[</math>, <math>]-3, -2[</math>, <math>]-2, -1[</math> und <math>]-1, +\infty[</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math>h'(x)</math> an diesen <math><0</math> oder <math>>0</math> ist. | ||
Für <math> | Für <math>]-\infty, -3[</math> ist <math>h'(x)<0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math> | Für <math>]-3, -2[</math> ist <math>h'(x)>0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton steigend. | ||
Für <math> | Für <math>]-2, -1[</math> ist <math>h'(x)<0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton fallend. | ||
Für <math> | Für <math>]-1, +\infty[</math> ist <math>h'(x)>0</math>, somit ist <math>h(x)</math> auf diesem Intervall streng monoton steigend. |2=Lösung|3=Schließen}} | ||
| Zeile 219: | Zeile 230: | ||
Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen. |2=Lösung|3=Schließen}} | Farbe= | Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen. |2=Lösung|3=Schließen}} | Farbe={{Farbe|grün|dunkel}} | Arbeitsmethode}} | ||
{{Fortsetzung|weiter=Extrema|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Extrema|vorher=zurück|vorherlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung}} | {{Fortsetzung|weiter=Extrema|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Extrema|vorher=zurück|vorherlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung}} | ||