|
|
| (46 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) |
| Zeile 1: |
Zeile 1: |
| [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Testseite]]
| | {{Box|1=Info |2=In diesem Lernpfadkapitel kannst du dein Wissen über Funktionen und ihre Untersuchung anwenden, erweitern und dein Verständnis vertiefen. Um eine Funktion möglichst genau beschreiben zu können, gibt es verschiedene Eigenschaften, auf die hin man sie untersuchen kann. Zu diesen Eigenschaften gehören unter anderem Monotonie, Extrema, Wendepunkte und das Verhalten im Unendlichen und nahe Null. Unter den unten stehenden Links kannst du dir eine oder mehrere Eigenschaften aussuchen, über die du gerne mehr wissen oder deren Untersuchung du üben möchtest. |
| | |
| | |
| ===Allgemeine Hinweise===
| |
| | |
| {{Box|1=Lernpfad: Eigenschaften von Funktionen und Funktionsuntersuchung|2= | |
| Zuerst erklären wir Dir wichtige Begriffe und Zusammenhänge. Danach kannst Du selbständig die Aufgaben bearbeiten. Du benötigst Papier und Stifte, Lineal und Taschenrechner. Zu jedem Kapitel wurden Aufgaben beigefügt, die Dir dabei helfen das Wissen besser zu verstehen und zu vertiefen. Bei diesen Aufgaben handelt es sich um 3 verschiedene Schwierigkeitsstufen, die farblich gekennzeichnet sind:
| |
| :* '''<span style="color: orange">Schwierigkeitsstufe I mit gelbem Titel</span>''': leichte Aufgaben.
| |
| :* '''<span style="color: blue">Schwierigkeitsstufe II mit blauem Titel</span>''': mittelschwere Aufgaben.
| |
| :* '''<span style="color: green">Schwierigkeitsstufe III mit grünem Titel</span>''': schwere Aufgaben
| |
| | |
| Die mit einem Sternchen markierten Aufgaben sind insbesondere für den LK gedacht.
| |
| | |
| | |
| Viel Erfolg bei der Bearbeitung dieses Lernpfades!|3=Kurzinfo}}
| |
| | |
| ===Monotonie===
| |
| {{Box | 1=Merksatz | 2=
| |
| | |
| Das '''Monotonieverhalten''' einer Funktion
| |
| | |
| …beschreibt den Verlauf des Graphen einer Funktion. Die Montonie gibt an, ob eine Funktion fällt, steigt oder konstant ist.
| |
| | |
| | |
| Sei <math>f(x)</math> eine Funktion und <math>x_1<x_2</math>
| |
| | |
| - Falls auf einem Intervall <math>f(x_1) < f(x_2)</math> gilt, so ist die Funktion '''streng monoton steigend
| |
| '''
| |
| | |
| - Falls auf einem Intervall <math>f(x_1) \leq \ f(x_2)</math> gilt, so ist die Funktion '''monoton steigend'''
| |
| | |
|
| |
| | |
| - Falls auf einem Intervall <math>f(x_1) > f(x_2)</math> gilt, so ist die Funktion '''streng monoton fallend'''
| |
| | |
| - Falls auf einem Intervall <math>f(x_1) \geq \ f(x_2)</math> gilt, so ist die Funktion '''monoton fallend'''
| |
| | |
| | |
| | |
| [[Datei:MonotonieAbbildung.png|links|1200x1200px]]
| |
| | |
| | 3=Merke}}
| |
| | |
| {{Box | Aufgabe 1 |
| |
| {{LearningApp|width:100%|height:500px|app=p7pny09y220}} | Arbeitsmethode}}
| |
| | |
| | |
| {{Box| So berechnest du das Monotonieverhalten einer Funktion|
| |
| | |
| 1. Erste Ableitung berechnen
| |
| | |
| 2. Nullstellen der ersten Ableitung berechnen
| |
| | |
| 3. Intervalle benennen
| |
| | |
| 4. Monotonietabelle aufstellen
| |
| | |
| 5. Vorzeichen der Intervalle berechnen
| |
| | |
| 6. Ergebnis interpretieren
| |
| | Beispiel}}
| |
| | |
| {{Box| Beispiel: Monotonieverhalten für <math>g(x)=x^2</math> bestimmen |
| |
| Zuerst berechnen wir die Ableitung <math>g'(x)=2x</math>. Anschließend berechnen wir die Nullstellen der Ableitung (<math>g'(x)=0</math>) und erhalten durch Umformungen als Nullstelle <math>x=0</math>.
| |
| Damit sind die zu betrachtenden Intervalle für das Monotonieverhalten <math>(-\infty,0)</math> und <math>(0,+\infty)</math>. Darauffolgend stellen wir eine Monotonietabelle auf und berechnen die Vorzeichen für die Intervalle: | Beispiel}}
| |
| | |
| {| class="wikitable center"
| |
| |-
| |
| !
| |
| !<math> -\infty < x < 0 </math>
| |
| !<math> f'(0) </math>
| |
| !<math> 0 < x < \infty </math>
| |
| |-
| |
| |<math> f'(x) </math>
| |
| |<math> < 0 </math>
| |
| |<math> = 0 </math>
| |
| |<math> > 0</math>
| |
| |-
| |
| |<math> G_{f} </math>
| |
| |<math> \searrow </math>
| |
| |'''Tiefpunkt'''
| |
| |<math> \nearrow </math>
| |
| |}
| |
| | |
| Aus dem Ergebnis können wir schließen, dass die Funktion für <math>(-\infty,0)</math> streng monoton fallend und für <math>(0,+\infty)</math> streng monoton steigend ist.
| |
| | |
| {{Box | Aufgabe 2 |
| |
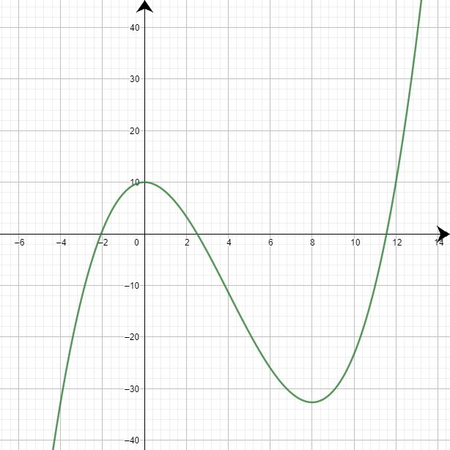
| a) Auf dem Bild siehst du den Graphen einer Ableitungsfunktion <math>f'(x)</math>. Welche Aussagen kannst du über das Monotonieverhalten von <math>f(x)</math> machen?
| |
| | |
| | |
| [[Datei:Graph der Funktion f'(x).jpg|links|alternativtext=|544x544px]]
| |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| {{Lösung versteckt|1=Erinnere dich daran, wie du bei der Berechnung des Monotonieverhaltens vorgehst. Welche Aussagen zum Monotonieverhalten liefert dir <math>f'(x)=0</math>? |2=Tipp 1|3=Schließen}}
| |
| | |
| {{Lösung versteckt|1=Die Nullstellen von <math>f'(x)</math> definieren die verschiedenen Intervalle, in denen das Monotonieverhalten von <math>f</math> verschieden ist. Nun kannst du betrachten, auf welchen Intervallen <math>f'(x)</math> <math><0</math> bzw. <math>>0</math> ist. Welche Aussagen kannst du damit über das Monotonieverhalten von <math>f(x)</math> machen? |2=Tipp 2|3=Schließen}}
| |
| | |
| {{Lösung versteckt|1= Die Nullstellen von <math>f'(x)</math> sind <math>x_1=-3, x_2=-2</math> und <math>x_3=-1</math>.
| |
| | |
| Damit sind die zu betrachtenden Intervalle <math>(-\infty, -3)</math>, <math>(-3, -2)</math>, <math>(-2, -1)</math> und <math>(-1, +\infty)</math>. Nun kannst du auf den verschiedenen Intervallen anhand des Graphen ablesen, ob <math>f'(x)</math> an diesen <math><0</math> oder <math>>0</math> ist.
| |
| | |
| Für <math>(-\infty, -3)</math> ist <math>f'(x)<0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton fallend.
| |
| | |
| Für <math>(-3, -2)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton steigend.
| |
| | |
| Für <math>(-2, -1)</math> ist <math>f'(x)<0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton fallend.
| |
| | |
| Für <math>(-1, +\infty)</math> ist <math>f'(x)>0</math>, somit ist <math>f(x)</math> auf diesem Intervall streng monoton steigend. |2=Lösung|3=Schließen}}
| |
| | |
| | |
| b) Zeichne nun mithilfe deiner Ergebnisse aus a) den Funktionsgraphen <math>f(x)</math> mithilfe deiner Kenntnisse über sein Monotonieverhalten in dein Heft.
| |
| | |
| {{Lösung versteckt|1=Dein Graph könnte in etwa so aussehen:
| |
| | |
| [[Datei:Graph f(x).jpg|links|544x544px]]
| |
|
| |
|
| | Zuerst erklären wir dir zu jeder Eigenschaft die wichtigen Begriffe und Zusammenhänge. Danach kannst du selbständig die Aufgaben bearbeiten. Dazu benötigst Papier und Stifte, Lineal und Taschenrechner. |
|
| |
|
| | Bei den Aufgaben unterscheiden wir folgende Typen: |
| | * In Aufgaben, die '''<span style="color: #F19E4F">orange</span>''' gefärbt sind, kannst du '''grundlegende Kompetenzen''' wiederholen und vertiefen. |
| | * Aufgaben in '''<span style="color: #5E43A5">blauer</span>''' Farbe sind '''Aufgaben mittlerer Schwierigkeit'''. |
| | * Und Aufgaben mit '''<span style="color: #89C64A">grünem</span>''' Streifen sind '''Knobelaufgaben'''. |
| | * Aufgaben, die mit einem ⭐ gekennzeichnet sind, sind nur für den LK gedacht. |
|
| |
|
| | Viel Erfolg! |
| | |3=Kurzinfo}} |
|
| |
|
| | ===Funktionsuntersuchung=== |
| | {{Box | Aufgabe: Funktionsuntersuchung |
| | |In der folgenden Aufgabe sollen die wichtigsten Begriffe zur Funktionsuntersuchung wiederholt werden. |
|
| |
|
| | Sieh dir den folgenden Graphen an und versuche in den darauffolgenden Lückentext die passenden Fachbegriffe einzufügen. Klicke auf die Lücken, um die Antwortmöglichkeiten zu erhalten. |
|
| |
|
| | [[Datei:Bild Lückentext.png|zentriert|mini|450x450px]] |
|
| |
|
| | {{LearningApp|width=100%|height=580px|app=pjemhayo320}}| Arbeitsmethode}} |
|
| |
|
|
| |
|
| | | ===Monotonie=== |
| | | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über Monotonie|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Monotonie}} |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| Möglich, weitere Lösungen für die Zeichnung des Graphen sind unter anderem Verschiebungen in Richtung der Ordinate, also nach unten und oben oder auch Streckungen bzw. Stauchungen. |2=Lösung|3=Schließen}} | Arbeitsmethode}}
| |
| | |
| | |
| | |
| | |
| | |
|
| |
|
| ===Extrema=== | | ===Extrema=== |
| | | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über Extrema|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Extrema}} |
| {{Box| Wissen | | |
| Im vorherigen Kapitel konntest du etwas über das Monotonie-Verhalten einer Funktion <math> f</math> erfahren. Dieses Wissen wird nun weiter vertieft und du lernst die sogenannten '''Extremstellen''' kennen, die in einem starken Zusammenhang mit dem Monotonie-Verhalten stehen.
| |
| | |
| Eine Funktion <math> f</math>, die in einem ersten Abschnitt streng monoton wächst und im darauf folgenden Abschnitt streng monoton fällt, muss einen Punkt besitzen an dem die Funktion weder steigt noch fällt und dieser Punkt wird als Maximum beziehungsweise Minimum bezeichnet.
| |
| | |
| Extrema werden bei einer Funktionsuntersuchung weitergehend darin unterschieden, ob es sich dabei um ein '''globales''' oder '''lokales''' Extremum handelt. Wichtig ist es dabei, dass du dein Intervall berücksichtigst.<br>
| |
| :* Es liegt ein '''lokales Extremum''' vor, wenn kein größerer oder kleinerer Funktionswert in einem betrachteten Intervall vorhanden ist.
| |
| :* Ein '''globales Extremum''' liegt vor, wenn kein größerer oder kleinerer Funktionswert des gesamten Graphen existiert.<br>
| |
| '''Merke:''' Die globalen Extremstellen sind besonders dann wichtig für dich, wenn du die Randwerte überprüfen sollst.
| |
| Die nachfolgende Übung soll Dir dabei den Unterschied verdeutlichen!
| |
| | |
| |Kurzinfo}}
| |
| | |
| {{Box | 1=<span style="color: orange">Aufgabe 1 - Extrema zuordnen</span>|2=
| |
| Ordne die Fachbegriffe den passenden Punkten der Funktion zu.
| |
| {{LearningApp|width:80%|height:450px|app=10658048}}
| |
| | 3=Arbeitsmethode}}
| |
| | |
| | |
| Nach dem du jetzt weißt was Extrema sind, sollst du erfahren, wie du diese schrittweise bestimmen kannst.
| |
| | |
| <br />{{Box| Extremstellenbestimmung |
| |
| Das Vorgehen setzt sich aus zwei Teilen zusammen, das für jede Funktion <math> f(x)</math> gilt:
| |
| | |
| :'''Notwendiges Kriterium:''' Für ein mögliches Extremum muss die Steigung 0 betragen. Im Folgenden wird diese als <math> x_E</math> bezeichnet. Es muss gelten: '''<math> f'(x_E) = 0</math>'''. <br>
| |
| | |
| :'''Hinreichendes Kriterium:''' Die potentiellen Extremstellen werden in <math> f''(x)</math> eingesetzt. Du musst darauf achten, dass dabei zwei Möglichkeiten entstehen. Für <math> f''(x_E)</math> kann folgen:
| |
| ::* <math>f''(x_E) < 0 \Rightarrow</math> Es liegt ein '''Hochpunkt''' vor.
| |
| ::* <math>f''(x_E) > 0 \Rightarrow</math> Es liegt ein '''Tiefpunkt''' vor.
| |
| :'''Ordinate bestimmen:''' Zu jeder Koordinate exisitert eine passende Ordinate. Dazu musst du <math>x_E</math> in <math>f(x)</math> einsetzen. Zusammenfassend erhälst du alle Extremstellen der Form <math>E(x_E/f(x_E))</math>.
| |
| | |
| '''Achtung:''' Im hinreichenden Kriterium besteht die Möglichkeit folgendes Ergebnis zu erhalten: '''<math>f''(x_E) = 0</math>'''. Dabei kann es sich um eine sogenannte '''Sattelstelle''' handeln. Diese Sattelstelle stellt einen besonderen Fall eines Extremums dar. Die zu erfüllenden Kriterien für eine Sattelstelle kannst du aus der unten abgebildeten Tabelle entnehmen.
| |
| | Merksatz}}
| |
| | |
| | |
| Die folgende Übersicht soll dir dabei helfen, die Kriterien der verschiedenen Extremstellen besser merken zu können:
| |
| {| class="wikitable center"
| |
| |-
| |
| !Art der Extremstelle
| |
| !Notwendiges Kriterium
| |
| !Hinreichendes Kriterium
| |
| |-
| |
| |Hochpunkt
| |
| |<math> f'(x_E) = 0</math>
| |
| |<math> f'(x_E) = 0</math> und <math> f''(x_E)</math> '''<''' <math>0</math>
| |
| |-
| |
| |Tiefpunkt
| |
| |<math> f'(x_E) = 0</math>
| |
| |<math> f''(x_E) = 0</math> und <math> f''(x_E)</math> '''>''' <math>0</math>
| |
| |-
| |
| |Sattelpunkt
| |
| |<math> f'(x_E) = 0</math> und <math> f''(x_E) = 0</math>
| |
| |<math> f'''(x_E) \neq 0</math>
| |
| |}
| |
| | |
| {{Box | Beispiel: Bestimmung von Extremstellen |
| |
| | |
| Wir untersuchen die folgende Funktion <math> f(x) = \frac{2}{3}x^{3} + 3x^{2} + 4x</math> auf Extremstellen.
| |
| # Zunächst bilden wir die erste Ableitung und setzen diese gleich null: <math> f'(x) = 2x^{2} + 6x + 4 = 0</math>. Umformungen dieser Gleichung liefern die möglichen Extremstellen <math> x_1 = -2</math> und <math> x_2 = -1</math>.
| |
| # Das bilden der zweiten Ableitung ergibt: <math> f''(x) = 4x + 6</math>
| |
| #* <math> f''(-2) = -2 < 0 \Rightarrow</math> Hochpunkt an der Stelle <math> x_1 = -2</math>.
| |
| #* <math> f''(-1) = +2 > 0 \Rightarrow</math> Tiefpunkt an der Stelle <math> x_2 = -1</math>.
| |
| # Es fehlen nun die Ordinaten, die wir durch das Einsetzen in <math> f(x)</math> bestimmen.
| |
| ::Wir erhalten: HP <math> \Big(-2/\frac{28}{3}\Big)</math> und TP <math> \Big(-1/-\frac{1}{3}\Big)</math>.
| |
| | Kurzinfo}}
| |
| | |
| | |
| In den beiden nachfolgenden Aufgaben kannst du dein Wissen nun überprüfen. In der 1. Aufgabe werden deine mathematischen Fähigkeiten unter Probe gestellt, um anschließend in Aufgabe 2 herausfinden zu können, ob du deine Ergebnisse auch im Sachzusammenhang interpretieren kannst.
| |
| | |
| <br />
| |
| | |
| {{Box |1= <span style="color: blue">Aufgabe 2 - Extrema bestimmen</span>|2=
| |
| | |
| Berechne die Extremstellen der folgenden Aufgabe. Jede Funktion besitzt einen unterschiedlich hohen Schwierigkeitsgrad. Wenn du dir noch nicht so sicher bist bei der Bestimmunng von Extremstellen, so solltest du die erste Aufgabe erarbeiten. Fühlst du dich jedoch gut vorbereitet und bist der Meinung du kannst auch komplexere Funktionen auf Extremstellen untersuchen. Dann versuche dein Können an der dritten Aufgabe.
| |
| | |
| : a) <math> f(x) = 2x^{2} - 6x + 4</math>
| |
| | |
| {{Lösung versteckt|1= Die Extrema werden durch das oben beschriebe Verfahren in drei Schritten bestimmt:<br>
| |
| ;Notwendiges Kriterium: <math> f'(x) = 0</math>, mit <math> f'(x) = 4x - 6</math>.
| |
| :Durch Umformungen erhalten wir die möglichen Extremstellen:
| |
| :<math>4x-6=0\;\;\;\;\;\;\;\;|-6</math>
| |
| :<math>\;\;\;\;\;\;4x=6\;\;\;\;\;|:4</math>
| |
| :<math>\;\;\;\;\;\;\;x=\frac{2}{3}</math><br>
| |
| ;Hinreichendes Kriterium: <math> f''(x_E) < 0</math> oder <math> f''(x_E) > 0</math>, mit <math> f''(x) = 4</math>.
| |
| :Wir erhalten durch einsetzen: <math>f''\Big(\frac{2}{3}\Big) = 4 > 0 \Rightarrow</math> Es handelt sich um einen Tiefpunkt bei <math>x = \frac{2}{3}.</math>
| |
| ;Ordinate bestimmen: <br>
| |
| :Wir setzen unsere Extremstelle in die Ursprungsfunktion ein: <math>f\Big(\frac{2}{3}\Big) = \frac{8}{9} \Rightarrow</math> '''TP''' <math>\Big(\frac{2}{3}/\frac{8}{9}\Big)</math>
| |
| |2= Lösung anzeigen |3=Lösung verbergen}}
| |
| | |
| : b) <math> g(x) = x^{3} - 3x^{2} - 5x + 6 </math>
| |
| | |
| {{Lösung versteckt|1= Die Extrema werden durch das oben beschriebe Verfahren in drei Schritten bestimmt:<br>
| |
| ;Notwendiges Kriterium: <math> f'(x) = 0</math>, mit <math> f'(x) = 3x^{2} - 6x - 5</math>.
| |
| :Durch Umformungen erhalten wir die möglichen Extremstellen:
| |
| :<math>3x^{2}-6x-5=0\;\;\;\;\;\;\;\;|:3</math>
| |
| :<math>\;x^{2}-2x-\frac{5}{3} = 0\;\;\;\;\;\;\;\,|</math>PQ-Formel anwenden
| |
| :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;x_{1/2} = -\frac{p}{2}\pm \sqrt{\Big(\frac{p}{2}\Big)^{2}-q}</math>
| |
| :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= -\frac{-2}{2}\pm \sqrt{\Big(\frac{-2}{2}\Big)^{2}-\Big(-\frac{5}{3}\Big)}</math>
| |
| :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;= 1 \pm \frac{163}{100}</math><br>
| |
| :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_1 = -\frac{63}{100}</math> und <math> x_2 = \frac{263}{100}</math><br>
| |
| ;Hinreichendes Kriterium: <math> f''(x_E) < 0</math> oder <math> f''(x_E) > 0</math>, mit <math> f''(x) = 6x - 6</math>.
| |
| :Wir erhalten durch einsetzen:
| |
| :<math>f''\Big(-\frac{63}{100}\Big) = -\frac{489}{50} < 0 \Rightarrow</math> Es handelt sich um einen Hochpunkt bei <math>x = -\frac{63}{100}.</math>
| |
| :<math>f''\Big(\frac{263}{100}\Big) = -\frac{489}{50} > 0 \Rightarrow</math> Es handelt sich um einen Tiefpunkt bei <math>x = \frac{263}{100}.</math>
| |
| ;Ordinate bestimmen: <br>
| |
| :Wir setzen unsere Extremstelle in die Ursprungsfunktion ein:
| |
| :<math>f\Big(-\frac{63}{100}\Big) = \frac{771}{100} \Rightarrow</math> '''HP''' <math>\Big(-\frac{63}{100}/\frac{771}{100}\Big)</math>
| |
| :<math>f\Big(\frac{263}{100}\Big) = -\frac{971}{100} \Rightarrow</math> '''TP''' <math>\Big(\frac{263}{100}/\frac{971}{100}\Big)</math>
| |
| |2= Lösung anzeigen |3=Lösung verbergen}}
| |
| | |
| : c) <math> h_{a}(x) = 5x^{5} -3a^{2}x^{3} </math> mit <math> a \in [1,5]</math>
| |
| | |
| <center><ggb_applet id="cset8amu" width="450" height="450" /></center>
| |
| | |
| {{Lösung versteckt|1= Die Extrema werden durch das oben beschriebe Verfahren in drei Schritten bestimmt:<br>
| |
| ;Notwendiges Kriterium: <math> h_{a}'(x) = 0</math>, mit <math> h_{a}'(x) = 25x^{4} - 9a^{2}x^{2}</math>.
| |
| :Durch Umformungen erhalten wir die möglichen Extremstellen:
| |
| :<math>\;\;\;\;\;\;25x^{4}-9a^{2}x^{2}=0\;\;\;\;\;\;\;|</math> Ausklammern
| |
| :<math>\;x^{2}\cdot(25x^{2}-9a^{2})=0\;\;\;\;\;\;\;|</math> Satz vom Nullprodukt
| |
| :<math>\Rightarrow x^{2} = 0 \Leftrightarrow x_{1/2} = 0</math>
| |
| :<math>\vee.\;\;\;\;\;\; 25x^{2} - 9a^{2} = 0\;\;\;\;\;\;\,\;|+9a</math>
| |
| :<math>\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; 25x^{2} = 9a^{2}\;\;\;\;|:25</math>
| |
| :<math>\;\;\;\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;x^{2} = \frac{9}{25}a^{2}\;|\sqrt{(...)}</math>
| |
| .<math> \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\Rightarrow x_{1} = -\frac{3}{5}a, x_{2} = 0</math> und <math> x_{4} = \frac{3}{5}a</math>
| |
| ;Hinreichendes Kriterium: <math> h_{a}''(x_E) < 0</math> oder <math> h_{a}''(x_E) > 0</math>, mit <math> h_{a}''(x) = 100x^{3} - 18a^{2}x</math>.
| |
| :Wir erhalten durch einsetzen:
| |
| :<math>h_{a}''\Big(-\frac{3}{5}a\Big) = -540a^{3} + 10,8a < 0 \Rightarrow</math> Es handelt sich um einen Hochpunkt bei <math>x = -\frac{3}{5}a.</math><br>
| |
| :<math>h_{a}''(0) = 0 \Rightarrow</math> Es handelt sich um einen möglichen Sattelpunkt bei <math>x = 0.</math> Dies muss überprüft werden!<br>
| |
| :<math>h_{a}''\Big(\frac{3}{5}a\Big) = 540a^{3} - 10,8a > 0 \Rightarrow</math> Es handelt sich um einen Tiefpunkt bei <math>x = \frac{3}{5}.</math><br>
| |
| : '''Achtung:''' Ob es sich um eine Sattelstelle bei <math>x = 0</math> handelt, wird durch die dritte Ableitung überprüft, indem wir zeigen, dass <math>h_{a}'''(0) \neq 0</math> stimmt. Es gilt <math>h_{a}'''(x) = 300x^{2} - 18a^{2}</math><br>
| |
| :<math>h_{a}'''(0) = -18a^{2} \neq 0 \Rightarrow</math> Es liegt ein Sattelpunkt vor.
| |
| ;Ordinate bestimmen: <br>
| |
| :Wir setzen unsere Extremstelle in die Ursprungsfunktion ein:
| |
| :<math>h_{a}\Big(-\frac{3}{5}a\Big) = \frac{162}{625}a \Rightarrow</math> '''HP''' <math>\Big(-\frac{3}{5}/\frac{162}{625}a\Big)</math>
| |
| :<math>h_{a}(0) = \frac{8}{9} \Rightarrow</math> '''SP''' <math>(0/0)</math>
| |
| :<math>h_{a}\Big(\frac{3}{5}a\Big) = -\frac{162}{625} \Rightarrow</math> '''TP''' <math>\Big(\frac{3}{5}/-\frac{162}{625}a\Big)</math>
| |
| |2= Lösung anzeigen|3=Lösung verbergen}}
| |
| | |
| | 3=Arbeitsmethode}}
| |
| | |
| {{Box |1= <span style="color: green">Aufgabe 3 - Anwendungsaufgabe</span>| 2=
| |
| Die Anzahl der Kunden eines Shopping-Centers wird für <math>9 \leq x \leq 20</math> mit Hilfe der Funktion <math>f(x) = -\frac{1}{2}x^{3} + \frac{19}{2}x^{2} + 55x - 900 </math> modelliert. Die Variable <math>x</math> stellt dabei die Zeit in Stunden dar.
| |
| :a) Bestimme die Uhrzeit, an der die Anzahl der Kunden am größten ist. Wie viele Besucher halten sich zu dieser Zeit im Shopping-Center auf?
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| ;'''Ableitungen bestimmen:'''
| |
| :<math> f'(x)=-\frac{3}{2}x^{2}+19x+55, f''(x)=-3x^{2}+19</math>
| |
| | |
| ;'''Notwendiges Kriterium:'''
| |
| ::<math> f'(x) = 0 \Leftrightarrow \Big(x_{1} = -\frac{243}{10}\Big) \vee. x_{2}=\frac{151}{10}</math>. Hier ist nur der zweite Wert von Relevanz, da der erste außerhalb des Definitionsbereiches liegt.
| |
| | |
| ;'''Hinreichendes Kriterium:'''
| |
| :<math> f''(x_{2}) = f''\Big(\frac{151}{10}\Big) = -\frac{263}{10} < 0 \Rightarrow</math> Es liegt ein Hochpunkt vor.
| |
| | |
| ;'''Ordinate bestimmen:'''
| |
| :<math> f\Big(\frac{151}{10}\Big) = 375,12. \;\;\;\;\;</math> '''Dieser Wert wird aufgerundet!'''
| |
| | |
| ;'''Antwortsatz:'''
| |
| :Um 15:07 Uhr besuchen die meisten Kunden das Shopping Center. Insgesamt sind es 376 Personen.
| |
| | |
| |2= Lösung anzeigen|3=Lösung verbergen}}
| |
| | |
| :b) Berechne <math> f'(12)</math> und beschreibe was dieser Wert im Sachzusammenhang bedeutet.
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| <math>f'(12)=67.</math> <br>
| |
| Die Ableitungsfunktion beschreibt die Anzahl der Kunden, die zu der Uhrzeit <math>x</math> das Shopping-Center betreten oder verlassen. Der Wert 67 bedeutet im Sachzusammenhang, dass um 12 Uhr 67 neue Kunden das Shopping-Center betreten.
| |
| | |
| |2= Lösung anzeigen |3=Lösung verbergen}}
| |
| | |
| :c) Um 10 Uhr betritt eine bestimmte Anzahl an Kunden das Shopping-Center. Berechne den Zeitpunkt an dem genauso viele Kunden das Center verlassen, wie sie es um 10 Uhr betreten haben.
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| Überlege Dir, wie die Zunahme und Abnahme von Kunden mathematisch betrachtet werden kann. Erinnere dich daran, dass man von einer positiven Zunahme spricht.
| |
| | |
| |2= Tipp anzeigen|3=Tipp verbergen}}
| |
| | |
| {{Lösung versteckt|1=
| |
| | |
| '''Bestimme die Anzahl neuer Kunden um 10 Uhr:'''
| |
| :<math> f'(10) = 95</math>
| |
| | |
| Hier muss ein Vorzeichenwechsel stattfinden, denn die Zunahme von Kunden bedeutet im mathematischen Sinne eine positive Zunahme. Da nach einer Uhrzeit gesucht, bei der Kunden das Shopping-Center verlassen, muss aus +95 -95 werden.
| |
| | |
| '''Bestimme die Uhrzeit zu der 95 Kunden das Shopping-Center verlassen:'''
| |
| :<math> f'(x) = -95 \Leftrightarrow x_{1/2} = -\frac{38}{6} \pm \sqrt{\Big(-\frac{38}{6}\Big)^{2} + 100}\Leftrightarrow \Big(x_{1} = -\frac{55}{10}\Big) \vee. x_{2} = \Big(\frac{1817}{100}\Big)</math>
| |
| | |
| '''Antwortsatz:''' Um 18:10 verlassen 95 Kunden das Shopping-Center.
| |
| | |
| |2= Lösung anzeigen|3=Lösung verbergen}}
| |
| | |
| | 3=Arbeitsmethode}}
| |
|
| |
|
| ===Wendepunkte=== | | ===Wendepunkte=== |
| | | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über Wendepunkte|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Wendepunkte}} |
| | |
| {{Box | Merke: Definition | | |
| '''Ein Wendepunkt''' beschreibt einen Punkt auf einem Funktionsgraphen an dem sich das '''Krümmungsverhalten des Graphes ändert'''. Der Funktionsgraph ändert an dieser Stelle seine Krümmung von rechts nach links (Rechts-links-Wendestelle, kurz: RLW) oder von links nach rechts (Links-rechts-Wendestelle, kurz: LRW).
| |
| | |
| Tipp: Es kann helfen, wenn man sich vorstellt auf dem Graphen mit einem Fahrrad zu fahren, so ist der Wendepunkt genau an dem Punkt, wo sich die Richtung, in die man lenkt, ändert.
| |
| | |
| | Merksatz}}
| |
| {{Box |1=<span style="color: orange">Aufgabe 1 - Wendepunkte angeben</span>
| |
| |2=Gib die Wendepunkte im Graphen an.
| |
| {{LearningApp|width:80%|height:450px|app=pasf50isa20}}|3=Arbeitsmethode}}
| |
| | |
| {{Box | Merke: Definition 2
| |
| |An einem '''Wendepunkt''' <math> x_W </math> einer Funktion <math>f(x)</math> ist die '''Steigung''' in der näheren Umgebung '''maximal bzw. minimal'''. Somit folgt, dass die Ableitung an dieser Stelle ein lokales Extremum aufweist. Daraus ergibt sich das notwendige Kriterium für einen Wendepunkt. Aus dem vorherigen Kapitel haben wir gelernt: Wenn die Funktion <math>f'(x)</math> im Punkt <math> x_W </math> einen Extrempunkt aufweist, so ist die Ableitung dieser Funktion <math>f''(x)</math> in diesem Punkt gleich 0. Das hinreichende Kriterium ergibt sich, wie im vorherigen Kapitel.
| |
| | |
| '''Zusammenfassung:'''
| |
| * '''notwendiges Kriterium:''' <math>f''(x_W)=0</math>
| |
| * '''hinreichendes Kriterium:''' <math>f'''(x_W) \neq 0</math>, '''Wobei gilt:''' <math>f'''(x_W) > 0 \Rightarrow</math>RLW oder <math>f'''(x_W) < 0 \Rightarrow</math>LRW
| |
| | Merksatz}}
| |
| {{Box| Berechnen des Wendepunktes|
| |
| * '''Notwendiges Kriterium:''' Nullstellen <math> x_W </math> der zweiten Ableitung berechnen
| |
| | |
| * '''Hinreichendes Kriterium:''' Einsetzen der berechneten Funktionstherms <math> x_W </math> in die dritte Ableitung (RLW oder LRW?)
| |
| | |
| * Berechnen des Funktionswertes durch einsetzen des Funktionstherms <math> x_W </math> in die Ursprüngliche Funktion
| |
| | |
| '''Beispiel:''' Gegeben sei die Funktion <math>f(x)=\frac{7}{12}x^4-5x^2</math>
| |
| * Notwendiges Kriterium: <math>f''(x_W)=0</math>
| |
| <math>f'(x)=\frac{28}{12}x^3-10x</math>
| |
| | |
| <math>f''(x)=\frac{84}{12}x^2-10=7x^2-10</math>
| |
| | |
| <math>f'''(x)=14x</math>
| |
| | |
| <math>f''(x_W)=7x_W^2-10=0 </math>
| |
| | |
| <math>\Rightarrow x_W^2=\frac{10}{7} </math>
| |
| | |
| <math>\Rightarrow x_W=\pm\sqrt{\frac{10}{7}}</math>
| |
| | |
| <math>\Rightarrow x_{W1}=+\sqrt{\frac{10}{7}}</math> und <math> x_{W2}=-\sqrt{\frac{10}{7}}</math>
| |
| | |
| * Hinreichendes Kriterium: <math>f'''(x_W)\neq 0</math>
| |
| <math>f'''(x_{W1})=20>0</math> und <math>f'''(x_{W2})=-20<0</math>
| |
| | |
| <math>\Rightarrow</math>An <math>x_{W1}</math> liegt eine Recht-links-Wendestelle und <math>\Rightarrow</math> an <math> x_{W2}</math> eine Links-rechts-Wendestelle vor.
| |
| | |
| Und nun du...
| |
| | |
| | Beispiel}}
| |
| {{Box|1= <span style="color: blue"> Aufgabe 2 - Wendepunkt bestimmen</span>
| |
| |2=Berechne die Wendepunkte der folgenden Funktion
| |
| | |
| <math> g(x) = \frac{2x^5}{25}-x^3+\frac{25x}{8} </math>
| |
| | |
| {{Lösung versteckt|'''Rechnung:''' Notwendiges Kriterium: <math>g''(x_W)=0</math>
| |
| | |
| <math>g'(x)=\frac{10x^4}{25}-3x^2+\frac{25}{8}</math>
| |
| | |
| <math>g''(x)=\frac{40x^3}{25}-6x=\frac{8}{5}x^3-6x</math>
| |
| | |
| <math>g'''(x)=\frac{24}{5}x^2-6</math>
| |
| | |
| <math>g''(x_W)=\frac{8}{5}x_W^3-6x_W=0 </math>
| |
| | |
| <math>\Rightarrow x_W\cdot(\frac{8}{5}x_W^2-6)=0 </math>
| |
| | |
| <math>\Rightarrow x_{W1}=0 </math> und <math>(\frac{8}{5}x_{W2/3}^2-6)=0 </math>
| |
| | |
| <math>\Rightarrow x_{W2/3}=\pm\sqrt{\frac{30}{8}}</math>
| |
| | |
| <math>\Rightarrow x_{W2}=+\sqrt{\frac{30}{8}}</math> und <math> x_{W3}=-\sqrt{\frac{30}{8}}</math>
| |
| | |
| * Hinreichendes Kriterium: <math>f'''(x_W)\neq 0</math>
| |
| <math>f'''(x_{W1})=-6<0</math> und <math>f'''(x_{W2})=12>0</math> und <math>f'''(x_{3})=-24<0</math>
| |
| | |
| <math>\Rightarrow</math>An <math>x_{W1}</math> liegt eine Links-rechts-Wendestelle, an <math> x_{W2}</math> eine Rechts-links-Wendestelle und an <math> x_{W3}</math> eine Links-rechts-Wendestelle vor.
| |
| | Lösung anzeigen |Lösung verbergen}}
| |
| | |
| | |
| | |
| |3=Arbeitsmethode}}
| |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
| | |
|
| |
|
| ===Verhalten im Unendlichen und nahe Null=== | | ===Verhalten im Unendlichen und nahe Null=== |
| | | {{Fortsetzung|weiter=Hier geht's weiter zum Abschnitt über das Verhalten im Unendlichen und nahe Null|weiterlink=Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung/Verhalten im Unendlichen und nahe Null}} |
| {{Box| Merke | | |
| Das '''Verhalten einer Funktion <math>f</math> im Unendlichen''' beschreibt, wie sich der Funktionswert <math>f(x)</math> verhält, wenn <math>x</math> gegen <math>\pm\infty</math> geht, also für sehr große positive und negative Werte von <math>x</math>. Bei ganzrationalen Funktionen der Form <math>f(x)=a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0</math> kann man das Verhalten im Unendlichen untersuchen, indem man sich den Summanden des Funktionsterms mit dem größten Exponenten von <math>x</math> anschaut. Betrachte also <math>g(x)=a_n x^n</math>. Im Unendlichen verhalten sich <math>f</math> und <math>g</math> gleich, du musst also nur das Verhalten im Unendlichen von <math>g</math> untersuchen. Es gibt vier Fälle, die du dabei unterscheiden musst:
| |
| | Merksatz}}
| |
| | |
| {| class="wikitable center"
| |
| !<math>n</math> gerade
| |
| !<math>n</math> ungerade
| |
| |-
| |
| |<math>n</math> gerade und <math>a_n>0</math>:
| |
| | |
| <math>f</math> verläuft "von links oben nach rechts oben",
| |
| | |
| <math>f(x)\rightarrow \infty</math> für <math>x\rightarrow\pm\infty</math>
| |
| |<math>n</math> ungerade und <math>a_n>0</math>:
| |
| | |
| <math>f</math> verläuft "von links unten nach rechts oben",
| |
| | |
| <math>f(x)\rightarrow -\infty</math> für <math>x\rightarrow -\infty</math>,
| |
| <math>f(x)\rightarrow \infty</math> für <math>x\rightarrow\infty</math>
| |
| |-
| |
| |<math>n</math> gerade und <math>a_n<0</math>:
| |
| | |
| <math>f</math> verläuft "von links unten nach rechts unten",
| |
| | |
| <math>f(x)\rightarrow -\infty</math> für <math>x\rightarrow\pm\infty</math>
| |
| |<math>n</math> ungerade und <math>a_n<0</math>:
| |
| | |
| <math>f</math> verläuft "von links oben nach rechts unten",
| |
| | |
| <math>f(x)\rightarrow \infty</math> für <math>x\rightarrow -\infty</math>,
| |
| <math>f(x)\rightarrow -\infty</math> für <math>x\rightarrow\infty</math>
| |
| |}
| |
| | |
| {{Box| Merke |
| |
| Das '''Verhalten einer Funktion <math>f</math> nahe Null''' beschreibt, wie sich der Funktionswert <math>f(x)</math> verhält, wenn <math>x</math> gegen Null geht, also für sehr kleine Werte von <math>x</math>. Eine ganzrationale Funktion der Form <math>f(x)=a_n x^n+a_{n-1}x^{n-1}+\ldots+a_1 x+a_0</math> verhält sich nahe Null wie die Summe aus dem absoluten Glied <math>a_0</math> und dem Summanden mit der geringsten Potenz von x, die im Funktionsterm auftaucht.
| |
| | Merksatz}}
| |
| | |
| {{Box| Beispiel 1|
| |
| <math>f(x)=5x^2-3x+4</math> verhält sich im Unendlichen wie <math>g(x)=5x^2</math>. Für <math>x\rightarrow -\infty</math> geht <math>f(x)\rightarrow\infty</math> und für <math>x\rightarrow \infty</math> geht <math>f(x)\rightarrow\infty</math>, da <math>n=2</math> eine gerade Zahl ist und <math>a_n=5>0</math>. Nahe Null verhält sich <math>f</math> wie <math>h(x)=-3x+4</math>. Wenn man sich ein kleines Intervall um <math>x=0</math> anschaut, sieht der Graph von <math>f</math> dort lokal also aus wie eine Gerade mit der Steigung -3 und dem y-Achsenabschnitt 4. Der y-Achsenabschnitt von <math>f</math> ist daher auch 4.
| |
| | Beispiel}}
| |
| | |
| {{Box| Beispiel 2|
| |
| <math>f(x)=x^5+4x^2-7</math> verhält sich im Unendlichen wie <math>g(x)=x^5</math>. Für <math>x\rightarrow -\infty</math> geht <math>f(x)\rightarrow -\infty</math> und für <math>x\rightarrow \infty</math> geht <math>f(x)\rightarrow\infty</math>, da <math>n=5</math> eine ungerade Zahl ist und <math>a_n=1>0</math> . Nahe Null verhält sich <math>f</math> wie <math>h(x)=4x^2-7</math>, also wie eine um den Faktor 4 gestreckte, nach oben geöffnete Parabel mit dem Scheitelpunkt (und y-Achsenabschnitt) bei <math>(0,-7)</math>.
| |
| | Beispiel}}
| |
| | |
| {{Box | 1=<span style="color: orange">Aufgabe 1 - Quiz zum Verhalten im Unendlichen</span> |
| |
| 2=Öffne das Quiz im Vollbildmodus und wähle die jeweils richtigen Antworten aus. Es können eine oder mehrere Antworten richtig sein. Es kann helfen, dir Notizen zu machen.
| |
| {{LearningApp|width:80%|height:1000px|app=10633191}}
| |
| | 3=Arbeitsmethode}}
| |
| | |
| {{Box | 1=<span style="color: green">Aufgabe 2* - Beschreibe das Verhalten</span> |
| |
| 2=Beschreibe in deinem Heft das Verhalten der nachfolgenden Funktionen und Funktionenscharen im Unendlichen '''und''' nahe Null. Gehe dazu vor wie in den Merkboxen oben.
| |
| | |
| '''a)''' <math>f(x)=x^2-\frac{4}{3}x^2-3x+9</math>
| |
| {{Lösung versteckt|1=Beachte, dass du manchmal den Funktionsterm erst zusammenfassen musst.|2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=Zusammengefasst ist <math>f(x)=-\frac{1}{3}x^2-3x+9</math>. <math>f</math> verhält sich daher im Unendlichen wie <math>g(x)=-\frac{1}{3}x^2</math>. Da <math>n=2</math> eine gerade Zahl ist und <math>a_n=-\frac{1}{3}<0</math>, geht <math>f(x)\rightarrow-\infty</math> für <math>x\rightarrow \pm\infty</math>. Der Graph von <math>f</math> verläuft also von links unten nach rechts unten.
| |
| |2=Lösung: Verhalten im Unendlichen|3=Lösung verbergen}}
| |
| {{Lösung versteckt|1=<math>f</math> verhält sich nahe Null wie <math>h(x)=-3x+9</math>, also wie eine fallende Gerade mit Steigung <math>-3</math> und y-Achsenabschnitt <math>9</math>.
| |
| |2=Lösung: Verhalten nahe Null|3=Lösung verbergen}}
| |
| | |
| '''b)''' <math>f_a(x)=-7x^5+ax^3</math> mit <math>a>0</math>
| |
| {{Lösung versteckt|1=Gehe bei Funktionenscharen genau so vor wie bei normalen Funktionen.|2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich im Unendlichen wie <math>g(x)=-7x^5</math>. Da <math>n=5</math> eine ungerade Zahl ist und <math>a_n=-7<0</math>, geht <math>f(x)\rightarrow\infty</math> für <math>x\rightarrow -\infty</math> und <math>f(x)\rightarrow-\infty</math> für <math>x\rightarrow \infty</math>. Der Graph von <math>f</math> verläuft also von links oben nach rechts unten.
| |
| |2=Lösung: Verhalten im Unendlichen|3=Lösung verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich nahe Null wie <math>h_a(x)=ax^3</math>, also wie eine Funktion dritten Gerades, die von links unten nach rechts oben geht, da <math>a</math> positiv ist. Der y-Achsenabschnitt ist <math>0</math>, da das absolute Glied im Funktionsterm von <math>f</math> nicht auftaucht und daher Null ist.
| |
| |2=Lösung: Verhalten nahe Null|3=Lösung verbergen}}
| |
| | |
| '''c)''' <math>f_a(x)=-ax^3+2x^2-\frac{4}{7}</math> mit <math>a<0</math>
| |
| {{Lösung versteckt|1=Überlege dir zunächst, welches Vorzeichen <math>a_n</math> hat, wenn <math>a</math> negativ ist. |2=Tipp|3=Tipp verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich im Unendlichen wie <math>g_a(x)=-ax^3</math>. Da <math>n=3</math> eine ungerade Zahl ist und <math>a_n=-a>0</math>, da <math>a<0</math> ist, geht <math>f(x)\rightarrow-\infty</math> für <math>x\rightarrow -\infty</math> und <math>f(x)\rightarrow\infty</math> für <math>x\rightarrow \infty</math>. Der Graph von <math>f</math> verläuft also von links unten nach rechts oben.
| |
| |2=Lösung: Verhalten im Unendlichen|3=Lösung verbergen}}
| |
| {{Lösung versteckt|1=<math>f_a</math> verhält sich nahe Null wie <math>h(x)=2x^2-\frac{4}{7}</math>, also wie eine nach oben geöffnete Parabel mit y-Achsenabschnitt <math>-\frac{4}{7}</math>.
| |
| |2=Lösung: Verhalten nahe Null|3=Lösung verbergen}}
| |
| | 3=Arbeitsmethode}}
| |
| | |
| ===Krümmung===
| |
| | |
| '''Text folgt'''
| |
| | |
| | |
| ===Zusammenfassung===
| |
| | |
| | |
| {{Box | 1=<span style="color: orange">Lückentext</span>|2=
| |
| | |
| | 3=Arbeitsmethode}}
| |
| | |
| {{Box | 1=<span style="color: green">Vollständige Kurvendisskusion</span>|2=
| |
| | |
| | 3=Arbeitsmethode}}
| |