Herta-Lebenstein-Realschule/Dezimalbrüche selbständig erarbeiten/1) Dezimalbrüche in der Stellenwerttafel: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(81 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
===Dezimalbrüche in der Stellenwerttafel:===
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}}<br>
{{Box|Merke!|Schreibe ins Heft:|Merksatz
 
{{Navigation|
[[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/1) Dezimalbr%C3%BCche_in_der_Stellenwerttafel|1) Dezimalbrüche in der Stellenwerttafel]]
 
[[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/2)_Dezimalbr%C3%BCche_in_Br%C3%BCche_umwandeln|2) Dezimalbrüche in Brüche umwandeln]]
 
[[Herta-Lebenstein-Realschule/Dezimalbrüche_selbständig_erarbeiten/3)_Brüche_in_Dezimalbrüche_umwandeln|3) Brüche in Dezimalbrüche umwandeln]]
 
[[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/4)_Periodische_Dezimalbr%C3%BCche|4) Periodische Dezimalbrüche]]
 
[[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/5)_Dezimalbr%C3%BCche_am_Zahlenstrahl_eintragen|5) Dezimalbrüche am Zahlenstrahl eintragen]]
 
[[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/6)_Vergleichen_und_Ordnen_von_Dezimalbr%C3%BCchen|6) Vergleichen und Ordnen von Dezimalbrüchen]]
 
[[Herta-Lebenstein-Realschule/Dezimalbr%C3%BCche_selbst%C3%A4ndig_erarbeiten/7)_Runden_von_Dezimalbr%C3%BCchen|7) Runden von Dezimalbrüchen]]
}}
}}
==1 Dezimalbrüche in der Stellenwerttafel==
Bearbeite die nachfolgende Applet des FLINK-Teams:
<ggb_applet id="xpytmrwu" width="810" height="580" border="888888" />
Originallink: https://www.geogebra.org/m/bjx9zkv5#material/zgutptw6


Dezimalbrüche sind Brüche in einer anderen Schreibweise: Sie haben den Nenner 10, 100, 1000, …
<ggb_applet id="zpv3vcvp" width="710" height="450" border="888888" />
Originallink: https://www.geogebra.org/m/bjx9zkv5#material/gy3ke58k


0,7 = <math>{7 \over 10}</math> ; die erste Stelle nach dem Komma sind die Zehntel<span style="Color:red"> '''z''' </span>(dezi).
 
{{Box|1=Merke|2=Schreibe ins Heft:<br>
0,08 = <math>{8 \over 100}</math> ; die zweite Stelle nach dem Komma sind die Hundertstel<span style="Color:red"> '''h''' </span>(centi).
Dezimalbrüche sind Brüche in einer anderen Schreibweise: Sie haben den Nenner 10, 100, 1000, …<br>
0,7 = <math>{7 \over 10}</math> ; die erste Stelle nach dem Komma sind die Zehntel<span style="Color:red"> '''z''' </span>(dezi).<br>
0,004 = <math>{4 \over 1000}</math> ; die dritte Stelle sind Tausendstel<span style="Color:red"> '''t''' </span>(milli).
0,08 = <math>{8 \over 100}</math> ; die zweite Stelle nach dem Komma sind die Hundertstel<span style="Color:orange"> '''h''' </span>(centi).<br>
0,004 = <math>{4 \over 1000}</math> ; die dritte Stelle sind Tausendstel<span style="Color:green"> '''t''' </span>(milli).<br>
Die Ziffern hinter dem Komma heißen '''Nachkommaziffern''' oder '''Dezimalen'''.
Die Ziffern hinter dem Komma heißen '''Nachkommaziffern''' oder '''Dezimalen'''.<br>
Dezimalbrüche lassen sich in einer '''Stellenwerttafel''' darstellen:
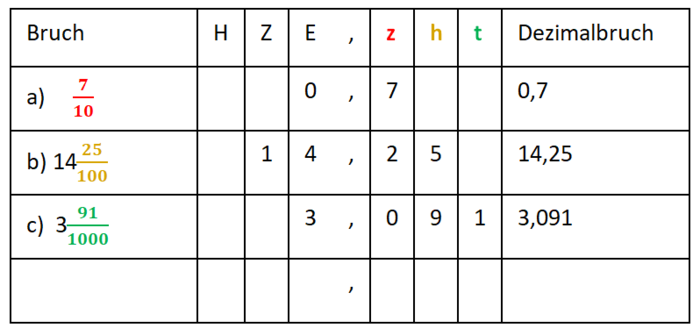
Dezimalbrüche lassen sich in einer '''Stellenwerttafel''' darstellen:
[[Datei:Stellenwerttafel.png|links|mini|700x700px]]
[[Datei:Stellenwerttafel.png|700px|center]]
 
|3=Merksatz}}
 
<br>
Dezimalzahlen lassen sich auch am Zahlenstrahl darstellen:
{{Box|Zahlenstrahl-Lupe|Du kannst zwischen den natürlichen Zahlen auf dem Zahlenstrahl weitere Zahlen eintragen. Schau mit der Lupe!|Unterrichtsidee}}
<ggb_applet id="rajsk9m7" width="961" height="395" border="888888" />
Originallink: https://www.geogebra.org/m/ykgs7ydx  <br>
Applet von B. Lachner<br>


{{Box|Dezimalzahlen darstellen|Im nachfolgenden Applet kannst du die Dezimalzahlen als Bruchteile darstellen. Erkläre!|Unterrichtsidee}}
<ggb_applet id="a3pehc4h" width="1100" height="757" border="888888" />
Originallink: https://www.geogebra.org/m/vsmtnrq3<br>
Applet von B. Lachner
<br>
{{Box|Übung 1|Bearbeite die folgenden Apps.|Üben}}
{{LearningApp|app=pi813ph2c22|width=100%|height=600px}}


{{LearningApp|app=pgufv76xj22|width=100%|height=400px}}


{{h5p-zum|id=19991|height=600}}


{{h5p-zum|id=20181|height=600}}


{{LearningApp|app=ppzvvcetc20|width=100%|height=600px}}


{{LearningApp|app=pkvdywpga20|width=100%|height=600px|}}


{{LearningApp|app=pri52nu7t22|width=100%|height=800px}}


<ggb_applet id="vjmxabfu" width="630" height="540" border="888888" />
Applet des FLINK-Teams, Originallink: https://www.geogebra.org/m/bjx9zkv5#material/wm6mgpaw
<ggb_applet id="ek2cnr6m" width="650" height="500" border="888888" />
Applet des FLINK-Teams, Originallink: https://www.geogebra.org/m/bjx9zkv5#material/z8zvnprt
<ggb_applet id="wbd5hup5" width="780" height="580" border="888888" />
Applet des FLINK-Teams, Originallink: https://www.geogebra.org/m/bjx9zkv5#material/xfgnwee5


{{Box|Übung 2 im Heft|Löse die Aufgaben aus dem Buch. Löse im Heft.
* S. 105 Nr. 1
* S. 105 Nr. 2|Üben}}


{{Box|Übung 3 - online|Löse auf der Seite [https://aufgabenfuchs.de/mathematik/bruch/dezimalbruch.shtml Aufgabenfuchs] die Aufgaben
* 1
* 2
* 3
* 4 |Üben}}




{{Box|Überflüssige Nullen|
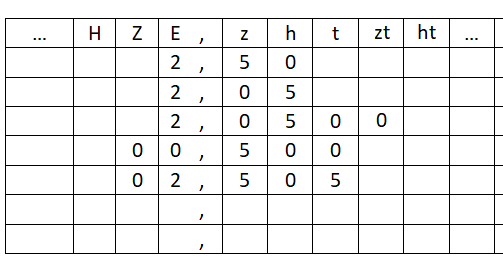
Zeichne eine Stellenwerttafel in dein Heft und trage die folgenden Dezimalbrüche ein:


a) 2,50  b) 2,05    c) 2,0500    d) 00,500   e) 02,505


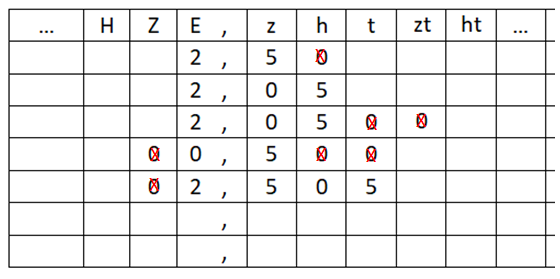
Welche Nullen kann man bei jeder Zahl weglassen, ohne dass sich der Wert des Dezimalbruches ändert?
Formuliere eine Regel.|Arbeitsmethode}}
{{Lösung versteckt|Schreibe die Zahlen in eine Stellenwerttafel:[[Datei:Unnötige Nullen Tipp Stellenwerttafel.png]]|Tipp 1: Stellenwerttafel|Verbergen}}
{{Lösung versteckt|Welche Nullen dürfen weggelassen werden, ohne dass sich der Wert der Zahl ändert?[[Datei:Unnötige Nullen Tipp 2 Stellenwerttafel.png]]|Tipp 2: Unnötige Nullen streichen|Verbergen}}
Das folgende Quiz soll dir helfen, eine Regel zu formulieren.
{{H5p-zum|id=20182|height=400}}


Vergleiche deine Regel mit dem Lückentext. Falls nötig, ergänze und berichtige deine Regel.
<br>
<br>


{{Box|Üben|Bearbeite die folgenden Apps.|Üben}}
{{Box| Übung 4|Schreibe die Zahlen ohne unnötige Nullen.|Üben}}
{{LearningApp|width:100%|high:1500px|app=ppzvvcetc20}}
{{LearningApp|app=pzj6m66f520|width=100%|height=400px}}


{{Box|1=Übung 5|2=Bearbeite die Aufgabe aus dem Buch. Löse im Heft.
* S. 105 Nr. 7
<br> '''Beachte den <u>Tipp zu Nr. 7</u>. <span style="color:green"> Genau so musst du alle Aufgaben bearbeiten!'''</span> <br>Schreibe immer zunächst die Aufgabe ab und schreibe dann - wenn möglich - nach Umwandlung in einen Bruch ohne die unnötigen Nullen (ähnlich wie in der App oben).|3=Üben}}


{{LearningApp|width:100%|high:1500px|app=pkvdywpga20}}
{{Lösung versteckt|1='''Notiere das folgende Beispiel''' für die Bearbeitung: Nr. 7a (erster Dezimalbruch)<br> Bearbeite die folgenden Aufgaben in derselben Weise.<br>[[Datei:S 105 - Nr 7a (Beispiel).jpg|400 px|center]]|2=Tipp zu Nr. 7|3=Tipp ausblenden}}
{{Lösung versteckt|1=<span style="color:grey">Bei dir müssen neben einem Antwortsatz (wie dem folgenden) zusätzlich '''alle 12 Umwandlungen zu den Teilaufgaben im Heft''' notiert werden!</span><br><u>Erkenntnis:</u><br> Ist bei einem Dezimalbruch die letzte Nachkommaziffer eine Null, so kann diese weggelassen werden, ohne dass sich der Wert ändert.|2=Lösung zu Nr. 7|3=Tipp ausblenden}}


{{LearningApp|width:100%|high:1500px|app=p6urs5k1t20}}


Weiter geht es mit
<br />


[[Buss-Haskert/Dezimalbrüche selbständig erarbeiten/2) Dezimalbrüche in Brüche umwandeln|2) Dezimalbrüche in Brüche umwandeln]]
{{Fortsetzung|weiter=2) Dezimalbrüche in Brüche umwandeln|weiterlink=Herta-Lebenstein-Realschule/Dezimalbrüche selbständig erarbeiten/2) Dezimalbrüche in Brüche umwandeln|vorher=zurück zur Startseite|vorherlink=Herta-Lebenstein-Realschule/Dezimalbrüche selbständig erarbeiten}}

Aktuelle Version vom 23. Dezember 2022, 08:15 Uhr

zurück zur Seite der Herta-Lebenstein-Realschule


1 Dezimalbrüche in der Stellenwerttafel

Bearbeite die nachfolgende Applet des FLINK-Teams:

GeoGebra

Originallink: https://www.geogebra.org/m/bjx9zkv5#material/zgutptw6

GeoGebra

Originallink: https://www.geogebra.org/m/bjx9zkv5#material/gy3ke58k


Merke

Schreibe ins Heft:
Dezimalbrüche sind Brüche in einer anderen Schreibweise: Sie haben den Nenner 10, 100, 1000, …
0,7 =  ; die erste Stelle nach dem Komma sind die Zehntel z (dezi).
0,08 =  ; die zweite Stelle nach dem Komma sind die Hundertstel h (centi).
0,004 =  ; die dritte Stelle sind Tausendstel t (milli).
Die Ziffern hinter dem Komma heißen Nachkommaziffern oder Dezimalen.
Dezimalbrüche lassen sich in einer Stellenwerttafel darstellen:

Stellenwerttafel.png


Dezimalzahlen lassen sich auch am Zahlenstrahl darstellen:

Zahlenstrahl-Lupe
Du kannst zwischen den natürlichen Zahlen auf dem Zahlenstrahl weitere Zahlen eintragen. Schau mit der Lupe!
GeoGebra

Originallink: https://www.geogebra.org/m/ykgs7ydx
Applet von B. Lachner


Dezimalzahlen darstellen
Im nachfolgenden Applet kannst du die Dezimalzahlen als Bruchteile darstellen. Erkläre!
GeoGebra

Originallink: https://www.geogebra.org/m/vsmtnrq3
Applet von B. Lachner

Übung 1
Bearbeite die folgenden Apps.








GeoGebra

Applet des FLINK-Teams, Originallink: https://www.geogebra.org/m/bjx9zkv5#material/wm6mgpaw

GeoGebra

Applet des FLINK-Teams, Originallink: https://www.geogebra.org/m/bjx9zkv5#material/z8zvnprt

GeoGebra

Applet des FLINK-Teams, Originallink: https://www.geogebra.org/m/bjx9zkv5#material/xfgnwee5


Übung 2 im Heft

Löse die Aufgaben aus dem Buch. Löse im Heft.

  • S. 105 Nr. 1
  • S. 105 Nr. 2


Übung 3 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

  • 1
  • 2
  • 3
  • 4


Überflüssige Nullen

Zeichne eine Stellenwerttafel in dein Heft und trage die folgenden Dezimalbrüche ein:

a) 2,50  b) 2,05    c) 2,0500    d) 00,500   e) 02,505

Welche Nullen kann man bei jeder Zahl weglassen, ohne dass sich der Wert des Dezimalbruches ändert?

Formuliere eine Regel.
Schreibe die Zahlen in eine Stellenwerttafel:Unnötige Nullen Tipp Stellenwerttafel.png
Welche Nullen dürfen weggelassen werden, ohne dass sich der Wert der Zahl ändert?Unnötige Nullen Tipp 2 Stellenwerttafel.png

Das folgende Quiz soll dir helfen, eine Regel zu formulieren.


Vergleiche deine Regel mit dem Lückentext. Falls nötig, ergänze und berichtige deine Regel.


Übung 4
Schreibe die Zahlen ohne unnötige Nullen.


Übung 5

Bearbeite die Aufgabe aus dem Buch. Löse im Heft.

  • S. 105 Nr. 7

Beachte den Tipp zu Nr. 7. Genau so musst du alle Aufgaben bearbeiten!
Schreibe immer zunächst die Aufgabe ab und schreibe dann - wenn möglich - nach Umwandlung in einen Bruch ohne die unnötigen Nullen (ähnlich wie in der App oben).
Notiere das folgende Beispiel für die Bearbeitung: Nr. 7a (erster Dezimalbruch)
Bearbeite die folgenden Aufgaben in derselben Weise.
S 105 - Nr 7a (Beispiel).jpg
Bei dir müssen neben einem Antwortsatz (wie dem folgenden) zusätzlich alle 12 Umwandlungen zu den Teilaufgaben im Heft notiert werden!
Erkenntnis:
Ist bei einem Dezimalbruch die letzte Nachkommaziffer eine Null, so kann diese weggelassen werden, ohne dass sich der Wert ändert.



zurück zur Startseite
2) Dezimalbrüche in Brüche umwandeln
Abgerufen von „https://projekte.zum.de/index.php?title=Herta-Lebenstein-Realschule/Dezimalbrüche_selbständig_erarbeiten/1)_Dezimalbrüche_in_der_Stellenwerttafel&oldid=72677“