Julius-Echter-Gymnasium/Mathematik/Flächeninhalt von Trapezen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Main>Franzi gls JEG Keine Bearbeitungszusammenfassung |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (16 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
< | {{Box|Trapez|Ein Viereck mit '''genau einem Paar''' zueinander parallelen Seiten nennt man ein '''Trapez'''.<br /> | ||
''' | Im Bild sind die Seiten a und c parallel zueinander. <br /> | ||
Wie du sehen kannst, müssen diese Seiten auch nicht gleich lang sein.<br /> | |||
Der Abstand zwischen den parallelen Seiten heißt '''Höhe'''. <br /> | |||
Die beiden anderen Seiten sind die sogenannten Schenkel (hier im Bild sind das die Seiten b und d).|Kurzinfo}} | |||
[[Datei:Trapez.png|300px|regelmäßiges Trapez]] | |||
<br /> | |||
{{Box|Flächeninhalt von Trapezen|Um den Flächeninhalt eines Trapezes zu berechnen, musst du die beiden parallelen Seiten addieren und diese Summe mit der zugehörigen Höhe multiplizieren. <br /> | |||
Dieses Produkt musst du dann noch halbieren. |Merksatz}} | |||
Die Formel lautet: <span style="Color: red">'''A = <math> \frac{1}{2}</math> · (a+c) · h'''</span> | |||
<span style="Color: green">Wichtig: Du darfst für diese Formel nur die beiden parallelen Seiten und '''deren gemeinsame Höhe''' verwenden!</span> | |||
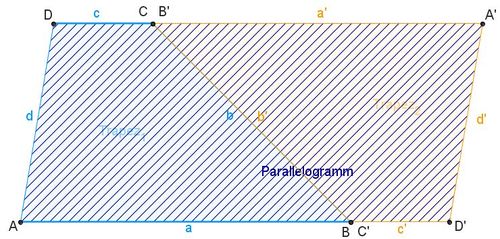
[[Datei:Zwei Trapeze ergeben ein Parallelogramm.jpg|500px|Zwei Trapeze ergeben ein Parallelogramm]] | |||
{{Box|Erläuterung der Formel:|Dreht man das Trapez um 180° und hängt es an die Seite des vorhandenen Trapezes, so entsteht ein Parallelogramm mit der Grundlinie '''a+c'''. <br /> | |||
Parallelogramm und Trapez haben die gleiche Höhe '''h'''.<br /> | |||
Da das Parallelogramm genau so groß ist wie die beiden Trapeze zusammen, kann man über die Flächeninhaltsformel des Parallelogramms die neue Flächeninhaltsformel für das Trapez ermitteln: <br /> | |||
Das ursprüngliche Trapez ist also '''genau halb so groß''' wie das Parallelogramm mit der Grundlinie a+c und der Höhe h.<br /> | |||
|Arbeitsmethode}} | |||
< | Hiermit entsteht also die Formel '''A = <math> \frac{1}{2}</math> · (a+c) · h ''' | ||
<br /> | |||
Teste nun dein Wissen über den Flächeninhalt von Trapezen: | |||
{{Box|Aufgabe 1|{{LearningApp|app=prxx1havc18|width=100%|height=500px}}|Üben}} | |||
Bei den nächsten Aufgaben kannst du nochmal verschiedene Flächeninhaltsformeln wiederholen: | |||
{{Box|Aufgabe 2|{{LearningApp|app=7586570|width=100%|height=500px}}|Üben}} | |||
{{Box|Aufgabe 3|{{LearningApp|app=p0kkitpqk20|width=100%|height=850px}}|Üben}} | |||
{{Box|Aufgabe 4|{{LearningApp|app=2329547|width=100%|height=500px}}|Üben}} | |||
<br /> | |||
{{Fortsetzung|weiter=Schrägbilder|weiterlink=Julius-Echter-Gymnasium/Mathematik/Schrägbilder|vorher=Flächeninhalt von Dreiecken|vorherlink=Julius-Echter-Gymnasium/Mathematik/Flächeninhalt_von_Dreiecken}} | |||
{{SORTIERUNG:{{SUBPAGENAME}}}} | |||
[[Kategorie:Julius-Echter-Gymnasium Mathematik]] | |||
Aktuelle Version vom 23. Februar 2020, 13:59 Uhr
Die Formel lautet: A = · (a+c) · h
Wichtig: Du darfst für diese Formel nur die beiden parallelen Seiten und deren gemeinsame Höhe verwenden!
Hiermit entsteht also die Formel A = · (a+c) · h
Teste nun dein Wissen über den Flächeninhalt von Trapezen:
Bei den nächsten Aufgaben kannst du nochmal verschiedene Flächeninhaltsformeln wiederholen: