Benutzer:Lena H. WWU-5/Quadratische Funktionen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (17 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
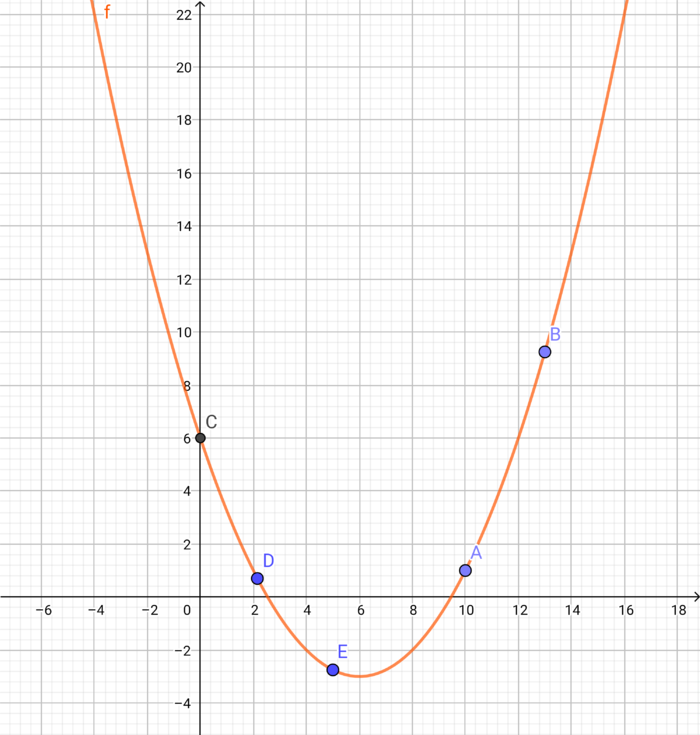
{{Box|Berechne Die x- bzw. die y-Koordinate der Punkte, sodass diese auf der Funktion f liegen.|Gegeben sei die Funktion <math>f(x) =\frac {1} {4} \cdot (x-6)^2-3</math> und die Punkte <math> A=(10|?), B=(? |\frac {29} {4}), C=(?|5), D=(\frac {43} {20}|?) </math> und <math>E=(5|?) </math> | {{Box|1= <span style="color: blue" >3. Berechne Die x- bzw. die y-Koordinate der Punkte, sodass diese auf der Funktion f liegen. </span>|2=Gegeben sei die Funktion <math>f(x) =\frac {1} {4} \cdot (x-6)^2-3</math> und die Punkte <math> A=(10|?), B=(? |\frac {29} {4}), C=(?|5), D=(\frac {43} {20}|?) </math> und <math>E=(5|?) </math> <br /> <br /> | ||
''' a) ''' Berechne von den oben genannten Punkten die jeweils fehlende x- bzw. y-Koordinate, so dass die Punkte auf der Funktion f liegen. <br /><br /> | ''' a) ''' Berechne von den oben genannten Punkten die jeweils fehlende x- bzw. y-Koordinate, so dass die Punkte auf der Funktion f liegen. <br /><br /> | ||
{{Lösung versteckt| 1= Was bedeuten die Variable <math> x </math> und <math> f(x) </math>? Wofür sind sie Platzhalter? | 2= Tipp 1| 3= schließen}} | {{Lösung versteckt| 1= Was bedeuten die Variable <math> x </math> und <math> f(x) </math>? Wofür sind sie Platzhalter? | 2= Tipp 1| 3= schließen}} | ||
{{Lösung versteckt| 1= Wenn du die x-Koordinate eines Punktes in eine Funktion einsetzt, berechnest du so seine y-Koordinate. | 2= Tipp 2| 3=schließen}} | {{Lösung versteckt| 1= Wenn du die x-Koordinate eines Punktes in eine Funktion einsetzt, berechnest du so seine y-Koordinate. | 2= Tipp 2| 3=schließen}} | ||
{{Lösung versteckt | 1= Die Punkte besitzen, um auf der Funktion <math> f(x) </math> zu liegen, folgende Koordinaten: <br /> | |||
<math>A=(10|1),, B=(13|\frac {29} {4}) , C=(0|5), D=(\frac{43} {20}|\frac{7}{10}) </math> und <math>E=(5|-\frac{11} {4}) </math>| 2=Lösung zu a) | 3= schließen}} | |||
''' b) ''' Zeichne den Graphen der Funktion f mit den oben genannten Punkte nun in dein Heft. <br /><br /> | ''' b) ''' Zeichne den Graphen der Funktion f mit den oben genannten Punkte nun in dein Heft. <br /><br /> | ||
{{Lösung versteckt| 1= Du weißt nicht, wie Du mit Deiner Zeichnung anfangen sollst? Dann schau doch noch einmal in den Lückentext von Aufgabe 1.| 2=Tipp 3 | 3=schließen}} | {{Lösung versteckt| 1= Du weißt nicht, wie Du mit Deiner Zeichnung anfangen sollst? Dann schau doch noch einmal in den Lückentext von Aufgabe 1.| 2=Tipp 1 | 3=schließen}} | ||
{{Lösung versteckt| 1= Welcher Punkt ist in einer Funktion der Form <math>g(x)=a\cdot(x-d)^2+e</math> als erstes ablesbar? Beginne deine Zeichnung mit diesem Punkt. | 2= Tipp 2| 3= schließen}} | |||
{{Lösung versteckt| 1= | {{Lösung versteckt| 1= In einer Funktionsgleichung der Form <math>g(x)=a\cdot(x-d)^2+e</math> gibt dir der Parameter <math> a</math>, wie viele Einheiten sich der Graph nach oben oder unten bewegen muss, wenn er sich um eine Einheit nach rechts bewegt.| 2=Tipp 3 | 3=schließen}} | ||
{{Lösung versteckt |1= Wenn deine Zeichnung wie folgt aussieht, hast du alles richtig gemacht: [[Datei: Lösung Aufgabe 3.png|700px | zentriert]] |2=Lösung b) |3=schließen | {{Lösung versteckt |1= Wenn deine Zeichnung wie folgt aussieht, hast du alles richtig gemacht: [[Datei: Lösung Aufgabe 3.png|700px | zentriert]] |2=Lösung zu b) |3=schließen | ||
}} | }} | ||
}} | }} | ||
{{Box|Berechnung von Nullstellen| | ===Nullstellen=== | ||
{{Box|1= <span style="color: blue"> 6. Berechnung von Nullstellen </span>|2= | |||
Gegeben seien folgende Funktionen: <br /> | Gegeben seien folgende Funktionen: <br /> | ||
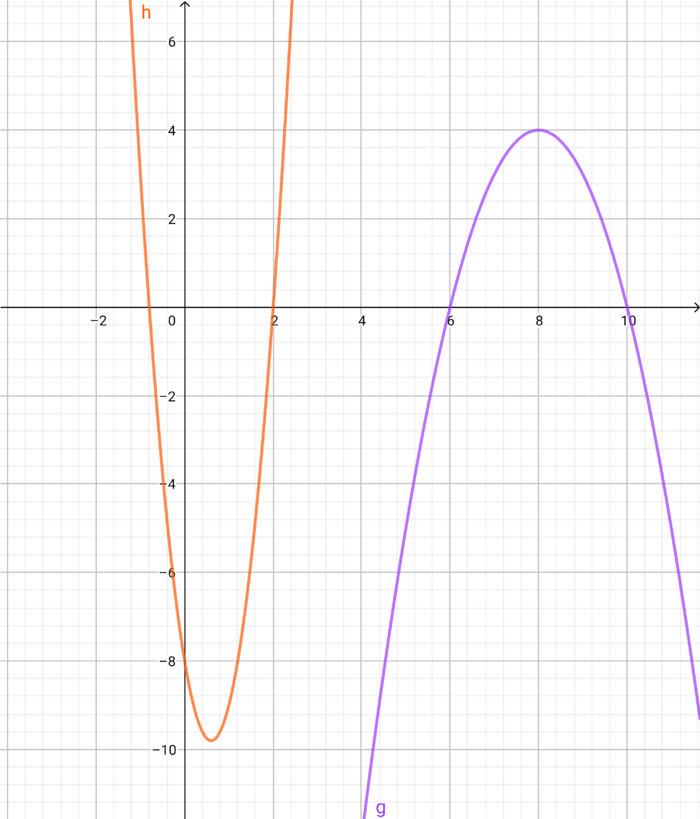
<math> g(x) = - 1 \cdot (x-8)^2+4 </math> <br /> | <math> g(x) = - 1 \cdot (x-8)^2+4 </math> <br /> | ||
<math> h(x) = 5x^2-6x-8</math> <br /> | <math> h(x) = 5x^2-6x-8</math> <br /> | ||
Berechne von beiden Funktionen jeweils die Nullstellen. | Berechne von beiden Funktionen jeweils die Nullstellen.}} | ||
{{Lösung versteckt| 1= Denke über die Bedeutung einer Nullstelle nach. Was bedeutet es, wenn eine Funktion an einem Punkt eine Nullstelle besitzt? |2= Tipp 1|3=schließen}} | {{Lösung versteckt| 1= Denke über die Bedeutung einer Nullstelle nach. Was bedeutet es, wenn eine Funktion an einem Punkt eine Nullstelle besitzt? |2= Tipp 1|3=schließen}} | ||
| Zeile 45: | Zeile 48: | ||
&\Leftrightarrow& 0 &&=&& -1(x-8)^2+4 &\mid :(-1) \\ | &\Leftrightarrow& 0 &&=&& -1(x-8)^2+4 &\mid :(-1) \\ | ||
&\Leftrightarrow& 0 &&=&& (x-8)^2-4 &\mid +4 \\ | &\Leftrightarrow& 0 &&=&& (x-8)^2-4 &\mid +4 \\ | ||
&\Leftrightarrow& 4 &&=&& (x-8)^2 | &\Leftrightarrow& 4 &&=&& (x-8)^2 & \mid \pm\sqrt{} \\ | ||
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 53: | Zeile 56: | ||
&\Rightarrow&(x_1-8) = 2& \textrm{sowie}& (x_2-8)=-2\\ | &\Rightarrow&(x_1-8) = 2& \textrm{sowie}& (x_2-8)=-2\\ | ||
\end{array} | \end{array} | ||
</math> |2= Lösung zu | </math> |2= Lösung zu g(x)| 3= schließen}} | ||
{{Lösung versteckt|1=<math>h(x) </math> liegt in Normalform vor. Es empfiehlt sich also die Funktion so umzuformen,so dass man die '''pq-Formel''' anwenden kann. | {{Lösung versteckt|1=<math>h(x) </math> liegt in Normalform vor. Es empfiehlt sich also die Funktion so umzuformen,so dass man die '''pq-Formel''' anwenden kann. | ||
| Zeile 60: | Zeile 63: | ||
Du erhälst die Gleichung <math>0 = x^2-\frac {6} {5} x-\frac{8}{5}</math><br /><br /> | Du erhälst die Gleichung <math>0 = x^2-\frac {6} {5} x-\frac{8}{5}</math><br /><br /> | ||
Durch Anwenden der pq-Formel folgt<br /><br /><br /> | Durch Anwenden der pq-Formel folgt<br /><br /><br /> | ||
<math> | |||
\begin{array} {rlll} | |||
|2= Lösung zu | &\Rightarrow&x_{1} = -\frac{-\frac{6}{5}}{2}-\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}& \textrm{sowie}& x_{2} = -\frac{-\frac{6}{5}}{2}+\sqrt{\left( -\frac{\frac{6}{5}}{2}\right)^2+\frac{8}{5}}\\ | ||
&\Rightarrow&x_1 = 0,8& \textrm{und}& x_2 = 2\\ | |||
\end{array} | |||
</math><br /> <br /><br /> | |||
|2= Lösung zu h(x) |3=schließen}} | |||
{{Lösung versteckt| 1= [[Datei:Graphische Lösung zur Nullstellenberechnung.png|700px|zentriert]] |2= Graphische Lösung | 3=schließen}} | |||
Aktuelle Version vom 30. Oktober 2019, 17:04 Uhr
Nullstellen
Ein Punkt wird als Nullstelle einer Funktion bezeichnet, wenn seine y-Koordinate gleich 0 ist.
D.h. um die Nullstellen einer Funktion zu bestimmen, solltest du die Funktion gleich 0 setzen.
Für die nächsten Schritte gibt es verschiedene Möglichkeiten vorzugehen:
Ist deine Funktion in Scheitelpunktform, so hilft es dir den Term auf einer Seite zu isolieren, um dann die Wurzel ziehen zu können.
liegt in Scheitelpunktform vor, weswegen eine Möglichkeit die Nullstellen zu bestimmen Folgende ist:
liegt in Normalform vor. Es empfiehlt sich also die Funktion so umzuformen,so dass man die pq-Formel anwenden kann.
Betrachte , d.h.
und führe dann eine Äquivalenzumformung durch, indem du durch 5 teilst.
Du erhälst die Gleichung
Durch Anwenden der pq-Formel folgt