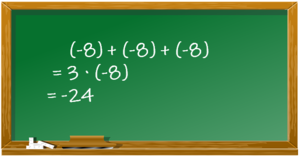Benutzer:Buss-Haskert/Rationale Zahlen 7E/Grundrechenarten Teil 2: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (17 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Arbeitsplan 4: Multiplizieren und Dividieren== | ==Arbeitsplan 4: Multiplizieren und Dividieren== | ||
===4. | ===4.1 Multiplikation von ganzen Zahlen=== | ||
Schau zunächst das einführende Video an:{{#ev:youtube|yEyB0608OiI|800|center}} | Schau zunächst das einführende Video an:{{#ev:youtube|yEyB0608OiI|800|center}} | ||
| Zeile 40: | Zeile 40: | ||
b) Was fällt dir auf? Notiere im Heft und vergleiche dein Ergebnis mit dem deines Nachbarn. | b) Was fällt dir auf? Notiere im Heft und vergleiche dein Ergebnis mit dem deines Nachbarn. | ||
Erinnerung: Kennst du dich aus mit den Fachbegriffen für die Multiplikation und Division? Löse das folgende Quiz:<div class="lueckentext-quiz | Erinnerung: Kennst du dich aus mit den Fachbegriffen für die Multiplikation und Division? Löse das folgende Quiz:<div class="lueckentext-quiz"> | ||
'''1. Faktor''' <big>∙</big> '''2. Faktor''' = Wert des '''Produktes''' | '''1. Faktor''' <big>∙</big> '''2. Faktor''' = Wert des '''Produktes''' | ||
| Zeile 51: | Zeile 51: | ||
'''3''' <big>∙</big> (-8) = -24 | '''3''' <big>∙</big> (-8) = -24 | ||
'''-3''' <big>∙</big> '''8''' = -24 | '''-3''' <big>∙</big> '''8''' = -24</div> | ||
</div> | |||
{{Box|Multiplikation von rationalen Zahlen|Das Vorzeichen des Produktes ist abhängig von den Vorzeichen der einzelnen Faktoren.<br>Das Ergebnis ist positiv ('''+'''), wenn beide Faktoren die '''gleichen Vorzeichen''' haben.<br>Das Ergebnis ist negativ ('''-'''), wenn beide Faktoren '''verschiedene Vorzeichen''' haben.|Arbeitsmethode}} | |||
Auch hier gilt also die bekannte Eselsbrücke: | Auch hier gilt also die bekannte Eselsbrücke: | ||
{{Box|1=Eselsbrücke:|2=[[Datei:Burro-1295939 1280.png|links|70px]] | {{Box|1=Eselsbrücke:|2=[[Datei:Burro-1295939 1280.png|links|70px]] | ||
| Zeile 75: | Zeile 68: | ||
also '''<big>+ ∙ (-) = -</big>''' und '''<big>- ∙ (+) = -</big>'''<br> | also '''<big>+ ∙ (-) = -</big>''' und '''<big>- ∙ (+) = -</big>'''<br> | ||
|3=Arbeitsmethode}} | |3=Arbeitsmethode}} | ||
Zusammenfassendes Video:<br> | |||
{{#ev:youtube|bCffZc1w8kM|800|center|||start=0&end=179}} | |||
{{#ev:youtube|bCffZc1w8kM| | {{Box|Übung 1: Multiplikation|Löse die nachfolgenden LearningApps Nr. 1-5. Für die schnellen Rechner gibt es Sprinteraufgaben.|Üben}}{{LearningApp|app=p5qhuyvg319|width=100%|height=600px}} | ||
{{Box|Übung 2|Löse Buch | |||
* S. 138, Nr. 2 | |||
{{Box|Übung 1: Multiplikation|Löse die nachfolgenden LearningApps Nr. 1-5. Für die schnellen Rechner gibt es Sprinteraufgaben.|Üben}}{{LearningApp|app=p5qhuyvg319|width=100%|height=600px}}{{Box|Übung 2 | * S. 139, Nr. 3 [https://apps.zum.de/apps/40694 Quiz zu Nr. 3] | ||
* S. 139, Nr. 4|Üben}} | |||
{{Lösung versteckt|Prüfe deine Lösungen mithilfe des Quizzes|Vergleiche deine Lösungen zu Nr. 3|Verbergen}} | |||
{{Lösung versteckt|1=Schau den Tipp erneut an:<br> | |||
'''<big>+ ∙ (+) = + </big>'''<br> | |||
'''<big>- ∙ (-) = +</big>'''<br> | |||
'''<big>+ ∙ (-) = -</big>'''<br> | |||
'''<big>- ∙ (+) = -</big>'''<br> | |||
|2= Tipp zu Nr. 4|3=Verbergen}} | |||
===4.2 Multiplikation von rationalen Zahlen (Dezimalbrüche)=== | |||
Die Vorzeichenregeln gelten natürlich auch für die Multiplikation und Division von Dezimalbrüchen. | |||
Erinnerung: Dezimalbrüche multiplizieren | |||
Dezimalbrüche werden multipliziert, indem die Zahlen zunächst ohne Berücksichtigung des Kommas multipliziert werden. Dann setzt man das Komma im Ergebnis. Das Ergebnis hat so viele Nachkommastellen, wie beide Faktoren zusammen.<br> | |||
Video zum Kopfrechnen: | |||
{{#ev:youtube|OQ3KKZhJeN8|800|center|||start=27&end=163}} | |||
Video zum schriftlichen Multiplizieren:<br> | |||
{{#ev:youtube|2QfdWJMQpUU|800|center}} | |||
{{Box|Übung 3|Löse Buch | {{Box|Übung 3|Löse Buch | ||
* S. | * S. 139, Nr. 5 | ||
* S. 139, Nr. | * S. 139, Nr. 6 [https://apps.zum.de/apps/40716 Quiz zu Nr. 6] | ||
* S. 139, Nr. 8|Üben}} | |||
* S. 139, Nr. 8 | {{Lösung versteckt|Schau noch einmal das Video oben zur Multiplikation von Dezimalbrüchen (Wohin muss das Komma?).|Tipp zu Nr. 5|Schließen}} | ||
{{Lösung versteckt|Vergleiche deine Lösungen zu Nr. 5:<br> | |||
{{Lösung versteckt| | -440; -336; -336; -340; -162; -117; -99; -56; -51; -29,6; -23,5; -16,2; -15,4; -12,8; -9,8; -9,5; -10,5; 1,62; 18,2; 18,4; 58,5; 90; 110; 143; 180; 195; 209; 363|Vergleiche deine Lösungen Nr. 5|Schließen}} | ||
Sprinteraufgaben: | |||
{{LearningApp|app=pyka42ud320|width=100%|height=600px}} | |||
===4.3 Multiplikation von rationalen Zahlen (Brüche)=== | |||
Und schlussendlich gelten die Vorzeichenregeln natürlich auch für die Multiplikation Brüchen. | |||
Erinnerung: Brüche multiplizieren<br> | |||
Brüche werden multipliziert, indem Zähler mit Zähler und Nenner mit Nenner multipliziert werden. Denke daran, zuerst zu kürzen und dann das Ergebnis zu berechnen. | |||
{{#ev:youtube|4h03jLZSRpg|800|center|||start=0&end=115}} | |||
{{Box|Übung 4|Löse Buch | |||
* S. 139, Nr. 11|Üben}} | |||
{{Lösung versteckt|1=Schreibe die Aufgabe als Lückenaufgabe, wie bei Nr. 9:<br> | |||
a) __ ___ ∙(-3) = 1 <br> | |||
Welches Vorzeichen muss die einzusetzende Zahl haben? (Lösung: -)<br> | |||
Tipp: Schreibe alle Zahlen der Aufgabe als Brüche<br> | |||
-___ ∙ <math>\left (- \frac{3}{1} \right ) = \left ( \frac{1}{1} \right )</math><br> | |||
b) __ ___ ∙ <math>\left (- \frac{1}{2} \right )</math> = 4 <br> | |||
Welches Vorzeichen muss die einzusetzende Zahl haben? (Lösung: -)<br> | |||
Tipp: Schreibe alle Zahlen der Aufgabe als Brüche<br> | |||
-___ ∙ <math>\left (- \frac{1}{2} \right ) = \left ( \frac{4}{1} \right )</math><br>|2=Tipps zu Nr. 11|3=Schließen}} | |||
{{Box|Übung 5: Multiplikation von rationalen Zahlen (Brüche)|Löse die nachfolgenden LearningApps Nr. 1-3. Für die schnellen Rechner gibt es Sprinteraufgaben.|Üben}}{{LearningApp|app=pmsesh0y320|width=100%|height=600px}} | |||
Ergänzung: | |||
{{Box | |||
| 1 = Übung 5 | |||
| 2 = Aufgaben mit mehreren Faktoren<br>Berechne | |||
* a) 2∙3∙(-1)∙(-4) | * a) 2∙3∙(-1)∙(-4) | ||
* b) (-2)∙3∙(-1)∙(-4) | * b) (-2)∙3∙(-1)∙(-4) | ||
* c) (-2)∙(-2)∙(-2) = (-2)<sup>3</sup> | * c) (-2)∙(-2)∙(-2) = (-2)<sup>3</sup> | ||
* d) (-2)∙(-2)∙(-2)∙(-2) = (-2)<sup>4</sup><br> | * d) (-2)∙(-2)∙(-2)∙(-2) = (-2)<sup>4</sup><br> | ||
Was gilt für das Vorzeichen des Ergebnisses? Beschreibe deine Beobachtung und vergleiche deine Lösung mit der deines Nachbarn.|3=Üben}}{{Lösung versteckt|a) +24 | Was gilt für das Vorzeichen des Ergebnisses? Beschreibe deine Beobachtung und vergleiche deine Lösung mit der deines Nachbarn. | ||
Ist die Anzahl gerade, so ist das Ergebnis positiv.<br> | | 3 = Üben | ||
Ist die Anzahl ungerade, so ist das Ergebnis negativ.|Beobachtung|Verbergen}} | }} | ||
{{Lösung versteckt|a) 2∙3∙(-1)∙(-4) = 6∙(-1)∙(-4) = -6 ∙(-4) = +24<br> | |||
b) (-2)∙3∙(-1)∙(-4) = -6∙(-1)∙(-4) = 6∙(-4) = -24<br> | |||
c) (-2)∙(-2)∙(-2) = 4 ∙(-2) = -8<br> | |||
d) (-2)∙(-2)∙(-2)∙(-2) = 4∙(-2)∙(-2) = -8∙(-2) = +16|Vergleiche deine Lösungen|Verbergen}} | |||
{{Lösung versteckt|Das Vorzeichnen des Ergebnisses hängt ab von der Anzahl der negativen Faktoren.|Tipp zur Beobachtung|Verbergen}} | |||
{{Lösung versteckt|Das Vorzeichnen des Ergebnisses hängt ab von der Anzahl der negativen Faktoren:<br> | |||
Ist die Anzahl gerade, so ist das Ergebnis positiv. Beispiel: "(-)∙(-)∙(-)∙(-) = + "<br> | |||
Ist die Anzahl ungerade, so ist das Ergebnis negativ. Beispiel: "(-)∙(-)∙(-) = -"|Beobachtung|Verbergen}} | |||
===5.1) Division von ganzen Zahlen === | |||
Erinnerung: Kennst du dich aus mit den Fachbegriffen für Division? | |||
Löse das folgende Quiz: | |||
<div class="lueckentext-quiz"> | |||
'''Dividend''' <big>:</big> '''Divisor''' = Wert des '''Quotienten'''<br> | |||
Beispiele:<br> | |||
24 <big>:</big> '''3''' = 8<br> | |||
'''-24''' <big>:</big> (-3) = 8<br> | |||
'''24''' <big>:</big>(-3) = -8<br> | |||
'''-24''' <big>:</big> '''3''' = -8 | |||
</div><br><br /> | |||
{{Box|Division von rationalen Zahlen|Das Vorzeichen des Quotienten ist abhängig von den Vorzeichen von Dividend und Divisor.<br>Das Ergebnis ist positiv ('''+'''), wenn beide Zahlen die '''gleichen Vorzeichen''' haben.<br>Das Ergebnis ist negativ ('''-'''), wenn beide Zahlen '''verschiedene Vorzeichen''' haben.|Arbeitsmethode}} | |||
Auch hier gilt also die bekannte Eselsbrücke: | |||
{{Box|1=Eselsbrücke:|2=[[Datei:Burro-1295939 1280.png|links|70px]] | |||
'''<big>+ : (+) = + </big>'''<br> | |||
'''<big>- : (-) = +</big>'''<br> | |||
'''<big>+ : (-) = -</big>'''<br> | |||
'''<big>- : (+) = -</big>'''<br></div> | |||
Merke dir diese Regel mit dem Memoryspiel:<br> | |||
[[Datei:Memory Kurzschreibweise.png|rechts|150px]]Wenn du zwei gleiche Karten aufdeckst, freust du dich (+),<br> | |||
also '''<big>+ : (+) = + </big>''' und '''<big>- : (-) = +</big>'''<br> | |||
wenn du verschiedene Karten aufdeckst, bist du traurig (-),<br> | |||
also '''<big>+ : (-) = -</big>''' und '''<big>- : (+) = -</big>'''<br> | |||
|3=Arbeitsmethode}} | |||
{{#ev:youtube|9t6niouU4BQ|460|center|||start=0&end=130}} | |||
{{Box|Übung 6: Division|Löse die nachfolgenden LearningApps Nr. 1-5. Für die schnellen Rechner gibt es Sprinteraufgaben.|Üben}} | |||
{{LearningApp|app=p7rhdskhn19|width=100%|height=600px}} | |||
{{Box|Übung 7|Löse Buch | |||
* S. 140, Nr. 4 | |||
* S. 140, Nr. 5|Üben}} | |||
===5.1) Division von rationalen Zahlen (Dezimalbrüche) === | |||
Erinnerung: Dezimalbrüche dividieren | Erinnerung: Dezimalbrüche dividieren | ||
Beim Dividieren von Dezimalbrüchen durch eine ganze Zahl wird das Ergebnis im Komma gesetzt, sobald das Komma beim Dividenden überschritten wird. Ist der Divisor auch ein Dezimalbruch, müssen zunächst beim Dividenden und beim Divisor das Komma um so viele Stellen nach rechts verschoben werden, bis der Divisor eine natürliche Zahl ist. | Beim Dividieren von Dezimalbrüchen durch eine ganze Zahl wird das Ergebnis im Komma gesetzt, sobald das Komma beim Dividenden überschritten wird. Ist der Divisor auch ein Dezimalbruch, müssen zunächst beim Dividenden und beim Divisor das Komma um so viele Stellen nach rechts verschoben werden, bis der Divisor eine natürliche Zahl ist.<br> | ||
Wiederholung:<br> | |||
{{#ev:youtube|PVHoyFOYtBs|800|center|||start=0&end=402}} | |||
{{ | |||
{{Box|Übung 8: Division von rationalen Zahlen (Dezimalbrüche)|Löse die nachfolgenden LearningApps Nr. 1-3. Für die schnellen Rechner gibt es Sprinteraufgaben.|Üben}}{{LearningApp|app=pe5ngm31k20|width=100%|height=600px}} | |||
{{Box|Übung 9|Löse Buch | |||
* S. 141, Nr. 9 (Ich würde vorschlagen, zunächst die Aufgaben von Übung 10 zu lösen und dann diese Aufgabe.)|Üben}} | |||
{{Box|Übung 10|Löse Buch | |||
* S. 141, Nr. 10 | |||
* S. 141, Nr. 11 | |||
* S. 141, Nr. 8|Üben}} | |||
{{Box|Übung | {{Box|Übung 11|Löse Buch | ||
* S. 147, Nr. 3 | |||
* S. 147, Nr. 4 | |||
* S. 147, Nr. 6 | |||
* S. 146, Nr. 27 | |||
* S. 146, Nr. 29 | |||
* S. 146, Nr. 30 | |||
* S. 147, Nr.1|Üben}} | |||
===5.3) Multiplikation und Division von rationalen Zahlen (Brüche)=== | |||
Und schlussendlich gelten die Vorzeichenregeln natürlich auch für die Division von Brüchen.<br> | |||
Brüche werden dividiert, indem der erste Bruch mit dem Kehrbruch des zweiten Bruches multipliziert wird. ("Schweinchenlied") | Brüche werden dividiert, indem der erste Bruch mit dem Kehrbruch des zweiten Bruches multipliziert wird. ("Schweinchenlied") | ||
{{#ev:youtube|YTdMsLPwTVY|800|center}} | |||
{{Box|1=Weitere Übungen|2=Hier kannst du bei Bedarf weiter üben: | |||
* [https://mathe.aufgabenfuchs.de/rationale-zahlen/rationale-zahlen.shtml '''Aufgabenfuchs Aufgabe 52-58'''] | |||
* [https://mathe.aufgabenfuchs.de/rationale-zahlen/rationale-zahlen.shtml '''Aufgabenfuchs Aufgabe 59-60'''] | |||
* Wähle in den Applets die Rechenart, die du üben möchtest, aus. | |||
<ggb_applet id="mgE9jkgt" width="600" height="230" border="888888" /><br> | |||
Applet von Wolfgang Wengler<br> | |||
<ggb_applet id="BnZhTbY3" width="726" height="375" border="888888" /> | |||
Applet von Tinwing|3=Üben}} | |||
Aktuelle Version vom 9. April 2025, 19:24 Uhr
Arbeitsplan 4: Multiplizieren und Dividieren
4.1 Multiplikation von ganzen Zahlen
Schau zunächst das einführende Video an:
Jana hat eine Aufgabe an der Tafel gerechnet:
Aufgabe 1
a) Gib eine Situation an, die zu Janas Rechnung passt (Tipp: Erinnere dich an die Situation im Video)
b) Beschreibe, wie sie bei ihrer Rechnung vorgegangen ist.
c) Löse ebenso:
(-2)+(-2)+(-2)+(-2)
= ...
(-5)+(-5)+(-5)
= ...
(-3)+(-3)+(-3)+(-3)+(-3)+(-3)+(-3)+(-3)
=
d) Was fällt dir auf? Notiere im Heft und vergleiche dein Ergebnis mit dem deines Nachbarn.
Aufgabe 2
Nun sollst du an der Tafel rechnen:
a) Schreibe die Aufgabenfolgen in dein Heft und ergänze die Lücken.
b) Was fällt dir auf? Notiere im Heft und vergleiche dein Ergebnis mit dem deines Nachbarn.
Erinnerung: Kennst du dich aus mit den Fachbegriffen für die Multiplikation und Division? Löse das folgende Quiz:
1. Faktor ∙ 2. Faktor = Wert des Produktes
Beispiele:
3 ∙ 8 = 24
-3 ∙ (-8) = 24
3 ∙ (-8) = -24
-3 ∙ 8 = -24
Auch hier gilt also die bekannte Eselsbrücke:
Zusammenfassendes Video:
Schau den Tipp erneut an:
+ ∙ (+) = +
- ∙ (-) = +
+ ∙ (-) = -
4.2 Multiplikation von rationalen Zahlen (Dezimalbrüche)
Die Vorzeichenregeln gelten natürlich auch für die Multiplikation und Division von Dezimalbrüchen.
Erinnerung: Dezimalbrüche multiplizieren
Dezimalbrüche werden multipliziert, indem die Zahlen zunächst ohne Berücksichtigung des Kommas multipliziert werden. Dann setzt man das Komma im Ergebnis. Das Ergebnis hat so viele Nachkommastellen, wie beide Faktoren zusammen.
Video zum Kopfrechnen:
Video zum schriftlichen Multiplizieren:
Vergleiche deine Lösungen zu Nr. 5:
Sprinteraufgaben:
4.3 Multiplikation von rationalen Zahlen (Brüche)
Und schlussendlich gelten die Vorzeichenregeln natürlich auch für die Multiplikation Brüchen.
Erinnerung: Brüche multiplizieren
Brüche werden multipliziert, indem Zähler mit Zähler und Nenner mit Nenner multipliziert werden. Denke daran, zuerst zu kürzen und dann das Ergebnis zu berechnen.
Schreibe die Aufgabe als Lückenaufgabe, wie bei Nr. 9:
a) __ ___ ∙(-3) = 1
Welches Vorzeichen muss die einzusetzende Zahl haben? (Lösung: -)
Tipp: Schreibe alle Zahlen der Aufgabe als Brüche
-___ ∙
b) __ ___ ∙ = 4
Welches Vorzeichen muss die einzusetzende Zahl haben? (Lösung: -)
Tipp: Schreibe alle Zahlen der Aufgabe als Brüche
Ergänzung:
5.1) Division von ganzen Zahlen
Erinnerung: Kennst du dich aus mit den Fachbegriffen für Division? Löse das folgende Quiz:
Dividend : Divisor = Wert des Quotienten
Beispiele:
24 : 3 = 8
-24 : (-3) = 8
24 :(-3) = -8
-24 : 3 = -8
Auch hier gilt also die bekannte Eselsbrücke:
5.1) Division von rationalen Zahlen (Dezimalbrüche)
Erinnerung: Dezimalbrüche dividieren
Beim Dividieren von Dezimalbrüchen durch eine ganze Zahl wird das Ergebnis im Komma gesetzt, sobald das Komma beim Dividenden überschritten wird. Ist der Divisor auch ein Dezimalbruch, müssen zunächst beim Dividenden und beim Divisor das Komma um so viele Stellen nach rechts verschoben werden, bis der Divisor eine natürliche Zahl ist.
Wiederholung:
5.3) Multiplikation und Division von rationalen Zahlen (Brüche)
Und schlussendlich gelten die Vorzeichenregeln natürlich auch für die Division von Brüchen.
Brüche werden dividiert, indem der erste Bruch mit dem Kehrbruch des zweiten Bruches multipliziert wird. ("Schweinchenlied")