Benutzer:Stoll-Gym10Erfurt/Mathematik10/Trigonometrische Funktionen: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: Quelltext-Bearbeitung 2017
Keine Bearbeitungszusammenfassung
Markierung: Quelltext-Bearbeitung 2017
 
(19 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 16: Zeile 16:
|Icon= <span class="brainy hdg-screen01"></span>    
|Icon= <span class="brainy hdg-screen01"></span>    
}}
}}
=== Der Einfluss von Parametern in der Funktion <math>y=f(x)=a \cdot sin(b \cdot(x-c))+d </math>===
=== Der Einfluss von Parametern in der Funktion <math>y=f(x)=a \cdot sin(b \cdot(x-c))+d </math>===
{{Box-spezial
{{Box-spezial
Zeile 35: Zeile 36:
{{Box-spezial
{{Box-spezial
|Titel= Interaktive Übung
|Titel= Interaktive Übung
|Inhalt= [https://realmath.de/Neues/Klasse10/trifkt/sinusfunktionvar.php Übung im Internet]  
|Inhalt= [https://realmath.de/Neues/Klasse10/trifkt/sinusfunktionvar.php Einfluss der Parameter grafisch nachvollziehen]  
|Farbe= #0077dd       
|Farbe= #0077dd       
|Hintergrund= #A8DF4A
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-dinosaur"></span>     
|Icon= <span class="brainy hdg-dinosaur"></span>     
}}
{{Box-spezial
|Titel= Merke
|Inhalt= <big> Die allgemeine Funktionsgleichung für die Sinusfunktion lautet:
<math>f(x)=a\cdot sin(b\cdot(x-c))+d </math></big><br/>
Dabei haben die Parameter folgende Bedeutung:
* '''a''' - Einfluss auf die Amplitude (Amplitude - Entfernung von-Achse bis zum Hoch- oder Tiefpunkt oder einfach auch "Berg- und Talspitze"). Man spricht auch von Streckung oder Stauchung in y-Richtung. Wenn a < 0 erfolgt eine Spiegelung an der x-Achse.
* '''b''' - Veränderung der Periode p (Periode - Eine komplette Auf- und Abwärtsbewegung oder Abstand zwischen zwei Bergspitzen)
<math>\qquad</math> Es gilt folgende Gleichung für die Periode: <math>p=\frac{2\pi}{b} </math>.<br/>
<math>\qquad</math> Somit ergeben sich folgende Zusammenhänge: <math>b=1 \rightarrow p=2\pi, b=2 \rightarrow p=\pi, b=4 \rightarrow p=\frac{\pi}{2} </math>
* '''c''' - Verschiebung in x-Richtung; c > 0 nach rechts, c < 0 nach links
* '''d''' - Verschiebung in y-Richtung; d > 0 nach oben, c < 0 nach unten
|Farbe= #FF0000
|Hintergrund= #00FF00
|Icon= <span class="brainy hdg-graduation-hat"></span>
}}
{{Box-spezial
|Titel= Zusammenfassung und Aufgaben
|Inhalt= Lade auf Dein iPad die [https://projekte.zum.de/images/6/6a/Ma10_-_Sinus-Funktion_Wissen_und_Beispiele.pdf Datei], speichere sie und löse auch die Aufgaben der zweiten Seite.
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class="brainy hdg-tablet06"></span>
}}
}}
=== Übungen auf Learningapp.org ===
=== Übungen auf Learningapp.org ===
Zeile 49: Zeile 72:
|Icon= <span class=" brainy hdg-pin "></span>
|Icon= <span class=" brainy hdg-pin "></span>
}}
}}
 
{{Box-spezial
 
|Titel= Übung 2
 
|Inhalt= <big>Wähle richtig aus.</big>
{{Box|Übung 2: Finde passende Pärchen.<br/>
{{LearningApp|app= 1504620|width=100%|height=650px}}
{{LearningApp|app= 1504620|width=100%|height=650px}}
|
|Farbe= #0077dd
|Arbeitsmethode}}
|Hintergrund= #A8DF4A
<br />
|Icon= <span class=" brainy hdg-pin "></span>
{{Box|Übung 3: Finde passende Pärchen.<br/>
}}
{{Box-spezial
|Titel= Übung 3
|Inhalt= <big>Finde passende Pärchen.</big>
{{LearningApp|app= 7360531|width=100%|height=500px}}
{{LearningApp|app= 7360531|width=100%|height=500px}}
|
|Farbe= #0077dd
|Arbeitsmethode}}
|Hintergrund= #A8DF4A
<br />
|Icon= <span class=" brainy hdg-pin "></span>
 
}}
{{Box|Übung 4: Finde passende Pärchen.<br/>
{{Box-spezial
|Titel= Übung 4
|Inhalt= <big>Bestimme die Parameter.</big>
{{LearningApp|app= 2535067|width=100%|height=530px}}
{{LearningApp|app= 2535067|width=100%|height=530px}}
|
|Farbe= #0077dd
|Arbeitsmethode}}
|Hintergrund= #A8DF4A
<br />
|Icon= <span class=" brainy hdg-pin "></span>
{{Box|Übung 5: Finde passende Pärchen.<br/>
}}
{{Box-spezial
|Titel= Übung 5
|Inhalt= <big>Bestimme die Parameter.</big>
{{LearningApp|app= 2535077|width=100%|height=530px}}
{{LearningApp|app= 2535077|width=100%|height=530px}}
|
|Farbe= #0077dd
|Arbeitsmethode}}
|Hintergrund= #A8DF4A
<br />
|Icon= <span class=" brainy hdg-pin "></span>
}}
{{Box-spezial
|Titel= Übung 6
|Inhalt= <big>Mehrere Übungen in einer App</big>
{{LearningApp|app= 14818774|width=100%|height=530px}}
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class=" brainy hdg-pin "></span>
}}


===Aufgaben===
===Aufgaben===
{{Box|Die Abbildung zeigt die Graphen von drei Sinusfunktionen. Bestimme die Gleichungen. |2=
{{Box-spezial
|Titel= Aufgabe
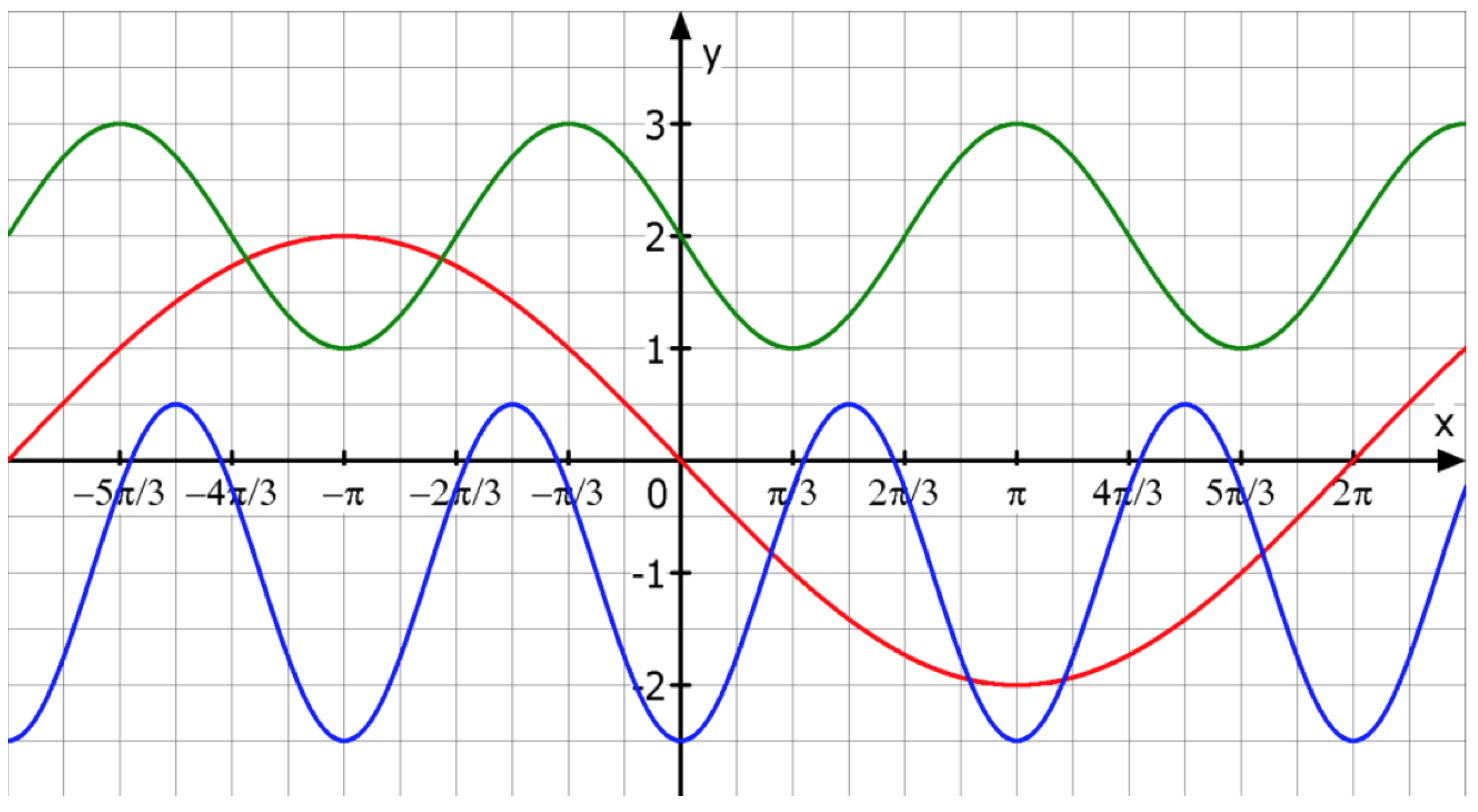
|Inhalt= <big>Die Abbildung zeigt die Graphen von drei Sinusfunktionen. Bestimme die Gleichungen.</big>
[[Datei:Sinusfunktionen.png]]
[[Datei:Sinusfunktionen.png]]
{{Lösung versteckt|1 = roter Graph:<math>\; f(x) = 2 \cdot sin(0,5x+\pi)</math> <br/>
{{Lösung versteckt|1 = roter Graph:<math>\; f(x) = 2 \cdot sin(0,5x+\pi)</math> <br/>
blauer Graph:<math>\; f(x) = -1,5 \cdot sin(2x+\frac{\pi}{2})-1</math> <br/>
blauer Graph:<math>\; f(x) = -1,5 \cdot sin(2x+\frac{\pi}{2})-1</math> <br/>
grüner Graph:<math>\;f(x) = sin(1,5x - \pi)+2</math>}}
grüner Graph:<math>\;f(x) = sin(1,5x - \pi)+2</math>}}
|3=Üben}}
|Farbe= #0077dd
|Hintergrund= #A8DF4A
|Icon= <span class=" brainy hdg-pin "></span>
}}
{{Box-spezial
{{Box-spezial
|Titel= Video zum Lösen trigonometrischer Gleichungen
|Titel= Video zum Lösen trigonometrischer Gleichungen

Aktuelle Version vom 5. Mai 2025, 15:22 Uhr

Die Sinus- und die Cosinusfunktion

Übung 1

Sieh Dir im Geogebra Applet an, wie am Einheitskreis die Sinus-, Kosinus- bzw. die Tangensfunktion entsteht. Wähle eine der drei Funktionen aus und betätige den Play-Button in der linken unteren Ecke.

GeoGebra
    Die Sinus- und Kosinusfunktion

Umfassender Einstieg

Video laden
YouTube

Der Einfluss von Parametern in der Funktion

    Die Sinusfunktion

Einfluss der Parameter I

Video laden
YouTube

    Die Sinusfunktion

Einfluss der Parameter II

Video laden
YouTube

Merke

Die allgemeine Funktionsgleichung für die Sinusfunktion lautet:
Dabei haben die Parameter folgende Bedeutung:

  • a - Einfluss auf die Amplitude (Amplitude - Entfernung von-Achse bis zum Hoch- oder Tiefpunkt oder einfach auch "Berg- und Talspitze"). Man spricht auch von Streckung oder Stauchung in y-Richtung. Wenn a < 0 erfolgt eine Spiegelung an der x-Achse.
  • b - Veränderung der Periode p (Periode - Eine komplette Auf- und Abwärtsbewegung oder Abstand zwischen zwei Bergspitzen)

Es gilt folgende Gleichung für die Periode: .
Somit ergeben sich folgende Zusammenhänge:

  • c - Verschiebung in x-Richtung; c > 0 nach rechts, c < 0 nach links
  • d - Verschiebung in y-Richtung; d > 0 nach oben, c < 0 nach unten
Zusammenfassung und Aufgaben
Lade auf Dein iPad die Datei, speichere sie und löse auch die Aufgaben der zweiten Seite.

Übungen auf Learningapp.org

Übung 1

Finde passende Pärchen.

Übung 2

Wähle richtig aus.

Übung 3

Finde passende Pärchen.

Übung 4

Bestimme die Parameter.

Übung 5

Bestimme die Parameter.

Übung 6

Mehrere Übungen in einer App

Aufgaben

Aufgabe

Die Abbildung zeigt die Graphen von drei Sinusfunktionen. Bestimme die Gleichungen. Sinusfunktionen.png

roter Graph:
blauer Graph:

grüner Graph:
    Video zum Lösen trigonometrischer Gleichungen

Vorrechnen einer Aufgabe

Video laden
YouTube

Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Stoll-Gym10Erfurt/Mathematik10/Trigonometrische_Funktionen&oldid=104049“