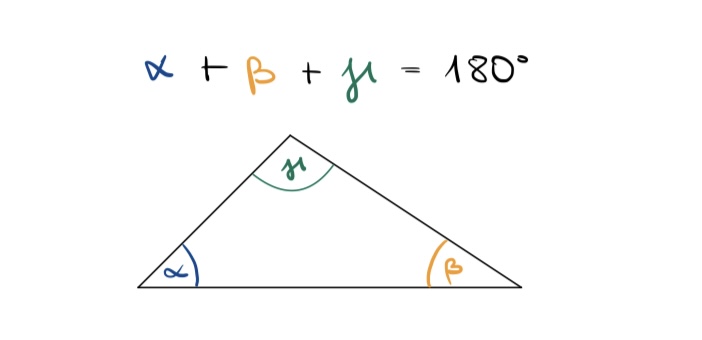|
|
| Zeile 22: |
Zeile 22: |
|
| |
|
| Du kannst dies auch an dem GeoGebra Applet ausprobieren und beobachten, ob das auch bei verschiedenen Dreiecken klappt! | | Du kannst dies auch an dem GeoGebra Applet ausprobieren und beobachten, ob das auch bei verschiedenen Dreiecken klappt! |
| <ggb_applet id="b8amsbc2" width="1060" height="580" border="888888" smb="true" stb="true" ai="true" asb="true" /> | | <ggb_applet id="b8amsbc2" width="657" height="360" border="888888" /> |
| == Fair Play im Ecken-Fußball: Ein geometrisches Problem im Sportunterricht == | | == Fair Play im Ecken-Fußball: Ein geometrisches Problem im Sportunterricht == |
| {{Box|1=Winkelberechnung im Ecken-Fußball mit dem Innenwinkelsatz|2=Die Klasse 8a spielt in der Sportstunde ein Spiel namens Ecken-Fußball. Dafür stellen sie ein Dreieck aus Bänken auf, bei dem jede Ecke ein Tor darstellt. Der Kapitän von Mannschaft A behauptet, dass das Tor von Mannschaft C viel kleiner ist als die anderen. Die Sportlehrerin beruhigt die Klasse und erklärt:,,Ich kann euch versichern, dass das Tor von Mannschaft A einen Winkel von 60° hat und das Tor von Mannschaft B genauso groß ist. Mit eurem Wissen aus dem Mathematikunterricht solltet ihr herausfinden, ob das Tor von Mannschaft C größer oder kleiner ist als die anderen.'' | | {{Box|1=Winkelberechnung im Ecken-Fußball mit dem Innenwinkelsatz|2=Die Klasse 8a spielt in der Sportstunde ein Spiel namens Ecken-Fußball. Dafür stellen sie ein Dreieck aus Bänken auf, bei dem jede Ecke ein Tor darstellt. Der Kapitän von Mannschaft A behauptet, dass das Tor von Mannschaft C viel kleiner ist als die anderen. Die Sportlehrerin beruhigt die Klasse und erklärt:,,Ich kann euch versichern, dass das Tor von Mannschaft A einen Winkel von 60° hat und das Tor von Mannschaft B genauso groß ist. Mit eurem Wissen aus dem Mathematikunterricht solltet ihr herausfinden, ob das Tor von Mannschaft C größer oder kleiner ist als die anderen.'' |
Version vom 14. November 2024, 23:25 Uhr
Informationskästchen
Info
In diesem Lernpfadkapitel tauchen wir in die spannende Welt der Dreiecke ein und erforschen die Geheimnisse der Innenwinkelsumme.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Viel Erfolg!
Einführung
Was ist die Innenwinkelsumme in einem Dreieck?
Die Summe der Innenwinkel in einem Dreieck beträgt immer 180 Grad. Dies wird durch den Innenwinkelsatz beschrieben.
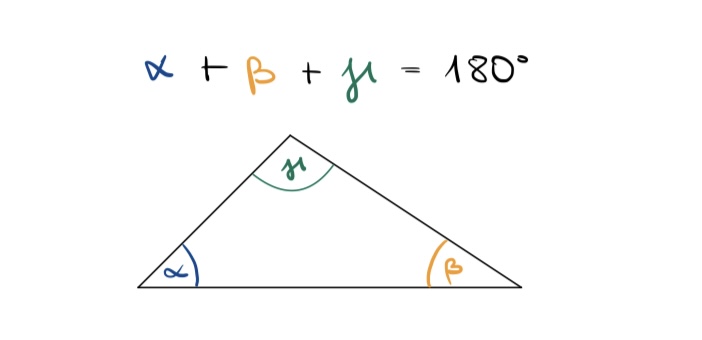
Stimmt das auch wirklich?
Wenn ja, dann müssten die drei Innenwinkel im Dreieck einen gestreckten Winkel ergeben.
Das sollte dann also in etwa so aussehen:
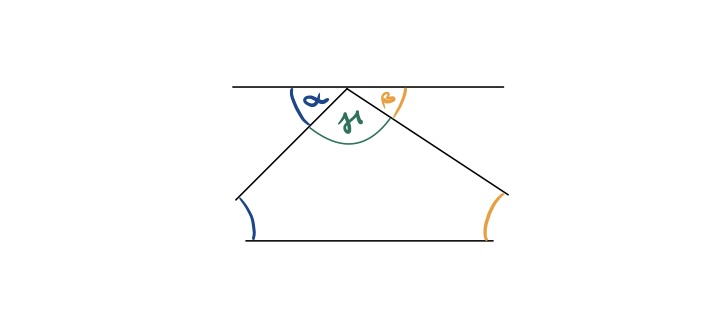
Reiße die zwei Winkel α und β deines Dreiecks (auf dem Arbeitsblatt) ab und prüfe, ob man sie an der Spitze zu einem gestreckten Winkel mit 180° anordnen kann.
Du kannst dies auch an dem GeoGebra Applet ausprobieren und beobachten, ob das auch bei verschiedenen Dreiecken klappt!
Fair Play im Ecken-Fußball: Ein geometrisches Problem im Sportunterricht
Winkelberechnung im Ecken-Fußball mit dem Innenwinkelsatz
Die Klasse 8a spielt in der Sportstunde ein Spiel namens Ecken-Fußball. Dafür stellen sie ein Dreieck aus Bänken auf, bei dem jede Ecke ein Tor darstellt. Der Kapitän von Mannschaft A behauptet, dass das Tor von Mannschaft C viel kleiner ist als die anderen. Die Sportlehrerin beruhigt die Klasse und erklärt:,,Ich kann euch versichern, dass das Tor von Mannschaft A einen Winkel von 60° hat und das Tor von Mannschaft B genauso groß ist. Mit eurem Wissen aus dem Mathematikunterricht solltet ihr herausfinden, ob das Tor von Mannschaft C größer oder kleiner ist als die anderen.
Hilf der Klasse 8a, indem du den Winkel des Tores von Mannschaft C berechnest und begründe deine Antwort. Ist das Fußballspiel fair oder nicht?
Zusatzfrage
Wenn das Spielfeld so geändert wird, dass der Winkel des Tores von Mannschaft A auf 70° vergrößert wird, wie verändert sich der Winkel des Tores von Mannschaft C? Begründe, ob das Spiel fair ist oder nicht.
Aufgabe 1
Level 1: Erstere Hinweise
Euer erster Hinweis führt euch zu einem Dreieck, bei dem zwei Winkel gegeben sind: 50° und 60°. Der dritte Winkel ist jedoch verdeckt. Findet den verborgenen Winkel und zeigt rechnerisch, dass die Summe der Innenwinkel 180° beträgt. Die Innenwinkelsumme eines Dreiecks ist immer 180°, weil die drei Winkel zusammen eine gerade Linie ergeben, wenn man sie nebeneinanderlegt. Eine gerade Linie hat immer 180°.
Level 2: Weitere Spuren entdecken
Euer nächster Hinweis befindet sich in einem gleichschenkligen Dreieck. Ihr wisst, dass die beiden Basiswinkel jeweils 65° betragen, aber der Winkel an der Spitze ist unleserlich. Berechnet diesen Winkel und erklärt rechnerisch, warum die Innenwinkelsumme 180° ergibt. Argumentiert, warum die Summe der Winkel im Dreieck immer diese Zahl ergibt, egal wie das Dreieck aussieht.
Level 3: Das letzte Rätsel
Auf dem letzten Teil eurer Jagd entdeckt ihr eine mysteriöse geometrische Nachricht: "In jedem Dreieck steht ein gestreckter Winkel, wenn man die Innenwinkel nebeneinanderlegt." Ihr sollt dies überprüfen, in dem ihr ein eigenes Dreieck konstruiert und die drei Innenwinkel nebeneinander anordnet. Zeigt, dass diese Winkel zusammen einen gestreckten Winkel (180°) ergeben und begründet rechnerisch und logisch, warum dies immer so ist.
Zusatzfrage: Überlegt, ob diese Regel auch für Vierecke gilt und begründet eure Antwort.
Aufgabe 2
Aufgabe 2.1
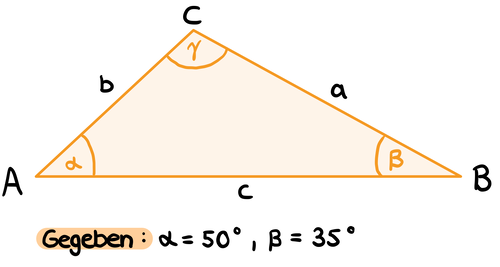
Berechne den fehlenden Winkel mithilfe des Innenwinkelsatzes!
Berechne den fehlenden Winkel γ, indem du die Winkel α und β von 180° abziehst.
Aufgabe 2.2
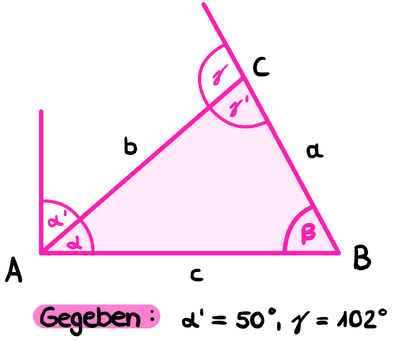
Erkenne die Innenwinkel des Dreiecks und berechne sie!
α und α' bilden einen rechten Winkel. Es gilt also α+α'=90°. Wie kannst du herausfinden, wie groß α ist?
γ und γ' sind Nebenwinkel. Es gilt also γ+γ'=180°. Wie kannst du herausfinden, wie groß γ' ist?
Berechne den fehlenden Winkel β mithilfe des Innenwinkelsatzes!
Aufgabe 2.3
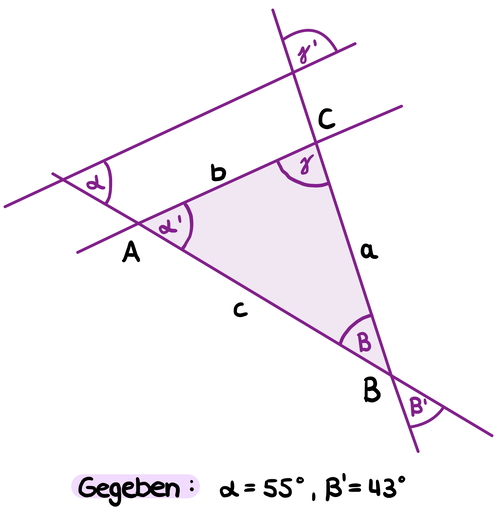
Bestimme die Innenwinkel des Dreiecks!
α und α' sind Stufenwinkel. Wie groß ist dann α'?
β und β' sind Scheitelwinkel. Wie groß ist dann β?
Berechne den fehlenden Winkel γ mithilfe des Innenwinkelsatzes!
Aufgabe 3
Aufgabe 4 (Sicherung)
Hier kommst du zurück zur Startseite des Kapitels: Geometrie im Dreieck