Benutzer:Buss-Haskert/Daten/Daten auswerten: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (24 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
SEITE IM AUFBAU! | |||
{{Navigation|[[Benutzer:Buss-Haskert/Daten|Vorwissen]]<br> | |||
[[Benutzer:Buss-Haskert/Daten/Daten auswerten|3) Daten auswerten (Kennwerte)]]<br> | |||
[[Benutzer:Buss-Haskert/Daten/Daten darstellen|4) Daten darstellen (Boxplots)]]}} | |||
{{Box|Flohsprung|[[Datei:Game-g821282aec 1920.jpg|rechts|rahmenlos|200x200px]]Wir führen das Experiment FLOHSPRUNG durch: | {{Box|Flohsprung|[[Datei:Game-g821282aec 1920.jpg|rechts|rahmenlos|200x200px]]Wir führen das Experiment FLOHSPRUNG durch: | ||
Arbeitet in euren Tischgruppen zusammen: | Arbeitet in euren Tischgruppen zusammen: | ||
| Zeile 14: | Zeile 21: | ||
* Wie weit kommt der beste Sprung? | * Wie weit kommt der beste Sprung? | ||
* Vergleich die Mittelwerte der Flohsprünge.|Frage}} | * Vergleich die Mittelwerte der Flohsprünge.|Frage}} | ||
Wiederhole zunächst noch einmal die Begriffe: Urliste, Rangliste, Zentralwert (Median) und Mittelwert (Durchschnitt). | |||
{{#ev:youtube|IFJKMF4uYcQ|800|center|||start=224&end=510}} | |||
{{LearningApp|app=pp9a6p5i321|width=100%|height=400px}} | |||
{{LearningApp|app=10783987|with=100%|height=600px}} | |||
{{LearningApp|app=17567656|width=100%|height=600px}} | |||
{{Box|Übung 1|Löse auf der Seite [https://mathe.aufgabenfuchs.de/wahrscheinlichkeit/relative-haeufigkeit.shtml '''Aufgabenfuchs'''] die nachfolgenden Aufgaben:<br> | |||
Urliste, Rangliste, Kennwerte (Minimum, Maximum, Zentralwert, Spannweite, Mittelwert): | |||
* Nr. 1 bis Nr. 9 | |||
Relative Häufigkeit | |||
* Nr. 10 bis 23|Üben}} | |||
Nun noch einmal die obige Aufgabe: | |||
{{Box|Frage zur Auswerung in der Gruppe|* Wer ist am besten im "Flohsprung"? | |||
* Wer hat gleichbleibend gute Werte? | |||
* Wie weit kommt der schlechteste Sprung maximal? | |||
* Wie weit kommt der beste Sprung? | |||
* Vergleich die Mittelwerte der Flohsprünge.|Frage}} | |||
{{Lösung versteckt|1=Als Beispiel findest du hier die Werte von Tim und Tina.<br> | |||
[[Datei:Boxplot Flohsprung Beispiel Tabelle.jpg|rahmenlos|600px]]<br> | |||
* schlechtester Sprung (Minimum): Tim 7 cm; Tina 4 cm<br> | |||
* bester Sprung (Maximum): Tim: 84 cm; Tina 109 cm<br> | |||
* Mittelwerte (arithmetisches Mittel): <br> | |||
Tim: <math>\bar{a} = \tfrac{7+8+12+15+17+18+24+25+28+30+35+42+70+83+84}{15} =\tfrac{498}{15} = 33,2 (cm)</math><br> | |||
Tina: <math>\bar{a} = \tfrac{4+17+18+18+25+27+30+30+32+48+60+71+73+75+85+100+101+109}{18} =\tfrac{923}{18} = 51,3 (cm)</math><br> | |||
* Median (Zentralwert): <br> | |||
Tim Rang: <math>\tfrac{15}{2}</math> = 7,5, also Rang 8: 25 cm<br> | |||
Tina Rang: <math>\tfrac{18}{2}</math> = 9, also Mittelwert des 9. und 10. Ranges: <math>\tfrac{32+48}{2} = \tfrac{80}{2} = 40 (cm)</math>|2=Beispielrechnungen für zwei Tabellen|3=Verbergen}} | |||
<br> | |||
Um diese Daten auszuwerten, helfen die dir schon bekannten Kennwerte: | Um diese Daten auszuwerten, helfen die dir schon bekannten Kennwerte: | ||
| Zeile 20: | Zeile 57: | ||
{{!}} Kennwert | {{!}} Kennwert | ||
{{!}} Beschreibung | {{!}} Beschreibung | ||
{{!-}} | |||
{{!}} Minimum | {{!}} Minimum | ||
{{!}} Der kleinste Wert der Rangliste heißt Minimum. | {{!}} Der kleinste Wert der Rangliste heißt Minimum. | ||
{{! | {{!-}} | ||
{{!}} Maximum | {{!}} Maximum | ||
{{!}} Der größte Wert der Rangliste heißt Maximum. | {{!}} Der größte Wert der Rangliste heißt Maximum. | ||
{{! | {{!-}} | ||
{{!}} Spannweite | {{!}} Spannweite | ||
{{!}} Die Differenz aus dem Maximum und dem Minimum heißt Spannweite. | {{!}} Die Differenz aus dem Maximum und dem Minimum heißt Spannweite. | ||
{{! | {{!-}} | ||
{{!}} Zentralwert/Median | {{!}} Zentralwert/Median | ||
{{!}} Der Wert in der Mitte einer Rangliste heißt Median bzw. Zentralwert. | {{!}} Der Wert in der Mitte einer Rangliste heißt Median bzw. Zentralwert. | ||
{{! | {{!-}} | ||
{{!}} Quartil | |||
{{!}} Die Quartile teilen die Rangliste in vier Abschnitte. In jedem dieser Abschnitte befinden sich 25% der Werte. | |||
{{!-}} | |||
{{!}} unteres Quartil | {{!}} unteres Quartil | ||
{{!}} Der Wert | {{!}} Der Wert der Rangliste, der die untere Hälfte in zwei Hälften teilt, heißt unteres Quartil (also der Median der unteren Datenhälfte). | ||
{{! | {{!-}} | ||
{{!}} oberes Quartil | {{!}} oberes Quartil | ||
{{!}} Der Wert | {{!}} Der Wert der Rangliste, der die obere Hälfte in zwei Hälften teilt, heißt oberes Quartil (also der Median der oberen Datenhälfte). | ||
{{!)}}|3=Kurzinfo}} | {{!)}}|3=Kurzinfo}} | ||
Erstelle nun eine Rangliste der geworfenen Weiten und ermittle anhand dieser Rangliste die Kennwerte Minimum, | {{Box|Übung 2|Löse auf der Seite [https://mathe.aufgabenfuchs.de/wahrscheinlichkeit/relative-haeufigkeit.shtml '''Aufgabenfuchs'''] die nachfolgenden Aufgaben:<br> | ||
Bestimmung der Quartile: (Lies zunächst die Information vor Nr. 26.) | |||
* Nr. 26 und Nr. 27 | |||
|Üben}} | |||
Das Video erklärt dir, wie du die erhobenen Daten mit einem Boxplot darstellen kannst. Die Anzahl der Daten ist hier ungerade. | |||
{{#ev:youtube|IY_Q2vLYSis|800|center|||start=0&end=387}} | |||
Das nächste Video erklärt dies noch einmal, hier ist der Sonderfall, dass die Anzahl der Daten gerade ist. Die Bestimmung des Zentralwertes und der Quartile erfolgt hier leicht abgeändert: | |||
{{#ev:youtube|IY_Q2vLYSis|800|center|||start=387&end=605}} | |||
{{Box|Übung 3|Löse auf der Seite [https://mathe.aufgabenfuchs.de/wahrscheinlichkeit/relative-haeufigkeit.shtml '''Aufgabenfuchs'''] die nachfolgenden Aufgaben:<br> | |||
Boxplot: | |||
* Nr. 29 bis Nr. 32|Üben}} | |||
Erstelle nun eine Rangliste der geworfenen Weiten und ermittle anhand dieser Rangliste die Kennwerte Minimum, unteres Quartil, Median, oberes Quartil, Maximum. | |||
{{Fortsetzung|weiter=4) Daten darstellen (Boxplots)|weiterlink=Benutzer:Buss-Haskert/Daten/Daten darstellen}} | |||
Aktuelle Version vom 20. Oktober 2024, 15:30 Uhr
SEITE IM AUFBAU!
Wiederhole zunächst noch einmal die Begriffe: Urliste, Rangliste, Zentralwert (Median) und Mittelwert (Durchschnitt).
Nun noch einmal die obige Aufgabe:
Als Beispiel findest du hier die Werte von Tim und Tina.
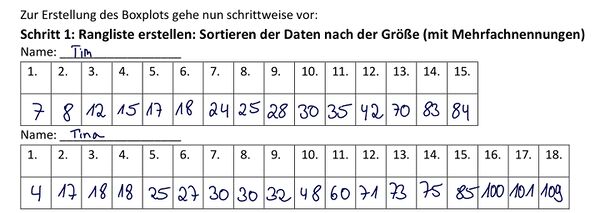
- schlechtester Sprung (Minimum): Tim 7 cm; Tina 4 cm
- bester Sprung (Maximum): Tim: 84 cm; Tina 109 cm
- Mittelwerte (arithmetisches Mittel):
Tim:
Tina:
- Median (Zentralwert):
Tim Rang: = 7,5, also Rang 8: 25 cm
Um diese Daten auszuwerten, helfen die dir schon bekannten Kennwerte:
Das Video erklärt dir, wie du die erhobenen Daten mit einem Boxplot darstellen kannst. Die Anzahl der Daten ist hier ungerade.
Das nächste Video erklärt dies noch einmal, hier ist der Sonderfall, dass die Anzahl der Daten gerade ist. Die Bestimmung des Zentralwertes und der Quartile erfolgt hier leicht abgeändert:
Erstelle nun eine Rangliste der geworfenen Weiten und ermittle anhand dieser Rangliste die Kennwerte Minimum, unteres Quartil, Median, oberes Quartil, Maximum.




