Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Modellieren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (2 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
<br> | <br> | ||
{{Navigation|[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme|0) Vorwissen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme|1) Lineare Gleichungen mit zwei Variablen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme|2) Lineare Gleichungssysteme]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen| 3) Lineare Gleichungssysteme zeichnerisch lösen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme rechnerisch lösen| 4) Lineare Gleichungssysteme rechnerisch lösen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Modellieren| 5) Modellieren]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Checkliste|6) Checkliste]]}} | {{Navigation|[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme|0) Vorwissen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme|1) Lineare Gleichungen mit zwei Variablen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme|2) Lineare Gleichungssysteme]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen| 3) Lineare Gleichungssysteme zeichnerisch lösen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme rechnerisch lösen| 4) Lineare Gleichungssysteme rechnerisch lösen]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Modellieren| 5) Modellieren]]<br>[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Checkliste|6) Checkliste]]}} | ||
{{Lösung versteckt|[[Datei:QR Code 9.1 Modellieren.jpg|rahmenlos|306x306px]]|QR Code anzeigen|Verbergen}} | |||
Es gibt verschiedene Bereiche, in denen lineare Gleichungssysteme (LGS) Anwendung finden: | Es gibt verschiedene Bereiche, in denen lineare Gleichungssysteme (LGS) Anwendung finden: | ||
[[Datei:Anwendungsbereiche Gleichungen.png|rahmenlos|800px]] | [[Datei:Anwendungsbereiche Gleichungen.png|rahmenlos|800px]] | ||
| Zeile 61: | Zeile 61: | ||
Anwendungsaufgaben lassen sich schrittweise lösen mithilfe eines Modells. Dabei wird die reale Situation (Sachsituation) in ein vereinfachtes mathematisches Modell übersetzt. Nun können wir diese Rechnung lösen. Die mathematische Lösung wird dann auf die Realität bezogen und die Ergebnisse werden zur Bewertung der Situation genutzt. | Anwendungsaufgaben lassen sich schrittweise lösen mithilfe eines Modells. Dabei wird die reale Situation (Sachsituation) in ein vereinfachtes mathematisches Modell übersetzt. Nun können wir diese Rechnung lösen. Die mathematische Lösung wird dann auf die Realität bezogen und die Ergebnisse werden zur Bewertung der Situation genutzt. | ||
Der nachfolgende Kreislauf veranschaulicht dies: | Der nachfolgende Kreislauf veranschaulicht dies:<br> | ||
[[Datei:Modellieren(1).jpg|rahmenlos|600x600px]] | [[Datei:Modellieren(1).jpg|rahmenlos|600x600px]] | ||
{{Box|Beispielaufgabe Klassenfahrt|Die Jahrgangsstufe 9 fährt mit insgesamt 110 Schülerinnen und Schülern auf Klassenfahrt. In der Jugendherberge gibt es insgesamt 28 Zimmer. Die Mädchen erhalten die Dreibettzimmer, die Jungen die Fünfbettzimmer.|Üben}} | {{Box|Beispielaufgabe Klassenfahrt|Die Jahrgangsstufe 9 fährt mit insgesamt 110 Schülerinnen und Schülern auf Klassenfahrt. In der Jugendherberge gibt es insgesamt 28 Zimmer. Die Mädchen erhalten die Dreibettzimmer, die Jungen die Fünfbettzimmer.|Üben}} | ||
| Zeile 84: | Zeile 84: | ||
-2x = -30 |:(-2)<br> | -2x = -30 |:(-2)<br> | ||
x = <span style="color:red">15</span> | x = <span style="color:red">15</span> | ||
Bestimme nun y, indem du x =<span style="color:red"> 15</span> in I. (oder II.) einsetzt:<br> | Bestimme nun y, indem du x =<span style="color:red"> 15</span> in I. (oder II.) einsetzt:<br> | ||
I. <span style="color:red">15</span> + y = 28 |-15<br> | I. <span style="color:red">15</span> + y = 28 |-15<br> | ||
Aktuelle Version vom 15. August 2024, 08:53 Uhr
1) Lineare Gleichungen mit zwei Variablen
2) Lineare Gleichungssysteme
3) Lineare Gleichungssysteme zeichnerisch lösen
4) Lineare Gleichungssysteme rechnerisch lösen
5) Modellieren
6) Checkliste
Es gibt verschiedene Bereiche, in denen lineare Gleichungssysteme (LGS) Anwendung finden:
Bist du fit? Vorübungen
Addition: 1. Summand + 2. Summand = Wert derSumme
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Multiplikation: 1. Faktor ∙ 2. Faktor = Wert des Produktes
Division: Dividend: Divisor = Wert des Quotienten
| Addition | addieren | vermehren | plus | |
| Subtraktion | subtrahieren | vermindern | minus | |
| Multiplikation | multiplizieren | verdoppeln | vervielfachen | mal |
| Division | dividieren | halbieren | teilen | geteilt |
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme.
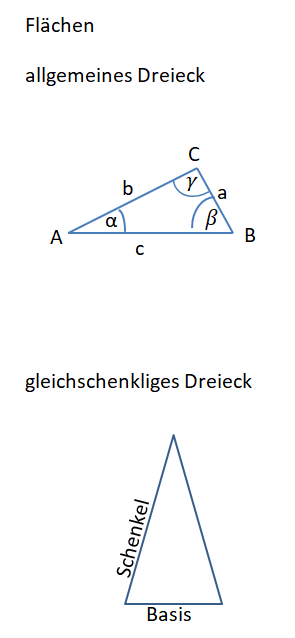
| Quadrat | u = 4·a | A = a² | ||
| Rechteck | u = 2a + 2b | A = a·b | ||
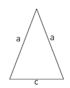
| gleichschenkliges Dreieck | u = 2a + c | 2 gleich lange Seiten | α+β+γ=180° | |
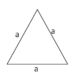
| gleichseitiges Dreieck | u = 3a | 3 gleich lange Seiten | α+β+γ=180° |
5) Modellieren mit linearen Gleichungssystemen
Anwendungsaufgaben lassen sich schrittweise lösen mithilfe eines Modells. Dabei wird die reale Situation (Sachsituation) in ein vereinfachtes mathematisches Modell übersetzt. Nun können wir diese Rechnung lösen. Die mathematische Lösung wird dann auf die Realität bezogen und die Ergebnisse werden zur Bewertung der Situation genutzt.
Der nachfolgende Kreislauf veranschaulicht dies:
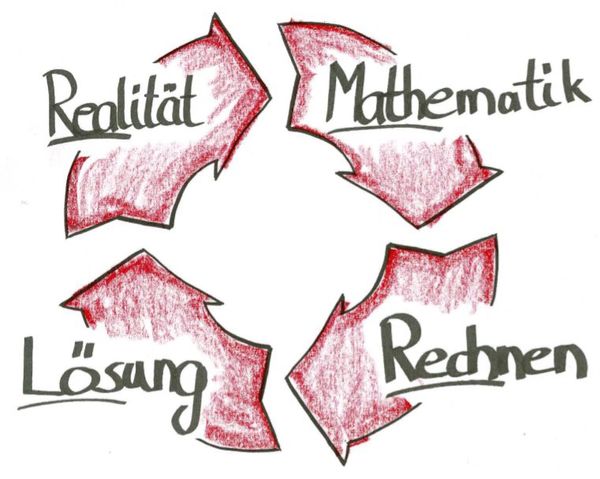
1. Realität: 110 Schülerinnen und Schüler insgesamt, verteilen auf 28 Zimmer, wobei es Dreibett- und Fünfbettzimmer gibt.
2. Mathematik: Lege die Bedeutung der Variablen fest und stelle ein lineares Gleichungssystem mit zwei Gleichungen auf.Bedeutung der Variablen:
x = Anzahl der Dreibettzimmer, y = Anzahl der Fünfbettzimmer
lineare Gleichungen:
I. x + y = 28
II. 3x + 5y = 110
3. Rechnen: Löse dieses Gleichungssystem mit einem geeigneten Verfahren .Löse mit dem Gleichsetzungsverfahren:
I. x + y = 28 |-x
II. 3x + 5y = 110 |-3x
I. y = -x + 28 |∙5
II. 5y = -3x + 110
I. 5y = -5x + 140
II. 5y = -3x + 110
I. = II.
-5x + 140 = -3x + 110 |+3x
-2x + 140 = 110 |-140
-2x = -30 |:(-2)
x = 15
Bestimme nun y, indem du x = 15 in I. (oder II.) einsetzt:
I. 15 + y = 28 |-15
y = 13
Probe:
x = 15 und y = 13 in I. und II. einsetzen:
I. 15 + 13 = 28 II. 3∙15 + 5∙13 = 110
28 = 28 (w) 110 = 110 (w)
4. Lösung: (15|13)
Es gibt 15 Dreibettzimmer und 13 Fünfbettzimmer in der Jugendherberge.
x = erste Zahl; y=zweite Zahl
Bedeutung der Variablen: Es gibt die Basis und die Schenkel des Dreiecks. Also könntest du x=Länge der Basis und y=Länge eines Schenkels festlegen.
x=Länge der Basis; y=Länge eines Schenkels
I. x+2y = 35 "Der Umfang beträgt 35cm. (Laufe um das Dreieck herum.)"
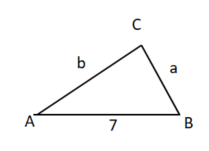
I.a + b = 12 ("zusammen sind sie 12 cm lang")
II. b = a + 5 ("eine davon ist 5 cm länger als die andere")
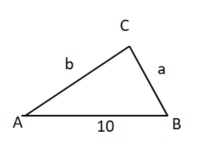
I.7 + a + b = 18 ("Der Umfang beträgt 18 cm")
II. b = a + 1 ("Die Seitenlängen unterscheiden sich um 1")
x=Anzahl der Dreiergruppen ; y=Anzahl der Vierergruppen
Eine Dreiergruppe mit Mädchen bedeutet dann insgesamt 3∙x Mädchen und eine Vierergruppe mit Jungen entsprechend 4∙y Jungen.
x=Anzahl der Dreierbettzimmer; y=Anzahl der Fünfbettzimmer
Ein Dreibettzimmer fasst 3∙x Personen und ein Fünfbettzimmer entsprechend 5∙y.
Bedeutung der Variablen: x=Preis pro Erwachsener; y=Preis pro Kind
I. 2x + 2y = 28
II. x + 3y = 22
Bedeutung der Variablen: x=Geschwindigkeit des Bootes in km/h; y=Fließgeschwindigkeit des Flusses in km/h
I. 2x + 2y = 48 (Das Boot fährt in 2 Stunden mit der Geschwindigkeit des Bootes und des Flusses 48 km)
II. 3x - 3y = 48 (Das Boot fährt in 3 Stunden mit der Geschwindigkeit des Bootes verringert um die Geschwindigkeit des Flusses, da der Fluss ja nun stromaufwärts gefahren wird.)
Bedeutung der Variablen: x=Geschwindigkeit des Radfahrers in km/h; y=Geschwindigkeit des Autos in km/h
I. 3x - 12 = x (Der Radfahrer fährt 3 Stunden, das Auto 1 Stunde und der Weg des Radfahrers beträgt 12 km mehr als der des Autos)
II. 4x + 20 = 2x (Der Radfahrer fährt 4 Stunden lang, das Auto 2 Stunden. Der Weg des Radfahrers ist 20 km weniger als der des Autos.)
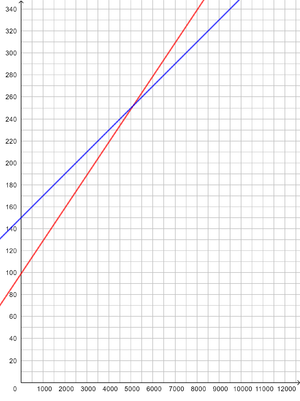
Realität Die Kosten setzen sich zusammen aus den Anschaffungskosten und den Kosten für die Druckerpatronen (pro 1000 Blatt).
2. Mathematik: Die Variablen haben also die Bedeutung x=Anzahl der ausgedruckten Seiten (in Tausend) und y=Kosten insgesamt.