Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel/1) Kreis: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (54 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
{{Navigation| | |||
[[Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel/1) Kreis|1) Kreis]]<br> | |||
[[Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel/2) Kreisausschnitt|2) Kreisausschnitt*]]<br> | |||
[[Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel/2) Winkel|3) Winkel]]<br> | |||
}} | |||
==1. Kreis== | ==1. Kreis== | ||
[[Datei: Wallpaper-2574943 1920.png|300px]] | [[Datei: Wallpaper-2574943 1920.png|300px]] | ||
| Zeile 5: | Zeile 13: | ||
{{Box|Idee|Schaue dich in deiner Umgebung um. Welche kreisförmigen Gegenstände findest du? Notiere.|Unterrichtsidee }} | {{Box|Idee|Schaue dich in deiner Umgebung um. Welche kreisförmigen Gegenstände findest du? Notiere.|Unterrichtsidee }} | ||
{{Box|Übung | <ggb_applet id="tsxwncze" width="600" height="600" border="888888" /> | ||
<small>Applet: FLINK-Team</small> | |||
{{Box|Übung 1: Kreise erkennen|Bearbeite die folgende LearningApp.|Üben}} | |||
{{LearningApp|app=pcje1vqgc21 |width=100%|height=500px}} | {{LearningApp|app=pcje1vqgc21 |width=100%|height=500px}} | ||
{{Box|Übung | {{Box|Übung 2: Aufgaben im Buch|Bearbeite die folgende Aufgabe im Heft. <br> | ||
* S. 11, Nr. 4a |Üben}} | * S. 11, Nr. 4a |Üben}} | ||
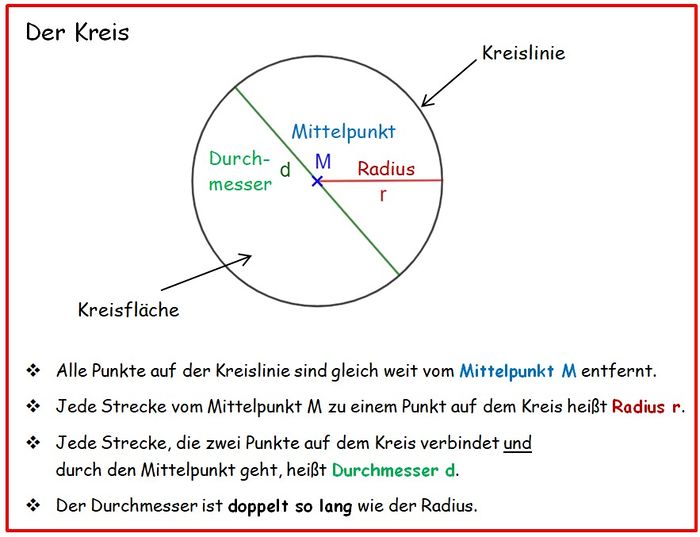
===1.2 Fachbegriffe im Kreis=== | ===1.2 Fachbegriffe im Kreis=== | ||
<ggb_applet id="ujk9auzs" width="750" height="448" border="888888" /> | |||
<small>Applet: FLINK-Team</small> | |||
{{Box|Merke: Der Kreis| | {{Box|Merke: Der Kreis| | ||
| Zeile 18: | Zeile 31: | ||
{{Box|Übung | {{Box|Übung 3: Fachbegriffe im Kreis|Bearbeite die folgenden LearningApps und das GeoGebra-Quiz.|Üben}} | ||
{{LearningApp|app=puginrvgk21 |width=100%|height=500px}} | {{LearningApp|app=puginrvgk21 |width=100%|height=500px}} | ||
{{LearningApp|app=pijgzv8t521 |width=100%|height=500px}} | {{LearningApp|app=pijgzv8t521 |width=100%|height=500px}} | ||
<ggb_applet id="yh75ppx6" width="750" height="450" border="888888" /> | |||
<small>Applet: FLINK-Team</small> | |||
{{Box|Übung | {{Box|Übung 4: Radius und Durchmesser bestimmen und berechnen|Bearbeite die folgende Online-Übung.|Üben}} | ||
{{h5p-zum|id=15985|height=800px}} | {{h5p-zum|id=15985|height=800px}} | ||
| Zeile 28: | Zeile 44: | ||
===1.3 Kreise zeichnen=== | ===1.3 Kreise zeichnen=== | ||
{{Box|Erklärvideo | {{Box|Erklärvideo 1|Schau dir das Video zu ''Kreis mithilfe des Zirkels zeichnen'' an.|Kurzinfo}} | ||
{{#ev:youtube|qcaj6sxGD78|800|center}} | {{#ev:youtube|qcaj6sxGD78|800|center}} | ||
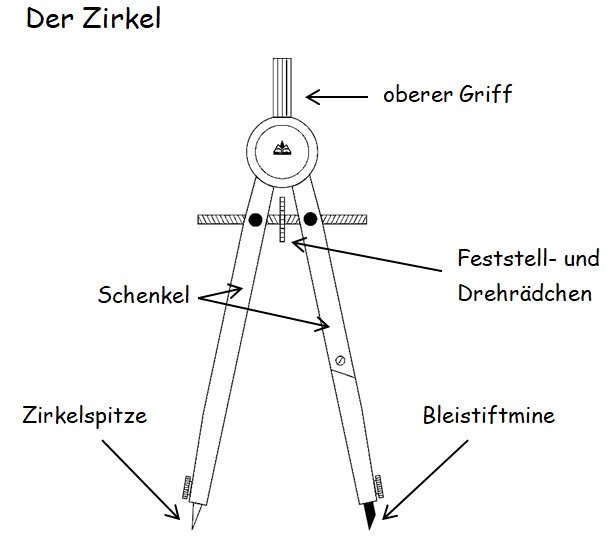
{{Box|Info| | {{Box|Info 1| | ||
[[Datei:Der Zirkel.jpg|700px]]|Kurzinfo}} | [[Datei:Der Zirkel.jpg|700px]]|Kurzinfo}} | ||
| Zeile 38: | Zeile 54: | ||
{{Box|Übung | {{Box|Übung 5: Kreis mit dem Zirkel zeichnen|Bearbeite die folgende LearningApp.|Üben}} | ||
{{LearningApp|app=pye3jraqn21 |width=100%|height=700px}} | {{LearningApp|app=pye3jraqn21 |width=100%|height=700px}} | ||
{{Box|Übung | {{Box|Übung 6: Aufgaben im Buch|Bearbeite die folgenden Aufgaben im Heft. <br> | ||
* S. 11, Nr. 2 | * '''S. 11, Nr. 2''' | ||
* S. 11, Nr. 3 | * '''S. 11, Nr. 3''' <br> Wähle für die Aufgabenteile '''a)''' und '''b)''' als Einheit 1 cm und wähle für den Aufgabenteil '''c)''' als Einheit 1 Kästchen. | ||
* S. 11, Nr. 5 | * '''S. 11, Nr. 5''' | ||
* S. 11, Nr. 6 |Üben}} | * '''S. 11, Nr.7''' Nutze das Applet (GeoGebra) unten. | ||
* '''S. 11, Nr. 6''' [Zusatzaufgabe]|Üben}} | |||
| Zeile 53: | Zeile 70: | ||
* Wandle dm zunächst in cm oder mm um. Denke an die Umrechnungszahl bei Längeneinheiten. | * Wandle dm zunächst in cm oder mm um. Denke an die Umrechnungszahl bei Längeneinheiten. | ||
|2=Tipp zu Nr. 2|3=Tipp ausblenden}} | |2=Tipp zu Nr. 2|3=Tipp ausblenden}} | ||
<br> | <br> | ||
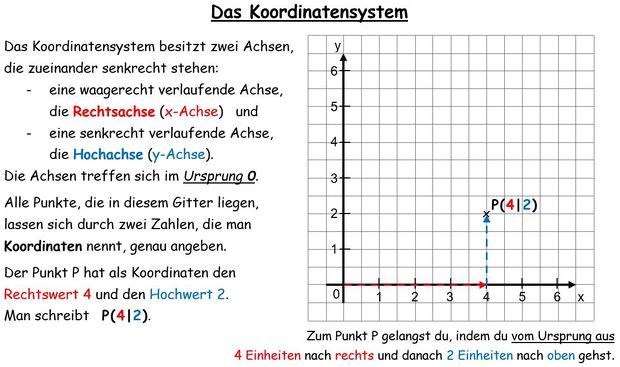
{{Lösung versteckt|1=[[Datei:Koordinatensystem Merke.jpg|620 px|center|Koordinatensystem_Erinnerung]]|2=Tipp zu Nr. 3 - Wie war das nochmal mit dem Koordinatensystem (= Quadratgitter)?|3=Tipp ausblenden}} | {{Lösung versteckt|1=[[Datei:Koordinatensystem Merke.jpg|620 px|center|Koordinatensystem_Erinnerung]]|2=Tipp zu Nr. 3 - Wie war das nochmal mit dem Koordinatensystem (= Quadratgitter)?|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
* zu a und b) Zeichne zunächst den Mittelpunkt ein und stelle dann den gewünschten Radius bzw. Durchmesser ein. <br> | * zu a und b) Zeichne zunächst den Mittelpunkt ein und stelle dann den gewünschten Radius bzw. Durchmesser ein. <br> | ||
* zu c) Zeichne die Punkte M und P ein. Denke daran, dass M der Mittelpunkt ist. Die Verbindung zwischen M und P ist die Länge des Radius. | * zu c) Zeichne die Punkte M und P ein. Denke daran, dass M der Mittelpunkt ist. Die Verbindung zwischen M und P ist die Länge des Radius. <br> | ||
|2=Tipp zu Nr. 3|3=Tipp ausblenden}} | |2=Tipp zu Nr. 3|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1= <span style="color:red">noch | {{Lösung versteckt|1= <u>KONTROLLE</u>: Überprüfe jeweils, ob der angegebene Punkt auf der Kreislinie des von dir gezeichneten Kreises liegt. <br> | ||
<span style="color:green">Wenn JA, hast du alles richtig gemacht.</span> <br> | |||
<span style="color:red">Wenn NEIN, musst du die Aufgabe berichtigen (= noch einmal neu bearbeiten).</span> <br> | |||
'''a)''' P(6/8) <br> | |||
'''b)''' P(7/12) <br> | |||
'''a)''' Q(2/10) <br> | |||
|2=Lösung zu Nr. 3|3=Lösung ausblenden}} | |2=Lösung zu Nr. 3|3=Lösung ausblenden}} | ||
{{Lösung versteckt|1=<ggb_applet id="qvk5edd4" width="1048" height="570" border="888888" />|2=Lösung zu Nr. 3 (Applet GeoGebra)|3=Lösung ausblenden}} | |||
<br> | <br> | ||
{{Lösung versteckt|1= < | {{Lösung versteckt|1=Prüfapplet: Verschiebe die Mittelpunkte der Kreise so, dass die Bedingungen aus der Aufgabe erfüllt sind.<br> | ||
<ggb_applet id="zcma8hrd" width="770" height="627" border="888888" /><br> | |||
<small>Applet von C. Buß-Haskert</small> | |||
allgemein: Wie können zwei Kreise zueinander liegen?<br> | |||
<ggb_applet id="ymfjpsnm" width="750" height="669" border="888888" /> | |||
<small>Applet des FLINK-Teams</small>|2=Tipp zu Nr. 5 (Prüfapplets)|3=Tipp ausblenden}} | |||
{{Lösung versteckt|1= | |||
'''a)''' Zwei Kreise berühren sich nicht, wenn die Entfernung ihrer Mittelpunkte größer ist als die Summe ihrer Radien. <br> | |||
'''b)''' Zwei Kreise schneiden sich, wenn die Entfernung ihrer Mittelpunkte kleiner ist als die Summe ihrer Radien. <br> | |||
'''c)''' Zwei Kreise berühren sich, wenn die Entfernung ihrer Mittelpunkte der Summe ihrer Radien entspricht. | |||
|2=Tipp zu Nr. 5|3=Tipp ausblenden}} | |2=Tipp zu Nr. 5|3=Tipp ausblenden}} | ||
{{Lösung versteckt|1= < | |||
|2= | |||
{{Lösung versteckt|1=Applet zu Nr. 7<br> | |||
<ggb_applet id="ckcmwnbd" width="842" height="771" border="888888" /> | |||
<small>Applet von C.Buß-Haskert</small><br>|2=Applet zu Nr. 7 (GeoGebra)|3=Lösung ausblenden}} | |||
{{Lösung versteckt|1=Applet zu Nr. 7d:<br> | |||
<ggb_applet id="caw5zg8w" width="842" height="771" border="888888" />|2=Tipp zu Nr. 7d|3=Lösung ausblenden}} | |||
{{Box|1=Nur für Profis: Kreise und Quadrate|2=Gegeben ist ein Kreis mit dem Radius r=3cm. Zeichne diesen Kreis in dein Heft. Zeichne anschießend ein Quadrat so ein, dass seine vier Eckpunkte auf der Kreislinie liegen.|3=Üben}} | |||
{{Lösung versteckt|Denke daran, den Mittelpunkt des Kreises zu markieren! Die Diagonalen des Quadrates gehen durch den Mittelpunkt. Außerdem stehen sie senkrecht zueinander. So kannst du die vier Eckpunkte mithilfe der Diagonalen finden.|Tipp|Tipp ausblenden}} | |||
{{Box|Kreise zeichnen mit GeoGebra|Bearbeite die nachfolgenden GeoGebra-Applets. Hier lernst du die verschiedenen Möglichkeiten, wie du mit GeoGebra Kreise zeichnen kannst.|Üben}} | |||
<ggb_applet id="pabffkwv" width="760" height="450" border="888888" /> | |||
<small>Applet des FLINK Teams</small> Originallink: https://www.geogebra.org/m/znkjp5ad | |||
<ggb_applet id="hubddm9f" width="760" height="450" border="888888" /> | |||
<small>Applet des FLINK Teams</small> Originallink: https://www.geogebra.org/m/sr2xpnfv | |||
<ggb_applet id="wpdy7vq6" width="700" height="500" border="888888" /> | |||
<small>Applet des FLINK Teams</small> Originallink: https://www.geogebra.org/m/dxnsxffb | |||
<br> | <br> | ||
===1.4 Muster mit Zirkel zeichnen und ergänzen=== | ===1.4 Muster mit Zirkel zeichnen und ergänzen=== | ||
[[Datei:Compass-4363135 1920.png|500px]] | [[Datei:Compass-4363135 1920.png|500px]] | ||
{{Box|Übung | {{Box|Übung 7: Aufgaben im Buch|Bearbeite die folgenden Aufgaben im Heft. <br> | ||
* S. 11, Nr. 8 | * S. 11, Nr. 8 | ||
* S. 11, Nr. 9 | * S. 11, Nr. 9 | ||
* S. 11, Nr. 10 [Zusatzaufgabe] |Üben}} | * S. 11, Nr. 10 [Zusatzaufgabe] |Üben}} | ||
Für Schnellrechner:<br> | |||
Vervollständige die Kreismuster mit dem Programm GeoGebra.<br> | |||
<ggb_applet id="aWbFN55G" width="789" height="500" border="888888" /> | |||
<small>Applet von Maria Huber</small> | |||
<br> | |||
{{Fortsetzung|weiter=2) Kreisausschnitt*|weiterlink=Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel/2) Kreisausschnitt|vorher= zurück zum Vorwissen|vorherlink=Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel}} | |||
{{Fortsetzung|weiter= | {{Fortsetzung|weiter=3) Winkel|weiterlink=Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel/2) Winkel|vorher= zurück zum Vorwissen|vorherlink=Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel}} | ||
Aktuelle Version vom 30. Juli 2024, 12:55 Uhr
1. Kreis
1.1 Kreise erkennen

Applet: FLINK-Team
1.2 Fachbegriffe im Kreis

Applet: FLINK-Team

Applet: FLINK-Team
1.3 Kreise zeichnen
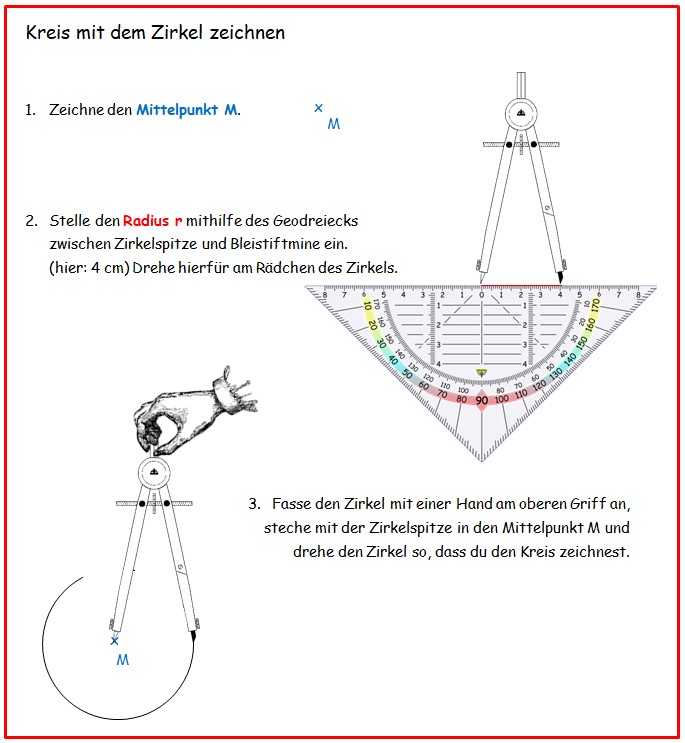
ACHTUNG: Achte darauf, ob der Radius oder der Durchmesser angegeben ist!
- Stelle den Radius mithilfe des Geodreiecks ein, indem du den entsprechenden Abstand zwischen Zirkelspitze und Bleistiftmine einstellst.
- Wandle dm zunächst in cm oder mm um. Denke an die Umrechnungszahl bei Längeneinheiten.
- zu a und b) Zeichne zunächst den Mittelpunkt ein und stelle dann den gewünschten Radius bzw. Durchmesser ein.
- zu c) Zeichne die Punkte M und P ein. Denke daran, dass M der Mittelpunkt ist. Die Verbindung zwischen M und P ist die Länge des Radius.
KONTROLLE: Überprüfe jeweils, ob der angegebene Punkt auf der Kreislinie des von dir gezeichneten Kreises liegt.
Wenn JA, hast du alles richtig gemacht.
Wenn NEIN, musst du die Aufgabe berichtigen (= noch einmal neu bearbeiten).
a) P(6/8)
b) P(7/12)

Prüfapplet: Verschiebe die Mittelpunkte der Kreise so, dass die Bedingungen aus der Aufgabe erfüllt sind.

Applet von C. Buß-Haskert
allgemein: Wie können zwei Kreise zueinander liegen?

a) Zwei Kreise berühren sich nicht, wenn die Entfernung ihrer Mittelpunkte größer ist als die Summe ihrer Radien.
b) Zwei Kreise schneiden sich, wenn die Entfernung ihrer Mittelpunkte kleiner ist als die Summe ihrer Radien.
Applet zu Nr. 7

Applet zu Nr. 7d:


Applet des FLINK Teams Originallink: https://www.geogebra.org/m/znkjp5ad

Applet des FLINK Teams Originallink: https://www.geogebra.org/m/sr2xpnfv

Applet des FLINK Teams Originallink: https://www.geogebra.org/m/dxnsxffb
1.4 Muster mit Zirkel zeichnen und ergänzen
Für Schnellrechner:
Vervollständige die Kreismuster mit dem Programm GeoGebra.

Applet von Maria Huber