Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo: Unterschied zwischen den Versionen
Markierung: Quelltext-Bearbeitung 2017 |
|||
| (44 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 14: | Zeile 14: | ||
Deshalb können in der Realität nur Abschnitte von natürlichen Vorgängen (beispielsweise das Wachstum von Pflanzen) näherungsweise durch das lineares Wachstum beschrieben werden. Technische Vorgänge (beispielsweise der Füllstand einer Badewanne) werden ebenfalls durch lineares Wachstum beschrieben werden, jedoch gibt es hier meist eine Begrenzung (z.B. bedingt durch das Fassungsvermögen der Badewanne).<ref>Ableitinger, C., "Biomathematische Modelle im Unterricht - Fachwissenschaftliche und didaktische Grundlagen und Unterrichtsmaterialien", 1. Auflage 2010, S.32 ff. (2.1.1 Lineares Wachstum)</ref> | Deshalb können in der Realität nur Abschnitte von natürlichen Vorgängen (beispielsweise das Wachstum von Pflanzen) näherungsweise durch das lineares Wachstum beschrieben werden. Technische Vorgänge (beispielsweise der Füllstand einer Badewanne) werden ebenfalls durch lineares Wachstum beschrieben werden, jedoch gibt es hier meist eine Begrenzung (z.B. bedingt durch das Fassungsvermögen der Badewanne).<ref>Ableitinger, C., "Biomathematische Modelle im Unterricht - Fachwissenschaftliche und didaktische Grundlagen und Unterrichtsmaterialien", 1. Auflage 2010, S.32 ff. (2.1.1 Lineares Wachstum)</ref> | ||
[[Gymnasium Marktbreit/Wissenschaftswoche 2024/Beispiele Lineares Wachstum|Beispielaufgabe lineares Wachstum]] | [[Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo/Beispiele Lineares Wachstum|Beispielaufgabe lineares Wachstum]] | ||
[[Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo/Experiment Lineares Wachstum|Experiment lineares Wachstum]] | |||
[[Datei:Lineares Wachstum 1.png|zentriert|mini|Lineares Wachstum]] | [[Datei:Lineares Wachstum 1.png|zentriert|mini|Lineares Wachstum]] | ||
| Zeile 22: | Zeile 24: | ||
'''Beispiele''': Bakterienwachstum, Wachstum durch Zellteilung, Bevölkerungswachstum, Ausbreitung von Pandemien, Abkühlungen | '''Beispiele''': Bakterienwachstum, Wachstum durch Zellteilung, Bevölkerungswachstum, Ausbreitung von Pandemien, Abkühlungen | ||
Die ''' | Die '''Rekursionsgleichung''' lautet: <math>N_{t+1}=N_t\cdot(1+p)</math> | ||
mit <math>q=(1+p)</math> als Wachstumsfaktor <math>q=\frac{neuer Wert}{alter Wert}</math> | mit <math>q=(1+p)</math> als Wachstumsfaktor <math>q=\frac{neuer Wert}{alter Wert}</math> | ||
und <math>p</math> als Wachstumsrate, <math>p</math>%<math>=\frac{neue Größe - alte Größe}{alte Größe}</math> | und <math>p</math> als Wachstumsrate, <math>p</math>%<math>=\frac{neue Größe - alte Größe}{alte Größe}</math>, | ||
'''Lösung der Gleichung''': <math>N_t=N_0\cdot q^t</math> | |||
Die Lösungsgleichung ergibt sich aus der ursprünglichen Gleichung. | |||
wobei <math>N_0</math> der Bestand zum Zeitpunkt <math>0</math> ist und <math>N_t</math> der Bestand <math>N</math> zum Zeitpunkt <math>t</math><ref>Ableitinger, C., "Biomathematische Modelle im Unterricht - Fachwissenschaftliche und didaktische Grundlagen und Unterrichtsmaterialien", 1. Auflage 2010, S.32 ff. (2.1.2 Exponentielles Wachstum)</ref> | |||
[[Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo/Beispiele Exponentielles Wachstum|Beispielaufgabe Exponentielles Wachstum]] | [[Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo/Beispiele Exponentielles Wachstum|Beispielaufgabe Exponentielles Wachstum]] | ||
[[Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo/Experiment Exponentielles Wachstum|Experiment Exponentielles Wachstum]] | |||
[[Datei:Screenshot 2024-07-04 090749.png|mini|Exponentielles Wachstum|zentriert]] | [[Datei:Screenshot 2024-07-04 090749.png|mini|Exponentielles Wachstum|zentriert]] | ||
=== | === Logistisches Wachstum === | ||
Logistische Modelle beschreiben Wachstumsprozesse in der Biologie und der Demographie. | Logistische Modelle beschreiben Wachstumsprozesse in der Biologie und der Demographie. | ||
Dadurch werden reale Wachstumsprozesse modelliert, beispielsweise als Basismodell für Bevölkerungs- und Pflanzenwachstum, als Abstatz für ein neues Produkt oder als Anzahl für Krankheiten immunisierter Personen. | Dadurch werden reale Wachstumsprozesse modelliert, beispielsweise als Basismodell für Bevölkerungs- und Pflanzenwachstum, als Abstatz für ein neues Produkt oder als Anzahl für Krankheiten immunisierter Personen. | ||
Francois Verhulst hat dieses Modell als erster benutzt, um die Bevölkerungsentwicklung zu beschreiben. Allerdings ist dies nur möglich gewesen, da der Belgier Benjamin Gompertz (1825) Vorarbeiten geleistet hatte. | Francois Verhulst<ref>https://de.wikipedia.org/wiki/Pierre-Fran%C3%A7ois_Verhulst</ref> hat dieses Modell als erster benutzt, um die Bevölkerungsentwicklung zu beschreiben. Allerdings ist dies nur möglich gewesen, da der Belgier Benjamin Gompertz (1825) Vorarbeiten geleistet hatte. | ||
Zu Beginn verläuft der Graph der Funktion meist exponentiell, im weiteren Verlauf flacht er dann ab, sodass die typisch s-förmige Funktion entsteht. | Zu Beginn verläuft der Graph der Funktion meist exponentiell, im weiteren Verlauf flacht er dann ab, sodass die typisch s-förmige Funktion entsteht. | ||
Die '''Differenzialgleichung''' lautet: <math>N'(t)=a\cdot N(t)\cdot (K-N(t))</math> | Die '''Differenzialgleichung''' lautet: <math>N'(t)=a\cdot N(t)\cdot (K-N(t))</math> | ||
| Zeile 50: | Zeile 56: | ||
<math>N(t)</math> die Größe zum Zeitpunkt t, <math>N_0</math> Größe zu Beginn des Beobachtungszeitraums, <math>a</math> Konstante<ref>Ableitinger, C., "mathematiklehren - Erfolgreich unterrichten: Konzepte und Materialien", S.31 ff. (Ein Schritt nach dem anderen - Diskretisieren als Zugang zum logistischen Modell)</ref> | <math>N(t)</math> die Größe zum Zeitpunkt t, <math>N_0</math> Größe zu Beginn des Beobachtungszeitraums, <math>a</math> Konstante<ref>Ableitinger, C., "mathematiklehren - Erfolgreich unterrichten: Konzepte und Materialien", S.31 ff. (Ein Schritt nach dem anderen - Diskretisieren als Zugang zum logistischen Modell)</ref> | ||
zum Lösen von Problemen wird meist die '''Regressionsgleichung''' verwendet:<ref>Ableitinger, C., "Biomathematische Modelle im Unterricht - Fachwissenschaftliche und didaktische Grundlagen und Unterrichtsmaterialien", 1. Auflage 2010, S.43 ff. (2.1.4 Logistische Modelle)</ref> | |||
<math>N(x)={K \over N_0 + (K-N_0\cdot e^{-K\cdot k \cdot x}) }</math> | |||
[[Gymnasium Marktbreit/Wissenschaftswoche 2024/11bMatheInfo/Beispiele Logistisches Wachstum|Beispielaufgabe logistisches Wachstum]] | |||
[[Datei:Screenshot 2024-07-04 091416.png|mini|logistisches Wachstum|zentriert]] | |||
===Einsatz von Algorithmen und KI um Vorhersagen zu treffen=== | ===Einsatz von Algorithmen und KI um Vorhersagen zu treffen=== | ||
Heute werden viele alltägliche Vorhersagen, wie z.B. das Wetter, durch Algorithmen und Big Data (Verwendung von großen Datenmengen) und teilweise sogar mithilfe von KI (Künstliche Intelligenz) von Computer berechnet. Es gibt aber auch weniger bekannte und deutlich komplexere Anwendungszwecke, die große Auswirkungen auf die Gesellschaft haben können: | Heute werden viele alltägliche Vorhersagen, wie z.B. das Wetter, durch Algorithmen und Big Data (Verwendung von großen Datenmengen) und teilweise sogar mithilfe von KI (Künstliche Intelligenz) von Computer berechnet. Es gibt aber auch weniger bekannte und deutlich komplexere Anwendungszwecke, die große Auswirkungen auf die Gesellschaft haben können: | ||
Google entwickelte beispielsweise Google Flu Trends, ein Service, der Grippewellen vorhersagen sollte. Jedoch waren die Vorhersagen, trotz erster Erfolge, meist unzuverlässig. Aus diesem Beispiel lässt sich gut ableiten, was bei der Verwendung von Algorithmen für Vorhersagen unbedingt beachtet werden muss. Um eine genaue Vorhersage treffen zu können, müssen Parameter ständig angepasst werden, da sich die Umstände in der Realität ständig verändern. Außerdem muss auf die Qualität der Daten geachtet werden. | Google entwickelte beispielsweise Google Flu Trends<ref>https://en.wikipedia.org/wiki/Google_Flu_Trends</ref>, ein Service, der Grippewellen vorhersagen sollte. Jedoch waren die Vorhersagen, trotz erster Erfolge, meist unzuverlässig. Aus diesem Beispiel lässt sich gut ableiten, was bei der Verwendung von Algorithmen für Vorhersagen unbedingt beachtet werden muss. Um eine genaue Vorhersage treffen zu können, müssen Parameter ständig angepasst werden, da sich die Umstände in der Realität ständig verändern. Außerdem muss auf die Qualität der Daten geachtet werden.<ref>Drösser, C., "Total berechenbar? Wenn Algorithmen für uns entscheiden", 2016, S.129 ff. (6. Vorhersagen - Wie aus Korrelationen Prognosen werden)</ref> | ||
Auch gibt es bereits seit Jahren den Versuch KI und Algorithmen einzusetzen, | Auch gibt es bereits seit Jahren den Versuch KI und Algorithmen einzusetzen, um Verbrechen vorherzusagen uns somit präventiv zu verhindern, oder Person per Kontrollen auszuwählen. Der | ||
Film "Minority Report" (2002)<ref>https://de.wikipedia.org/wiki/Minority_Report</ref>, beschäftigte sich mit Ansätzen teilen mit dieser Idee, aber insbesondere mit den Gefahren und Risiken, als auch den sozialen Aspekten. Hauptkrikpunkt ist der soziale Aspekt der fairen Behandlung, da Vorhersagen, deren Grundlage rein aus bestehenden Daten bestehen, nie absolut dem entsprechen, was passieren wird und so unschuldige Menschen bestraft werden könnten. Besonders angreifbar in dieser Hinsicht ist der Einsatz von KI, die ihre Parameter selbst festlegt, da hier nicht einsehbar ist, was diese Parameter besagen. Aufgrund dieser fehlenden Möglichkeit der Überwachung, kann es zu fatalen Fehlentscheidungen (z.B. bei Parametern, die auf Falschinformationen beruhen) oder Diskriminierung(Wohnort und Hautfarbe, könnten fälschlicherweise auch als Parameter genutzt werden) kommen<ref>Drösser, C., "Total berechenbar? Wenn Algorithmen für uns entscheiden", 2016, S.118 ff. (6. Vorhersagen - Wie aus Korrelationen Prognosen werden)</ref>. | |||
===Blick in die Zukunft=== | ===Blick in die Zukunft=== | ||
Mit Hilfe der genannten Möglichkeiten sollen aber nicht nur Vorhersagen für kurze, sondern auch für lange Zeitintervalle getroffen werden, um besser auf medizinische, demographische und technologische Ereignisse vorbereitet zu sein. Für die zuverlässige Umsetzung und Nutzung müssen bestehende Programme und Algorithmen jedoch ständig weiterentwickelt, ergänzt und überarbeitet werden.<ref>Drösser, C., "Total berechenbar? Wenn Algorithmen für uns entscheiden", 2016, S.117 ff. (6. Vorhersagen - Wie aus Korrelationen Prognosen werden)</ref> | Mit Hilfe der genannten Möglichkeiten sollen aber nicht nur Vorhersagen für kurze, sondern auch für lange Zeitintervalle getroffen werden, um besser auf medizinische, demographische und technologische Ereignisse vorbereitet zu sein. So sind einige positive Beispiele Ausweichempfehlungen bei Stau, neue Fertigungsmethoden in der Produktion oder aber die Nutzung von Smarthome-Systemen. Jedoch gibt es auch negative Aspekte für die KI-Nutzung in der Zukunft, beispielsweise ist eine Abhängigkeit und somit Abgrenzung von realen Menschen, durch eine realistischere Umsetzung verschiedener Programme, möglich. Für die zuverlässige Umsetzung und Nutzung müssen bestehende Programme und Algorithmen jedoch ständig weiterentwickelt, ergänzt und überarbeitet werden.<ref>Drösser, C., "Total berechenbar? Wenn Algorithmen für uns entscheiden", 2016, S.117 ff. (6. Vorhersagen - Wie aus Korrelationen Prognosen werden)</ref> | ||
===Literaturverzeichnis=== | ===Literaturverzeichnis=== | ||
<references /> | <references /> | ||
Aktuelle Version vom 5. Juli 2024, 09:30 Uhr
Forschungsfrage: Wie kann man mithilfe von Funktionen die Zukunft vorhersagen?
Man kann mit verschiedenen Funktionstypen und Algorithmen unterschiedliche Sachverhalte näherungsweise beschreiben und daraus Prognosen für die Zukunft aufstellen.
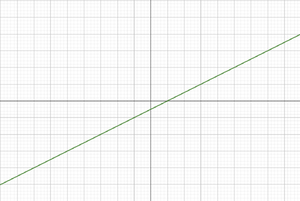
Lineares Wachstum
Lineares Wachstum beschreibt die konstante Zu- oder Abnahme einer Größe . Diese Zunahme wird mithilfe der Konstante beschrieben. Die Differenzengleichung lautet:
Mit der Gleichung (= Anfangsbestand) wird die Rekursion (Zu- oder Abnahme einer Größe in einer bestimmten Zeit) explizit festgelegt. Im Unterricht wird statt dieser Formel oft die Formel , () verwendet.
Graphisch wird das lineare Wachstum durch eine Gerade beschrieben. Lineares Wachstum ist unbegrentzt, wenn ist.
Deshalb können in der Realität nur Abschnitte von natürlichen Vorgängen (beispielsweise das Wachstum von Pflanzen) näherungsweise durch das lineares Wachstum beschrieben werden. Technische Vorgänge (beispielsweise der Füllstand einer Badewanne) werden ebenfalls durch lineares Wachstum beschrieben werden, jedoch gibt es hier meist eine Begrenzung (z.B. bedingt durch das Fassungsvermögen der Badewanne).[1]
Beispielaufgabe lineares Wachstum
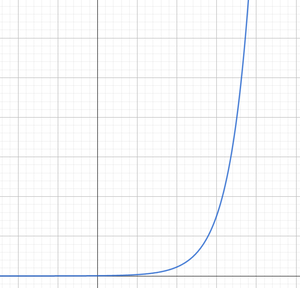
Exponentielles Wachstum
Bei biologischen Wachstumsprozessen ist die Zunahme einer Größe zu Beginn oft proportional zum derzeitigen Bestand
Beispiele: Bakterienwachstum, Wachstum durch Zellteilung, Bevölkerungswachstum, Ausbreitung von Pandemien, Abkühlungen
Die Rekursionsgleichung lautet:
mit als Wachstumsfaktor
und als Wachstumsrate, %,
Lösung der Gleichung:
Die Lösungsgleichung ergibt sich aus der ursprünglichen Gleichung.
wobei der Bestand zum Zeitpunkt ist und der Bestand zum Zeitpunkt [2]
Beispielaufgabe Exponentielles Wachstum
Experiment Exponentielles Wachstum
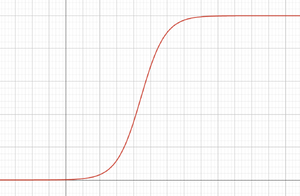
Logistisches Wachstum
Logistische Modelle beschreiben Wachstumsprozesse in der Biologie und der Demographie.
Dadurch werden reale Wachstumsprozesse modelliert, beispielsweise als Basismodell für Bevölkerungs- und Pflanzenwachstum, als Abstatz für ein neues Produkt oder als Anzahl für Krankheiten immunisierter Personen.
Francois Verhulst[3] hat dieses Modell als erster benutzt, um die Bevölkerungsentwicklung zu beschreiben. Allerdings ist dies nur möglich gewesen, da der Belgier Benjamin Gompertz (1825) Vorarbeiten geleistet hatte.
Zu Beginn verläuft der Graph der Funktion meist exponentiell, im weiteren Verlauf flacht er dann ab, sodass die typisch s-förmige Funktion entsteht.
Die Differenzialgleichung lautet:
mit , Kapazitätsgrenze (Sättigungswert und Maximum),
die Größe zum Zeitpunkt t, Größe zu Beginn des Beobachtungszeitraums, Konstante[4]
zum Lösen von Problemen wird meist die Regressionsgleichung verwendet:[5]
Beispielaufgabe logistisches Wachstum
Einsatz von Algorithmen und KI um Vorhersagen zu treffen
Heute werden viele alltägliche Vorhersagen, wie z.B. das Wetter, durch Algorithmen und Big Data (Verwendung von großen Datenmengen) und teilweise sogar mithilfe von KI (Künstliche Intelligenz) von Computer berechnet. Es gibt aber auch weniger bekannte und deutlich komplexere Anwendungszwecke, die große Auswirkungen auf die Gesellschaft haben können:
Google entwickelte beispielsweise Google Flu Trends[6], ein Service, der Grippewellen vorhersagen sollte. Jedoch waren die Vorhersagen, trotz erster Erfolge, meist unzuverlässig. Aus diesem Beispiel lässt sich gut ableiten, was bei der Verwendung von Algorithmen für Vorhersagen unbedingt beachtet werden muss. Um eine genaue Vorhersage treffen zu können, müssen Parameter ständig angepasst werden, da sich die Umstände in der Realität ständig verändern. Außerdem muss auf die Qualität der Daten geachtet werden.[7]
Auch gibt es bereits seit Jahren den Versuch KI und Algorithmen einzusetzen, um Verbrechen vorherzusagen uns somit präventiv zu verhindern, oder Person per Kontrollen auszuwählen. Der Film "Minority Report" (2002)[8], beschäftigte sich mit Ansätzen teilen mit dieser Idee, aber insbesondere mit den Gefahren und Risiken, als auch den sozialen Aspekten. Hauptkrikpunkt ist der soziale Aspekt der fairen Behandlung, da Vorhersagen, deren Grundlage rein aus bestehenden Daten bestehen, nie absolut dem entsprechen, was passieren wird und so unschuldige Menschen bestraft werden könnten. Besonders angreifbar in dieser Hinsicht ist der Einsatz von KI, die ihre Parameter selbst festlegt, da hier nicht einsehbar ist, was diese Parameter besagen. Aufgrund dieser fehlenden Möglichkeit der Überwachung, kann es zu fatalen Fehlentscheidungen (z.B. bei Parametern, die auf Falschinformationen beruhen) oder Diskriminierung(Wohnort und Hautfarbe, könnten fälschlicherweise auch als Parameter genutzt werden) kommen[9].
Blick in die Zukunft
Mit Hilfe der genannten Möglichkeiten sollen aber nicht nur Vorhersagen für kurze, sondern auch für lange Zeitintervalle getroffen werden, um besser auf medizinische, demographische und technologische Ereignisse vorbereitet zu sein. So sind einige positive Beispiele Ausweichempfehlungen bei Stau, neue Fertigungsmethoden in der Produktion oder aber die Nutzung von Smarthome-Systemen. Jedoch gibt es auch negative Aspekte für die KI-Nutzung in der Zukunft, beispielsweise ist eine Abhängigkeit und somit Abgrenzung von realen Menschen, durch eine realistischere Umsetzung verschiedener Programme, möglich. Für die zuverlässige Umsetzung und Nutzung müssen bestehende Programme und Algorithmen jedoch ständig weiterentwickelt, ergänzt und überarbeitet werden.[10]
Literaturverzeichnis
- ↑ Ableitinger, C., "Biomathematische Modelle im Unterricht - Fachwissenschaftliche und didaktische Grundlagen und Unterrichtsmaterialien", 1. Auflage 2010, S.32 ff. (2.1.1 Lineares Wachstum)
- ↑ Ableitinger, C., "Biomathematische Modelle im Unterricht - Fachwissenschaftliche und didaktische Grundlagen und Unterrichtsmaterialien", 1. Auflage 2010, S.32 ff. (2.1.2 Exponentielles Wachstum)
- ↑ https://de.wikipedia.org/wiki/Pierre-Fran%C3%A7ois_Verhulst
- ↑ Ableitinger, C., "mathematiklehren - Erfolgreich unterrichten: Konzepte und Materialien", S.31 ff. (Ein Schritt nach dem anderen - Diskretisieren als Zugang zum logistischen Modell)
- ↑ Ableitinger, C., "Biomathematische Modelle im Unterricht - Fachwissenschaftliche und didaktische Grundlagen und Unterrichtsmaterialien", 1. Auflage 2010, S.43 ff. (2.1.4 Logistische Modelle)
- ↑ https://en.wikipedia.org/wiki/Google_Flu_Trends
- ↑ Drösser, C., "Total berechenbar? Wenn Algorithmen für uns entscheiden", 2016, S.129 ff. (6. Vorhersagen - Wie aus Korrelationen Prognosen werden)
- ↑ https://de.wikipedia.org/wiki/Minority_Report
- ↑ Drösser, C., "Total berechenbar? Wenn Algorithmen für uns entscheiden", 2016, S.118 ff. (6. Vorhersagen - Wie aus Korrelationen Prognosen werden)
- ↑ Drösser, C., "Total berechenbar? Wenn Algorithmen für uns entscheiden", 2016, S.117 ff. (6. Vorhersagen - Wie aus Korrelationen Prognosen werden)