Benutzer:HAG-S15: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 9: | Zeile 9: | ||
<br /> | <br /> | ||
<div style="font-size: 15pt; background-color: #97b8f9; text-align: center; color: white; padding: 5px 100px 5px 100px; margin-top: | <div style="font-size: 15pt; background-color: #97b8f9; text-align: center; color: white; padding: 5px 100px 5px 100px; margin-top: 5px; ">Übung in Learningsnacks</div> | ||
https://www.learningsnacks.de/share/393248/a9f166a09734eea83f17fe2fe338dd6392883634 | [https://www.learningsnacks.de/share/393248/a9f166a09734eea83f17fe2fe338dd6392883634 Ein kleiner Learningsnack von mir] | ||
<br /> | <br /> | ||
| Zeile 34: | Zeile 34: | ||
f(x) = 2x + 3 hat eine Steigung von 2(m) und schneidet die y-Achse bei y=3(b). Die Linie steigt um 2 Einheiten(Kästchen) an, wenn x um 1 Einheit zunimmt. | f(x) = 2x + 3 hat eine Steigung von 2(m) und schneidet die y-Achse bei y=3(b). Die Linie steigt um 2 Einheiten(Kästchen) an, wenn x um 1 Einheit zunimmt. | ||
Aktuelle Version vom 4. Mai 2024, 13:59 Uhr
| Kimi -- Lineare Funktionen | ||
 |
Wissen zu linearen Funktionen | |
|
Lerne etwas dazu | ||
Ein kleiner Learningsnack von mir
Definition:
Lineare Funktionen sind eine grundlegende Art von mathematischen Funktionen, die in vielen Bereichen der Mathematik, Naturwissenschaften und Ingenieurwissenschaften Anwendung finden.
Anwendungen:
Lineare Funktionen finden sich in vielen realen Anwendungen, wie etwa bei Geschwindigkeits-Zeit-Diagrammen, Kostenfunktionen, Einkommensprognosen, Temperaturverläufen und mehr. Sie bieten eine einfache Möglichkeit, Beziehungen zwischen zwei Variablen zu modellieren.
Lineare Funktionen in einem Koordinatensystem
Stellen wir uns ein Koordinatensystem mit einer x-Achse und einer y-Achse vor. Eine lineare Funktion f(x) ist eine gerade Linie, die durch den Ursprung (0,0) verläuft. Die Steigung m bestimmt den Winkel dieser Linie, während der y-Achsenabschnitt b bestimmt, wo die Linie die y-Achse schneidet.
Demnach ist die Formel also:f(x) = mx + b
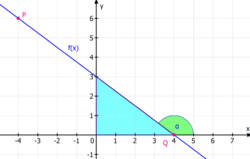
Beispiel für Lineare Funktionen in einem Koordinatensystem:
f(x) = 2x + 3 hat eine Steigung von 2(m) und schneidet die y-Achse bei y=3(b). Die Linie steigt um 2 Einheiten(Kästchen) an, wenn x um 1 Einheit zunimmt.



