Benutzerin:Kübra Uni MS-13/Natürliche Zahlen: Addition und Subtraktion: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 77: | Zeile 77: | ||
}} | }} | ||
{{ | |||
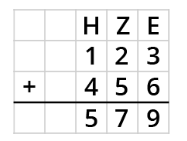
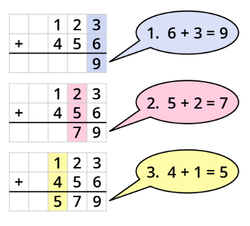
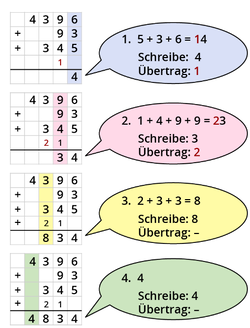
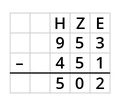
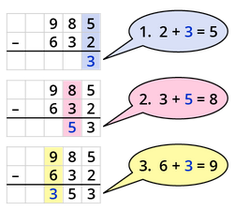
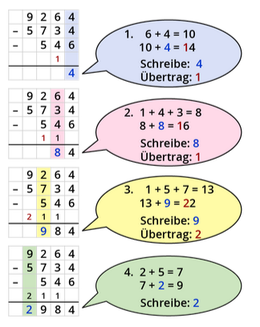
Die '''schriftliche Subtraktion''' hilft dir, größere und mehrere Zahlen zu subtrahieren. | |||
{{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zur schriftlichen Subtraktion|Die '''schriftliche Subtraktion''' hilft dir, größere und mehrere Zahlen zu subtrahieren. | |||
Schreibe die Zahlen immer '''stellengerecht '''untereinander: | Schreibe die Zahlen immer '''stellengerecht '''untereinander: | ||
| Zeile 120: | Zeile 121: | ||
[[Datei:Subtraktion mit Übertrag.png|mini|links|328x328px]] | [[Datei:Subtraktion mit Übertrag.png|mini|links|328x328px]] | ||
|Hervorhebung2 | |||
}} | |||
| Zeile 150: | Zeile 130: | ||
{{Box | [[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 6: Fachbegriffe zur Addition und Subtraktion |{{LearningApp|width=100%|height=500px|app=14302180}}|Üben}} | {{Box | [[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 6: Fachbegriffe zur Addition und Subtraktion |{{LearningApp|width=100%|height=500px|app=14302180}}|Üben}} | ||
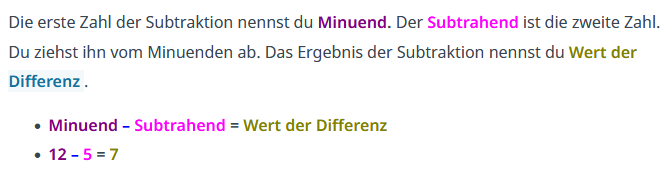
{{ | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz zu Fachbegriffen|'''Addition''' | ||
'''Addition''' | |||
[[Datei:Grundbegriffe der Addition.png|links|1800px|mini]] | [[Datei:Grundbegriffe der Addition.png|links|1800px|mini]] | ||
| Zeile 182: | Zeile 161: | ||
|Hervorhebung2 | |||
}} | |||
{{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 7: Die Rechengesetze|<ggb_applet id="nwufy9pt" width="1000" height="550"/>|Üben}} | {{Box|[[Datei:Icon-pencil-9576.svg|links|rahmenlos|30x30px]]Aufgabe 7: Die Rechengesetze|<ggb_applet id="nwufy9pt" width="1000" height="550"/>|Üben}} | ||
{{ | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Vertauschungsgesetz (Kommutativgesetz)|Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Addieren kannst du die Summanden vertauschen. Das Ergebnis bleibt gleich. | ||
Das '''Vertauschungsgesetz (Kommutativgesetz)''' besagt: Beim Addieren kannst du die Summanden vertauschen. Das Ergebnis bleibt gleich. | |||
'''Beispiel''': 83 + 92 = 92 + 83 | '''Beispiel''': 83 + 92 = 92 + 83 | ||
| Zeile 208: | Zeile 185: | ||
Also ist 100 - 50 + 45 '''nicht '''das gleiche wie 100 - 45 + 50. | Also ist 100 - 50 + 45 '''nicht '''das gleiche wie 100 - 45 + 50. | ||
Beim '''''Subtrahieren '''''kannst du '''Minuend''' und '''Subtrahend''' '''nicht''' vertauschen. Das Vertauschen ergibt unterschiedliche Ergebnisse. | Beim '''''Subtrahieren '''''kannst du '''Minuend''' und '''Subtrahend''' '''nicht''' vertauschen. Das Vertauschen ergibt unterschiedliche Ergebnisse.|Hervorhebung2 | ||
}} | |||
{{ | {{Box|[[Datei:Icon-Pinnnadel.svg|links|rahmenlos|30x30px]] Merksatz Verbindungsgesetz (Assoziativgesetz)|Das '''Verbindungsgesetz (Assoziativgesetz)''' besagt: Beim Addieren kannst du beliebig Klammern setzen oder weglassen. Das Ergebnis bleibt gleich. (Hinweis: Du rechnest zuerst die Klammer wegen Klammer vor Punkt vor Strich aus). | ||
Das '''Verbindungsgesetz (Assoziativgesetz)''' besagt: Beim Addieren kannst du beliebig Klammern setzen oder weglassen. Das Ergebnis bleibt gleich. (Hinweis: Du rechnest zuerst die Klammer wegen Klammer vor Punkt vor Strich aus). | |||
'''Beispiel''': | '''Beispiel''': | ||
| Zeile 234: | Zeile 210: | ||
Also ist (123 - 73) - 27 '''nicht '''das gleiche wie 123 - (73 - 27). | Also ist (123 - 73) - 27 '''nicht '''das gleiche wie 123 - (73 - 27). | ||
Beim '''''Subtrahieren '''''kannst du '''nicht '''beliebig Klammern setzen. Das Setzen von Klammern führt zu unterschiedlichen Ergebnissen. | Beim '''''Subtrahieren '''''kannst du '''nicht '''beliebig Klammern setzen. Das Setzen von Klammern führt zu unterschiedlichen Ergebnissen.|Hervorhebung2 | ||
}} | |||
== Gemischte Aufgaben == | == Gemischte Aufgaben == | ||
=== Textaufgaben === | === Textaufgaben === | ||
Suche bei Anwendungsaufgaben nach '''Signalwörtern'''. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft. | |||
{{Box|[[Datei:Check-Logo.png|links|rahmenlos|30x30px]] Tipp |Suche bei Anwendungsaufgaben nach '''Signalwörtern'''. Übersetze den Text in eine Rechnung, rechne aus und schreibe einen Antwortsatz in dein Heft.|Unterrichtsidee | |||
}} | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
| Zeile 259: | Zeile 238: | ||
* hinzufügen | * hinzufügen | ||
|2=Signalwörter|3=Signalwörter verstecken}} | |2=[[Datei:Check-Logo.png|links|rahmenlos|30x30px]]Signalwörter|3=Signalwörter verstecken}} | ||
==== Waffelverkauf ==== | ==== Waffelverkauf ==== | ||
[[Datei:Waffelverkauf.png|mini]] | [[Datei:Waffelverkauf.png|mini]] | ||
<div style="background:#FFFACD; border:ridge #FFEC8B; padding:10px"> | <div style="background:#FFFACD; border:ridge #FFEC8B; padding:10px"> | ||
Version vom 15. April 2024, 09:46 Uhr
Info
Zahlen begegnen dir jeden Tag: Mitglieder einer AG, Besucher im Stadion, verkaufte Handys. Das sind „natürliche“ Zahlen. Wenn du loszählst, 0, 1, 2, 3 und so weiter, erhältst du die natürlichen Zahlen.
In diesem Lernpfadunterkapitel wiederholst du...
- natürliche Zahlen schriftlich zu addieren und subtrahieren
- Fachbegriffe, Rechengesetze sowie Rechenvorteile zur Addition und Subtraktion
Addition von natürlichen Zahlen
Subtraktion von natürlichen Zahlen
Fachbegriffe und Rechengesetze
Gemischte Aufgaben
Textaufgaben
Diese Signalwörter sagen dir, dass du subtrahierst:
- vermindert
- weniger
- Abnahme
- wegnehmen
- verringern
- abziehen
Diese Signalwörter sagen dir, dass du addierst:
- vermehrt
- mehr
- Zuwachs
- dazu
- hinzufügen
Waffelverkauf
Die 6b hat 120 € in der Klassenkasse. Mit einem Waffelverkauf hat die 6b 48 € verdient. Für ihr Sommerfest gibt die Klasse 80 € für Getränke und Essen aus. Wie viel Geld hat die 6b nach dem Sommerfest in der Klassenkasse?
Rechnung: 120 + 48 - 80 = 168 - 80 = 88
Die 6b hat nach dem Sommerfest 88 € in der Klassenklasse.
Laufen
Aysen trainiert und läuft dreimal in der Woche. Am Montag läuft sie 2 km, am Mittwoch 3 km, aber am Freitag nur 800 m. Wie viel ist sie am Ende der Woche gelaufen?
Wenn in einer Aufgabe Zahlen mit verschiedenen Einheiten vorkommen, wandelst du die Einheiten so um, dass du nur noch eine Einheit hast. Dann kannst du wie gewohnt rechnen.
Rechnung: 2 km + 3 km + 800 m = 2000 m + 3000 m + 800 m = 5800 m
Aysen ist insgesamt 5800 m gelaufen.