Benutzer:Buss-Haskert/Dreiecke/Kongruenzsätze: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
 
(3 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt)
Zeile 5: Zeile 5:
[[Benutzer:Buss-Haskert/Dreiecke/Winkelsumme im Dreieck|2) Winkelsumme im Dreieck]]<br>
[[Benutzer:Buss-Haskert/Dreiecke/Winkelsumme im Dreieck|2) Winkelsumme im Dreieck]]<br>
[[Benutzer:Buss-Haskert/Dreiecke/Dreiecksformen|3) Dreiecksformen]]<br>
[[Benutzer:Buss-Haskert/Dreiecke/Dreiecksformen|3) Dreiecksformen]]<br>
[[Benutzer:Buss-Haskert/Dreiecke/Kongruenzsätze|4) Konstruktion von Dreiecken (Kongruenzsätze)]]}}
[[Benutzer:Buss-Haskert/Dreiecke/Kongruenzsätze|4) Konstruktion von Dreiecken - Kongruenzsätze]]<br>
[[Benutzer:Buss-Haskert/Dreiecke/Umkreis und Inkreis|5) Besondere Linien im Dreieck (Umkreis, Inkreis)]] }}
<br>
<br>
==4) Konstruktion von Dreiecken - Kongruenzsätze==
==4) Konstruktion von Dreiecken - Kongruenzsätze==
Zeile 13: Zeile 14:
<br>
<br>
'''Dreiecke konstruieren: SSS''' - Seite, Seite, Seite<br>
'''Dreiecke konstruieren: SSS''' - Seite, Seite, Seite<br>
Originallink https://www.geogebra.org/m/htean8ru
 
{{Box|1=SSS - Seite, Seite, Seite|2=Zeichne das Dreieck mit a=3,8cm, b=5 cm und c=5,2 cm.<br>
{{Box|1=SSS - Seite, Seite, Seite|2=Zeichne das Dreieck mit a=3,8cm, b=5 cm und c=5,2 cm.<br>
Vergleiche deine Zeichnung mit der deines Nachbarn.<br>
Vergleiche deine Zeichnung mit der deines Nachbarn.<br>
Was fällt dir auf?|3=Arbeitsmethode}}
Was fällt dir auf?|3=Arbeitsmethode}}
Originallink https://www.geogebra.org/m/htean8ru
<ggb_applet id="htean8ru" width="900" height="1000" border="888888" />  
<ggb_applet id="htean8ru" width="900" height="1000" border="888888" />  


<br>
<br>
{{#ev:youtube|KDWOrGAtkC8|800|center}}<br>
{{#ev:youtube|KDWOrGAtkC8|800|center}}<br>
{{Box|Übung 8: SSS|Konstruiere die Dreiecke.
{{Box|Übung 9: SSS|Konstruiere die Dreiecke.
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
Zeile 32: Zeile 34:
|Üben}}
|Üben}}
<br>
<br>
Originallink https://www.geogebra.org/m/x8ywewz7
<ggb_applet id="x8ywewz7" width="2000" height="1800" border="888888" />
<ggb_applet id="x8ywewz7" width="2000" height="1800" border="888888" />
<br>
<br>


{{Box|1=Übung 9: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen a=8,5cm, b=6 cm und c=5cm mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Box|1=Übung 10: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen a=8,5cm, b=6 cm und c=5cm mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne einen Kreis um den Punkt B mit dem Radius d=a=8,5cm.(Kreis mit Mittelpunkt und Radius)|2= 2.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne einen Kreis um den Punkt B mit dem Radius d=a=8,5cm.(Kreis mit Mittelpunkt und Radius)|2= 2.Schritt|3=Verbergen}}
Zeile 41: Zeile 44:
{{Lösung versteckt|1= 4.Schritt: Markiere den Schnittpunkt C der Kreise (Schnittpunkt).Ändere den Namen des oberen Punktes in C. |2= 4.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 4.Schritt: Markiere den Schnittpunkt C der Kreise (Schnittpunkt).Ändere den Namen des oberen Punktes in C. |2= 4.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 5.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 5.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 5.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 5.Schritt|3=Verbergen}}
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br><ggb_applet id="vabdcvsy" width="1416" height="1200" border="888888" /><br>|2=Vergleiche deine Konstruktion|3=Verbergen}}<br>
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br>Originallink https://www.geogebra.org/m/vabdcvsy<br>
<ggb_applet id="vabdcvsy" width="1416" height="1200" border="888888" /><br>|2=Vergleiche deine Konstruktion|3=Verbergen}}<br>


===4.2 WSW===
===4.2 WSW===
Zeile 50: Zeile 54:
Was fällt dir auf?|3=Arbeitsmethode}}
Was fällt dir auf?|3=Arbeitsmethode}}
<br>
<br>
Originallink https://www.geogebra.org/m/rXPkFKrX
<ggb_applet id="rXPkFKrX" width="900" height="700" border="888888" />
<ggb_applet id="rXPkFKrX" width="900" height="700" border="888888" />
<small>(Applet von Pöchtrager)</small>
<small>(Applet von Pöchtrager)</small>
<br>
<br>
{{Box|Übung 10: WSW|Konstruiere die Dreiecke.
{{Box|Übung 11: WSW|Konstruiere die Dreiecke.
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
Zeile 62: Zeile 67:
|Üben}}<br>  
|Üben}}<br>  
{{Lösung versteckt|Du benötigst für die Konstruktion nach WSW immer die an die Seite anliegenden Winkel. Berechne also den fehlenden Winkel mithilfe des Winkelsummensatzes.|Tipp zu Nr. 1 d,e|Verbergen}}<br>
{{Lösung versteckt|Du benötigst für die Konstruktion nach WSW immer die an die Seite anliegenden Winkel. Berechne also den fehlenden Winkel mithilfe des Winkelsummensatzes.|Tipp zu Nr. 1 d,e|Verbergen}}<br>
Originallink https://www.geogebra.org/m/jdsfjqmj
<ggb_applet id="jdsfjqmj" width="1800" height="1500" border="888888" />
<ggb_applet id="jdsfjqmj" width="1800" height="1500" border="888888" />
<br>
<br>
Originallink https://www.geogebra.org/m/sfmg6nrh
<ggb_applet id="sfmg6nrh" width="1432" height="1500" border="888888" />
<ggb_applet id="sfmg6nrh" width="1432" height="1500" border="888888" />
<br>
<br>
Originallink https://www.geogebra.org/m/njxqdgtm
<ggb_applet id="njxqdgtm" width="1432" height="1500" border="888888" /><br>
<ggb_applet id="njxqdgtm" width="1432" height="1500" border="888888" /><br>


{{Box|1=Übung 11: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen c=5cm, <math>\alpha</math>=78° <math>\beta</math>=55° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Box|1=Übung 12: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen c=5cm, <math>\alpha</math>=78° <math>\beta</math>=55° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne den Winkel <math>\alpha</math>=78° (Winkel mit fester Größe), indem du die Strecke f anklickst und dann 78° eingibst.|2= 2.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne den Winkel <math>\alpha</math>=78° (Winkel mit fester Größe), indem du die Strecke f anklickst und dann 78° eingibst.|2= 2.Schritt|3=Verbergen}}
Zeile 76: Zeile 84:
{{Lösung versteckt|1= 6.Schritt: Markiere den Schnittpunkt C der Strahle (Schnittpunkt).|2= 6.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 6.Schritt: Markiere den Schnittpunkt C der Strahle (Schnittpunkt).|2= 6.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 7.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 7.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 7.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 7.Schritt|3=Verbergen}}
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br><ggb_applet id="z7ve2bz7" width="1416" height="1200" border="888888" /><br>|2=Vergleiche deine Konstruktion|3=Verbergen}}
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br>Originallink https://www.geogebra.org/m/z7ve2bz7
<ggb_applet id="z7ve2bz7" width="1416" height="1200" border="888888" /><brhttps://www.geogebra.org/m/z7ve2bz7>|2=Vergleiche deine Konstruktion|3=Verbergen}}
<br>
<br>
===4.3 SWS===
===4.3 SWS===
Zeile 85: Zeile 94:
Was fällt dir auf?|3=Arbeitsmethode}}
Was fällt dir auf?|3=Arbeitsmethode}}
<br>
<br>
Originallink https://www.geogebra.org/m/aasppxtj
<ggb_applet id="aasppxtj" width="1400" height="1000" border="888888" /><br>
<ggb_applet id="aasppxtj" width="1400" height="1000" border="888888" /><br>
<br>
<br>
{{#ev:youtube|micOPq-7Idc|800|center}}
{{#ev:youtube|micOPq-7Idc|800|center}}
<br>
<br>
{{Box|Übung 12: SWS|Konstruiere die Dreiecke.
{{Box|Übung 13: SWS|Konstruiere die Dreiecke.
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
Zeile 100: Zeile 110:
Welchen Winkel bildet der Mast mit dem Boden? Skizziere!|2=Tipp zu Nr. 2|3=Verbergen}}
Welchen Winkel bildet der Mast mit dem Boden? Skizziere!|2=Tipp zu Nr. 2|3=Verbergen}}


Originallink https://www.geogebra.org/m/b9euqhgw
<ggb_applet id="b9euqhgw" width="1416" height="909" border="888888" /><br>
<ggb_applet id="b9euqhgw" width="1416" height="909" border="888888" /><br>
Originallink https://www.geogebra.org/m/cxvgbjzp
<ggb_applet id="cxvgbjzp" width="1416" height="909" border="888888" /><br>
<ggb_applet id="cxvgbjzp" width="1416" height="909" border="888888" /><br>
Originallink https://www.geogebra.org/m/uvjfu6pg
<ggb_applet id="uvjfu6pg" width="1416" height="909" border="888888" /><br>
<ggb_applet id="uvjfu6pg" width="1416" height="909" border="888888" /><br>


{{Box|1=Übung 13: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen b=6,5cm, c=7 cm und <math>\alpha</math>=40° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Box|1=Übung 14: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen b=6,5cm, c=7 cm und <math>\alpha</math>=40° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=7cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=7cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne den Winkel <math>\alpha</math>=40° (Winkel mit fester Größe), indem du die Strecke f anklickst und dann 40° eingibst.|2= 2.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne den Winkel <math>\alpha</math>=40° (Winkel mit fester Größe), indem du die Strecke f anklickst und dann 40° eingibst.|2= 2.Schritt|3=Verbergen}}
Zeile 111: Zeile 124:
{{Lösung versteckt|1= 5.Schritt: Markiere den Schnittpunkt C des Strahls g mit dem Kreis c.|2= 5.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 5.Schritt: Markiere den Schnittpunkt C des Strahls g mit dem Kreis c.|2= 5.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 6.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 6.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 6.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 6.Schritt|3=Verbergen}}
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br><ggb_applet id="bxuhdytg" width="1416" height="1200" border="888888" /><br>|2=Vergleiche deine Konstruktion|3=Verbergen}}<br>
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br>Originallink https://www.geogebra.org/m/bxuhdytg
<ggb_applet id="bxuhdytg" width="1416" height="1200" border="888888" /><br>|2=Vergleiche deine Konstruktion|3=Verbergen}}<br>


===4.4 SsW===
===4.4 SsW===
Zeile 119: Zeile 133:
Vergleiche deine Zeichnung mit der deines Nachbarn.<br>
Vergleiche deine Zeichnung mit der deines Nachbarn.<br>
Was fällt dir auf?|3=Arbeitsmethode}}<br>
Was fällt dir auf?|3=Arbeitsmethode}}<br>
Originallink https://www.geogebra.org/m/QkuY23pW
<ggb_applet id="QkuY23pW" width="900" height="700" border="888888" />
<ggb_applet id="QkuY23pW" width="900" height="700" border="888888" />
<br>
<br>
Originallink https://www.geogebra.org/m/MvzVHSma
<ggb_applet id="MvzVHSma" width="900" height="700" border="888888" /><small>(Applets von Pöchtrager)</small>
<ggb_applet id="MvzVHSma" width="900" height="700" border="888888" /><small>(Applets von Pöchtrager)</small>


Zeile 128: Zeile 144:
<br>
<br>
Nutze die Schieberegler im Applet, damit du siehst, wann es zwei Lösungen gibt. Erkläre!<br>
Nutze die Schieberegler im Applet, damit du siehst, wann es zwei Lösungen gibt. Erkläre!<br>
Originallink https://www.geogebra.org/m/zk7qrqxv
<ggb_applet id="zk7qrqxv" width="1416" height="1200" border="888888" /><br><br>
<ggb_applet id="zk7qrqxv" width="1416" height="1200" border="888888" /><br><br>
{{Box|Übung 14: SsW|Konstruiere die Dreiecke.
{{Box|Übung 15: SsW|Konstruiere die Dreiecke.
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.  
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
* Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
Zeile 141: Zeile 158:
{{Lösung versteckt|1=Hast du nur zwei Seitenlängen gegeben? Nein, du kennst auch einen Winkel!<br>
{{Lösung versteckt|1=Hast du nur zwei Seitenlängen gegeben? Nein, du kennst auch einen Winkel!<br>
Welchen Winkel bildet eine Hauswand immer mit dem Boden? Skizziere!|2=Tipp zu Nr. 3|3=Verbergen}}
Welchen Winkel bildet eine Hauswand immer mit dem Boden? Skizziere!|2=Tipp zu Nr. 3|3=Verbergen}}
Originallink https://www.geogebra.org/m/uvxpg43y
<ggb_applet id="uvxpg43y" width="1416" height="909" border="888888" /><br>
<ggb_applet id="uvxpg43y" width="1416" height="909" border="888888" /><br>
Originallink https://www.geogebra.org/m/zk7qrqxv
<ggb_applet id="zk7qrqxv" width="1416" height="1200" border="888888" /><br>
<ggb_applet id="zk7qrqxv" width="1416" height="1200" border="888888" /><br>
Originallink https://www.geogebra.org/m/y8zvpmrp
<ggb_applet id="y8zvpmrp" width="1416" height="1200" border="888888" /><br>
<ggb_applet id="y8zvpmrp" width="1416" height="1200" border="888888" /><br>
<br>
<br>
{{Box|1=Übung 15: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen b=8,5cm, c=5 cm und <math>\beta</math>=68° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Box|1=Übung 16: Konstruktion mit GeoGebra|2=Konstruiere das Dreieck mit den Seitenlängen b=8,5cm, c=5 cm und <math>\beta</math>=68° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!|3=Üben}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)<br>|2= 1.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne den Winkel <math>\beta</math>=68° (Winkel mit fester Größe), indem du zunächst den Punkt A und dann den Punkt B anklickst, "im Uhrzeigersinn" auswählst und dann die Winkelgröße 68° eingibst.|2= 2.Schritt|3=Verbergen}}
{{Lösung versteckt|1=2.Schritt: Zeichne den Winkel <math>\beta</math>=68° (Winkel mit fester Größe), indem du zunächst den Punkt A und dann den Punkt B anklickst, "im Uhrzeigersinn" auswählst und dann die Winkelgröße 68° eingibst.|2= 2.Schritt|3=Verbergen}}
Zeile 152: Zeile 172:
{{Lösung versteckt|1= 5.Schritt: Markiere den Schnittpunkt C des Strahls g mit dem Kreis.|2= 5.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 5.Schritt: Markiere den Schnittpunkt C des Strahls g mit dem Kreis.|2= 5.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 6.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 6.Schritt|3=Verbergen}}
{{Lösung versteckt|1= 6.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.|2= 6.Schritt|3=Verbergen}}
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br><ggb_applet id="s9hnzzc9" width="1416" height="1200" border="888888" /><br>|2=Vergleiche deine Konstruktion|3=Verbergen}}
{{Lösung versteckt|1=Deine Konstruktion müsste so aussehen:<br> Originallink https://www.geogebra.org/m/s9hnzzc9
<ggb_applet id="s9hnzzc9" width="1416" height="1200" border="888888" /><br>|2=Vergleiche deine Konstruktion|3=Verbergen}}


==Vermischte Übungen und Anwendungsaufgaben==
==Vermischte Übungen und Anwendungsaufgaben==
{{Box|1=Übung 16: Übungen zu Grundkonstruktionen (bei Bedarf)|2=Bearbeite die Aufgaben in deinem Heft und vergleiche deine Lösungen.<br>
{{Box|1=Übung 17: Übungen zu Grundkonstruktionen (bei Bedarf)|2=Bearbeite die Aufgaben in deinem Heft und vergleiche deine Lösungen.<br>
* [https://www.geogebra.org/m/xw4njYUy#chapter/262145 '''Übungen GeoGebra''']
* [https://www.geogebra.org/m/xw4njYUy#chapter/262145 '''Übungen GeoGebra''']
* [http://www.mathe-trainer.de/Klasse7/Geometrie/Konstruktionen/Block1/Aufgaben.htm '''mathe-trainer''']|3=Üben}}
* [http://www.mathe-trainer.de/Klasse7/Geometrie/Konstruktionen/Block1/Aufgaben.htm '''mathe-trainer''']|3=Üben}}
<br>
<br>
{{Box|Übung 17: Anwendungsaufgaben|In unserer Umgebung gibt es viele Fragestellungen, die sich mithilfe von Dreieckskonstruktionen beantworten lassen. Gehe bei der Lösung schrittweise vor:
{{Box|Übung 18: Anwendungsaufgaben|In unserer Umgebung gibt es viele Fragestellungen, die sich mithilfe von Dreieckskonstruktionen beantworten lassen. Gehe bei der Lösung schrittweise vor:
* Lies die Aufgabenstellung genau.  
* Lies die Aufgabenstellung genau.  
* Zeichne eine Planfigur (Dreieck) und beschrifte es mit den im Text gegebenen Größen. Wähle dazu einen passenden Maßstab, z.B. 1m in Wirklichkeit entspricht 1cm in der Zeichnung.
* Zeichne eine Planfigur (Dreieck) und beschrifte es mit den im Text gegebenen Größen. Wähle dazu einen passenden Maßstab, z.B. 1m in Wirklichkeit entspricht 1cm in der Zeichnung.

Aktuelle Version vom 21. Dezember 2023, 08:41 Uhr

Schullogo HLR.jpg
zurück zur Seite der Herta-Lebenstein-Realschule


4) Konstruktion von Dreiecken - Kongruenzsätze

Material FLINK Team auf GeoGebra https://www.geogebra.org/m/cpgvg6rg (noch einfügen)

4.1 SSS


Dreiecke konstruieren: SSS - Seite, Seite, Seite


SSS - Seite, Seite, Seite

Zeichne das Dreieck mit a=3,8cm, b=5 cm und c=5,2 cm.
Vergleiche deine Zeichnung mit der deines Nachbarn.

Was fällt dir auf?

Originallink https://www.geogebra.org/m/htean8ru

GeoGebra


Video laden
YouTube


Übung 9: SSS

Konstruiere die Dreiecke.

  • Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.
  • Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
  • Überprüfe deine Lösung im Heft mithilfe des GeoGebra-Applets unter dieser Übung, indem du die Schieberegler passend einstellst.

Löse Buch

  • S. 82 Nr. 1a
  • S. 82 Nr. 2
  • S. 82 Nr. 3


Originallink https://www.geogebra.org/m/x8ywewz7

GeoGebra



Übung 10: Konstruktion mit GeoGebra
Konstruiere das Dreieck mit den Seitenlängen a=8,5cm, b=6 cm und c=5cm mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!
1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)
2.Schritt: Zeichne einen Kreis um den Punkt B mit dem Radius d=a=8,5cm.(Kreis mit Mittelpunkt und Radius)
3.Schritt: Zeichne einen Kreis um den Punkt A mit dem Radius e=b=6 cm.(Kreis mit Mittelpunkt und Radius)
4.Schritt: Markiere den Schnittpunkt C der Kreise (Schnittpunkt).Ändere den Namen des oberen Punktes in C.
5.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.

Deine Konstruktion müsste so aussehen:
Originallink https://www.geogebra.org/m/vabdcvsy

GeoGebra


4.2 WSW


Dreiecke konstruieren: WSW - Winkel, eingeschlossene Seite, Winkel

WSW - Winkel, eingeschlossene Seite, Winkel

Zeichne das Dreieck mit c=6 cm, =40° und =70°.
Vergleiche deine Zeichnung mit der deines Nachbarn.

Was fällt dir auf?


Originallink https://www.geogebra.org/m/rXPkFKrX

GeoGebra

(Applet von Pöchtrager)

Übung 11: WSW

Konstruiere die Dreiecke.

  • Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.
  • Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
  • Überprüfe deine Lösung im Heft mithilfe der GeoGebra-Applets unter dieser Übung, indem du die Schieberegler passend einstellst. Wähle das passende Applet aus.

Löse Buch

  • S. 83 Nr. 1
  • S. 83 Nr. 2


Du benötigst für die Konstruktion nach WSW immer die an die Seite anliegenden Winkel. Berechne also den fehlenden Winkel mithilfe des Winkelsummensatzes.


Originallink https://www.geogebra.org/m/jdsfjqmj

GeoGebra


Originallink https://www.geogebra.org/m/sfmg6nrh

GeoGebra


Originallink https://www.geogebra.org/m/njxqdgtm

GeoGebra



Übung 12: Konstruktion mit GeoGebra
Konstruiere das Dreieck mit den Seitenlängen c=5cm, =78° =55° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!
1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)
2.Schritt: Zeichne den Winkel =78° (Winkel mit fester Größe), indem du die Strecke f anklickst und dann 78° eingibst.
3.Schritt: Zeichne den Strahl g durch die Punkte A und B'.
4.Schritt: Zeichne den Winkel =55° (Winkel mit fester Größe), indem du die zunächst den Punkt A und dann den Punkt B anklickst, "im Uhrzeigersinn" auswählst und dann 55° eingibst.
5.Schritt: Zeichne den Strahl h durch die Punkte B und A'.
6.Schritt: Markiere den Schnittpunkt C der Strahle (Schnittpunkt).
7.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.

Deine Konstruktion müsste so aussehen:
Originallink https://www.geogebra.org/m/z7ve2bz7

GeoGebra
<brhttps://www.geogebra.org/m/z7ve2bz7>


4.3 SWS


Dreiecke konstruieren: SWS- Seite, eingeschlossener Winkel, Seite

SWS -Seite, eingeschlossener Winkel, Seite

Zeichne das Dreieck mit =50°, b=4,4cm und c=5,5cm.
Vergleiche deine Zeichnung mit der deines Nachbarn.

Was fällt dir auf?


Originallink https://www.geogebra.org/m/aasppxtj

GeoGebra



Video laden
YouTube


Übung 13: SWS

Konstruiere die Dreiecke.

  • Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.
  • Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
  • Überprüfe deine Lösung im Heft mithilfe der GeoGebra-Applets unter dieser Übung, indem du die Schieberegler passend einstellst. Wähle das passende Applet aus.

Löse Buch

  • S. 84 Nr. 1
  • S. 84 Nr. 2


Hast du nur zwei Seitenlängen gegeben? Nein, du kennst auch einen Winkel!

Welchen Winkel bildet der Mast mit dem Boden? Skizziere!

Originallink https://www.geogebra.org/m/b9euqhgw

GeoGebra


Originallink https://www.geogebra.org/m/cxvgbjzp

GeoGebra


Originallink https://www.geogebra.org/m/uvjfu6pg

GeoGebra



Übung 14: Konstruktion mit GeoGebra
Konstruiere das Dreieck mit den Seitenlängen b=6,5cm, c=7 cm und =40° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!
1.Schritt: Zeichne die Strecke f=c=7cm.(Strecke mit fester Länge)
2.Schritt: Zeichne den Winkel =40° (Winkel mit fester Größe), indem du die Strecke f anklickst und dann 40° eingibst.
3.Schritt: Zeichne den Strahl g durch die Punkte A und B'.
4.Schritt: Zeichne um den Punkt A einen Kreis mit dem Radius c=b=6,5cm.(Kreis mit Mittelpunkt und Radius)
5.Schritt: Markiere den Schnittpunkt C des Strahls g mit dem Kreis c.
6.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.

Deine Konstruktion müsste so aussehen:
Originallink https://www.geogebra.org/m/bxuhdytg

GeoGebra


4.4 SsW


Dreiecke konstruieren: SsW - Seite, Seite, (der längeren Seite gegenüberliegender) Winkel

SsW - lange Seite, kurze Seite, Winkel

Zeichne das Dreieck mit =35°, a=5,6cm und c=4,7cm.
Vergleiche deine Zeichnung mit der deines Nachbarn.

Was fällt dir auf?


Originallink https://www.geogebra.org/m/QkuY23pW

GeoGebra


Originallink https://www.geogebra.org/m/MvzVHSma

GeoGebra

(Applets von Pöchtrager)


Video laden
YouTube


Nutze die Schieberegler im Applet, damit du siehst, wann es zwei Lösungen gibt. Erkläre!
Originallink https://www.geogebra.org/m/zk7qrqxv

GeoGebra



Übung 15: SsW

Konstruiere die Dreiecke.

  • Zeichne zunächst eine Planfigur und trage dort farbig die gegebenen Größen ein.
  • Konstruiere das Dreieck mit Zirkel und Lineal. Zeichne mit Bleistift! Die nötigen Schritte kannst du im GeoGebra-Applet oben noch einmal nachschauen.
  • Überprüfe deine Lösung im Heft mithilfe der GeoGebra-Applets unter dieser Übung, indem du die Schieberegler passend einstellst. Wähle das passende Applet aus.

Löse Buch

  • S. 85 Nr. 1
  • S. 85 Nr. 2
  • S. 85 Nr. 3


Nutze die Schieberegler im Applet oben, damit du siehst, wann es zwei Lösungen gibt. Erkläre!


Hast du nur zwei Seitenlängen gegeben? Nein, du kennst auch einen Winkel!

Welchen Winkel bildet eine Hauswand immer mit dem Boden? Skizziere!

Originallink https://www.geogebra.org/m/uvxpg43y

GeoGebra


Originallink https://www.geogebra.org/m/zk7qrqxv

GeoGebra


Originallink https://www.geogebra.org/m/y8zvpmrp

GeoGebra



Übung 16: Konstruktion mit GeoGebra
Konstruiere das Dreieck mit den Seitenlängen b=8,5cm, c=5 cm und =68° mit GeoGebra. Zeichne zunächst eine Planfigur in dein Heft!
1.Schritt: Zeichne die Strecke f=c=5cm.(Strecke mit fester Länge)
2.Schritt: Zeichne den Winkel =68° (Winkel mit fester Größe), indem du zunächst den Punkt A und dann den Punkt B anklickst, "im Uhrzeigersinn" auswählst und dann die Winkelgröße 68° eingibst.
3.Schritt: Zeichne den Strahl g durch die Punkte B und A'.
4.Schritt: Zeichne um den Punkt A einen Kreis mit dem Radius b=8,5cm.(Kreis mit Mittelpunkt und Radius)
5.Schritt: Markiere den Schnittpunkt C des Strahls g mit dem Kreis.
6.Schritt: Zeichne mit "Vieleck" das Dreieck ABC.

Deine Konstruktion müsste so aussehen:
Originallink https://www.geogebra.org/m/s9hnzzc9

GeoGebra

Vermischte Übungen und Anwendungsaufgaben

Übung 17: Übungen zu Grundkonstruktionen (bei Bedarf)

Bearbeite die Aufgaben in deinem Heft und vergleiche deine Lösungen.


Übung 18: Anwendungsaufgaben

In unserer Umgebung gibt es viele Fragestellungen, die sich mithilfe von Dreieckskonstruktionen beantworten lassen. Gehe bei der Lösung schrittweise vor:

  • Lies die Aufgabenstellung genau.
  • Zeichne eine Planfigur (Dreieck) und beschrifte es mit den im Text gegebenen Größen. Wähle dazu einen passenden Maßstab, z.B. 1m in Wirklichkeit entspricht 1cm in der Zeichnung.
  • Notiere, um welchen Kongruenzsatz es sich handelt (SSS, WSW, SWS oder SsW).
  • Konstruiere das Dreieck und miss die gesuchte Größe.
  • Notiere einen Antwortsatz, in dem du die passende Maßeinheit (z.B. m) verwendest.

Löse die Aufgaben aus dem Buch

  • S. 92, Nr. 12
  • S. 92, Nr. 13
  • S. 92, Nr. 14 (schwer!)
  • S. 93, Nr. 5 links
  • S. 93, Nr. 5 rechts


Trage in deiner Planfigur die gegebenen Größen ein. Du siehst, es sind zwei Winkel und die eingeschlossene Seite gegebenen. Konstruiere also mit WSW.

Der Maßstab 1:2000 bedeutet, dass 1cm in der Zeichnung 2000cm in Wirklichkeit sind.
Also sind 2000cm=20m in Wirklichkeit 1cm in der Zeichnung.
10m in Wirklickeit sind also 0,5 cm in der Zeichnung.

Also sind 150m in Wirklichkeit 7,5cm in der Zeichnung.

Du markierst in der Planfigur den Winkel =28° als gegeben und die Seite c=7,5cm (berechnet mit dem Maßstab, Tipp 1).
Nun fehlt eine weitere Angabe: Du kennst auch den Winkel !
In welchem Winkel zum Boden werden Windräder aufgebaut?

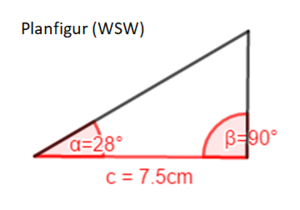
S. 92 Nr. 13 Planfigur neu.png

Nun konstruierst du das Dreieck mit der Konstruktion nach WSW. Miss die Länge der Seite a und rechne mithilfe des Maßstabes die Länge in Wirklichkeit um. Aber Vorsicht, du bist noch nicht fertig!

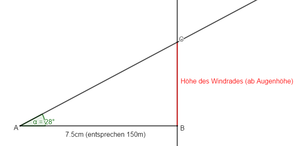
S. 92 Nr. 13 Skizze.png

Zum Schluss musst du noch die Körpergröße von 1,60m zur gemessenen Höhe im Dreieck (schon in m umgewandelt) addieren.

Lösung: Die gemessene Höhe beträgt ca. 4cm, dies sind 4∙20m = 80 m in Wirklichkeit. Mit der Körpergröße von 1,60m ist das Windrad also 81,60 m hoch.

Der Maßstab 1:500 bedeutet, dass 1cm in der Zeichnung 500 cm in Wirklichkeit sind.
500cm = 5m in der Wirklichkeit sind 1cm in der Zeichnung.
1m in Wirklichkeit sind also 0,2 cm in der Zeichnung und
28 m in Wirklichkeit sind 5,6 cm in der Zeichnung.

Auch hier kennst du den Winkel zwischen Turm und Boden.

Zeichne in Höhe der Turmspitze eine parallele Hilfslinie zum "Boden" ein.
Trage die angegebenen Winkel an und verlängere die freien Schenkel bis zum "Boden".

Wenn du alles richtig gemacht hast, ist die Strecke von A nach B (der "See") 7,6 cm lang. Rechne die Länge mit Hilfe des Maßstabs wieder in m um. Du erhältst eine Seebreite von 38 m.
Kontruiere mit SWS. Die Lösung findest du hinten im Buch! (Rückspiegel)


Ergänzung: Umkreis und Inkreis von Dreiecken
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Dreiecke/Kongruenzsätze&oldid=91533“