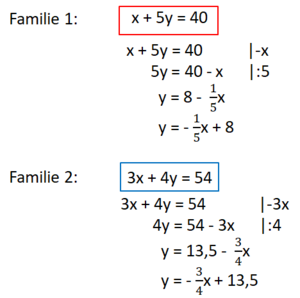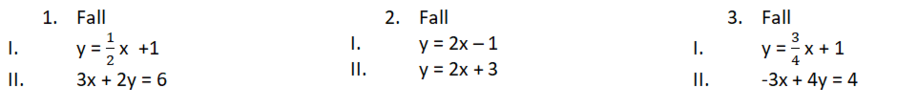Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme zeichnerisch lösen: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 135: | Zeile 135: | ||
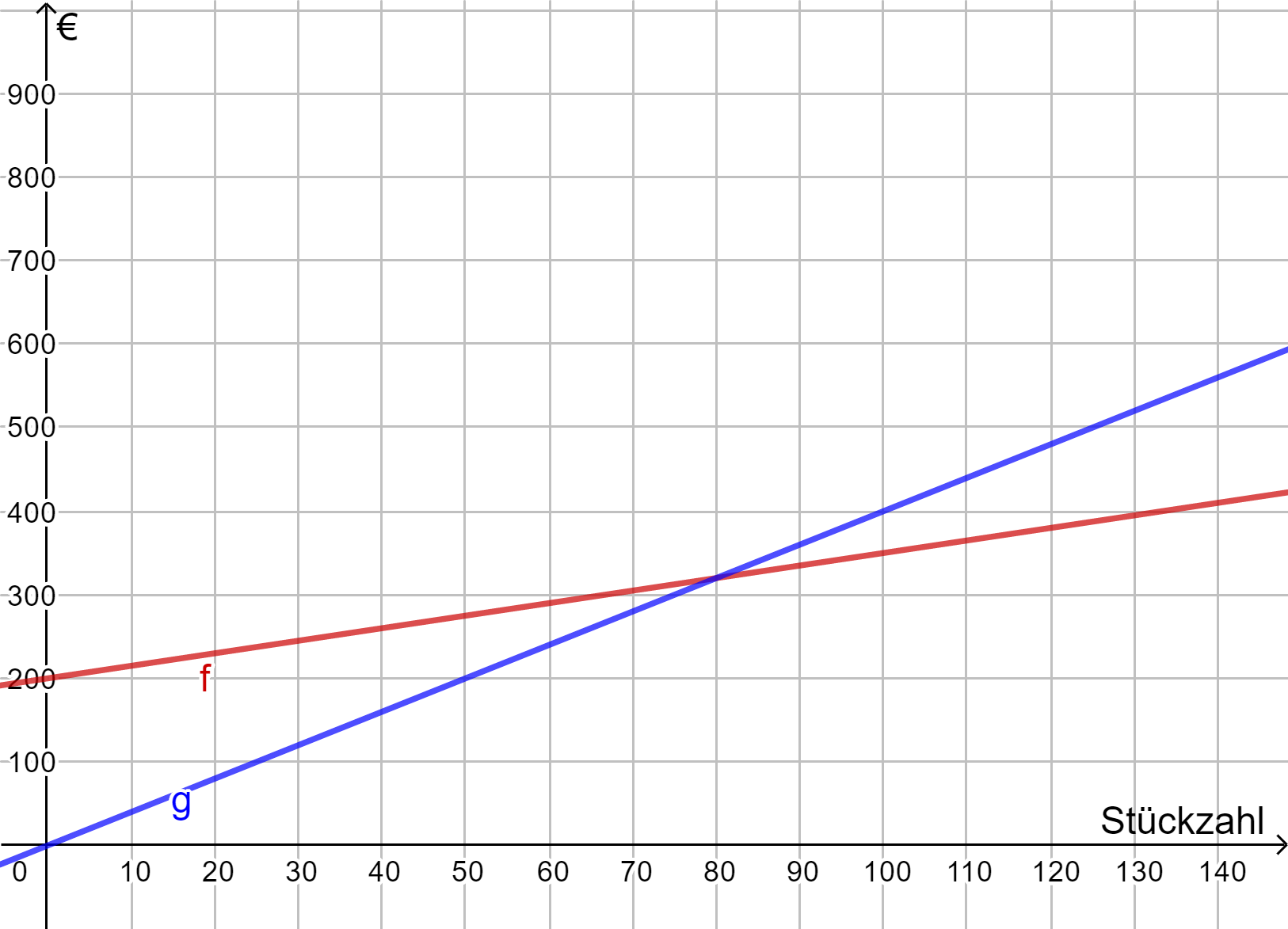
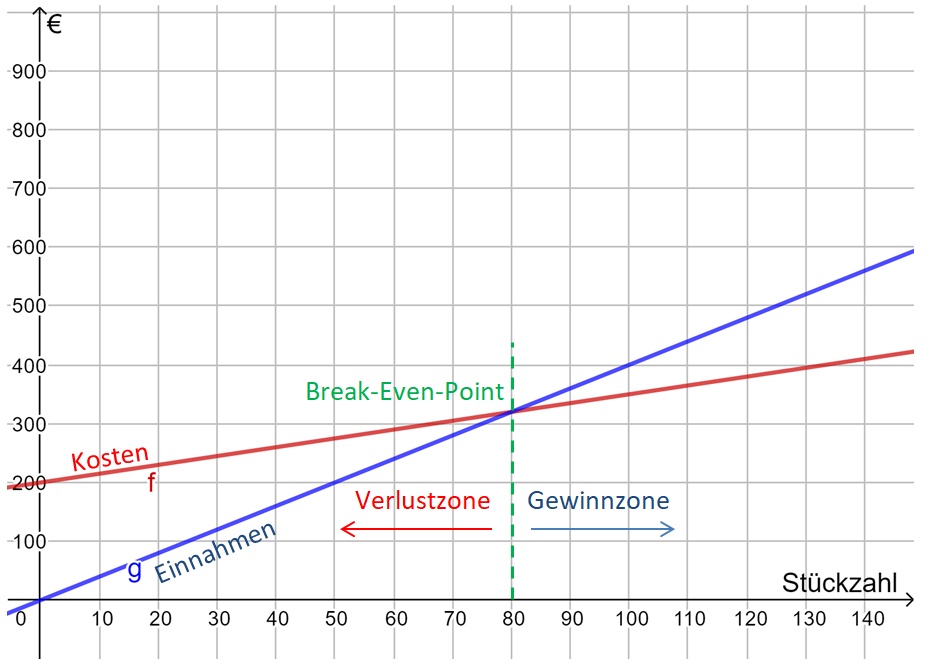
{{Box|Übung 8: Anwendung: Break-even-Point| Eine Firma stellt Maschinenteile her. Die Fixkosten dafür betragen 200€ und pro Teil entstehen zusätzlich variable Kosten von 1,50€.<br>Jedes Teil wird für 4,00€ verkauft.<br>a) Gib die Funktionsgleichungen für die Kosten und für den Erlös an.<br>b) Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Break-Even-Point ab.<br>c) Formuliere selbst eine Aufgabe zu diesem Sachverhalt und beantworte diese mithilfe der Zeichnung.|Üben}} | {{Box|Übung 8: Anwendung: Break-even-Point| Eine Firma stellt Maschinenteile her. Die Fixkosten dafür betragen 200€ und pro Teil entstehen zusätzlich variable Kosten von 1,50€.<br>Jedes Teil wird für 4,00€ verkauft.<br>a) Gib die Funktionsgleichungen für die Kosten und für den Erlös an.<br>b) Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Break-Even-Point ab.<br>c) Formuliere selbst eine Aufgabe zu diesem Sachverhalt und beantworte diese mithilfe der Zeichnung.|Üben}} | ||
An dieser Aufgabe merkst du, dass die Mathematik eine Hilfswissenschaft für andere Gebiete, z.B. Sozialwissenschaften, ist. Noch mehr Aufgaben zur Berechnung des Break-Even-Points findest du hier: [[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Break-Even-Point| Übungen zur Berechnung des Break-Even-Points]] | An dieser Aufgabe merkst du, dass die Mathematik eine Hilfswissenschaft für andere Gebiete, z.B. Sozialwissenschaften, ist. Noch mehr Aufgaben zur Berechnung des Break-Even-Points findest du hier: | ||
<br> [[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Break-Even-Point| Übungen zur Berechnung des Break-Even-Points]] | |||
{{Lösung versteckt|1=Tipp zu a)<br>Die Kosten setzen sich zusammen aus den Fixkosten und den variablen Kosten. x sei die Stückzahl, die gefertigt wird. Dann lautet die zugehörige Funktionsgleichung f(x)=1,5x+200.<br>Die Funktionsgleichung für den Erlös lautet g(x)=4x|2=Tipp zu a)|3=Verbergen}} | {{Lösung versteckt|1=Tipp zu a)<br>Die Kosten setzen sich zusammen aus den Fixkosten und den variablen Kosten. x sei die Stückzahl, die gefertigt wird. Dann lautet die zugehörige Funktionsgleichung f(x)=1,5x+200.<br>Die Funktionsgleichung für den Erlös lautet g(x)=4x|2=Tipp zu a)|3=Verbergen}} | ||
| Zeile 145: | Zeile 146: | ||
Das Angebot sind alle Güter und Dienstleitungen, die erworben werden können. Die Nachfrage ist der Bedarf nach einem Produkt. | Das Angebot sind alle Güter und Dienstleitungen, die erworben werden können. Die Nachfrage ist der Bedarf nach einem Produkt. | ||
Hier findest du mehr Informationen zum Gleichgewichtspreis (Angebot und Nachfrage) | Hier findest du mehr Informationen zum Gleichgewichtspreis (Angebot und Nachfrage)<br> | ||
[[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Gleichgewichtspreis| Gleichgewichtspreis]] | [[Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Gleichgewichtspreis| Gleichgewichtspreis]]<br> | ||
<br> | |||
{{Fortsetzung|vorher=Startseite Lineare Gleichungssysteme|vorherlink=Benutzer:Buss-Haskert/Lineare Gleichungssysteme|weiter=4) Lineare Gleichungssysteme rechnerisch lösen|weiterlink=Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme rechnerisch lösen}} | {{Fortsetzung|vorher=Startseite Lineare Gleichungssysteme|vorherlink=Benutzer:Buss-Haskert/Lineare Gleichungssysteme|weiter=4) Lineare Gleichungssysteme rechnerisch lösen|weiterlink=Benutzer:Buss-Haskert/Lineare Gleichungssysteme/Lineare Gleichungssysteme rechnerisch lösen}} | ||
Aktuelle Version vom 17. Juli 2023, 16:22 Uhr
1) Lineare Gleichungen mit zwei Variablen
2) Lineare Gleichungssysteme
3) Lineare Gleichungssysteme zeichnerisch lösen
4) Lineare Gleichungssysteme rechnerisch lösen
5) Modellieren
6) Checkliste
3) Lineare Gleichungssysteme zeichnerisch lösen
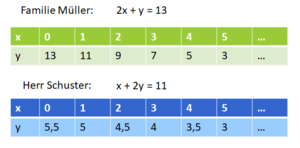
Lege die Bedeutung der Variablen fest, z.B. x - Preis pro Erwachsener, y - Preis pro Kind.
Stelle nun jeweils eine passende Gleichung auf. Nutze zur Lösung verschiedene Darstellungen: Wertetabellen und Graphen.
I. 2x + y = 13
II. x + 2y = 11
Das Video fasst die Schritte noch einmal zusammen:
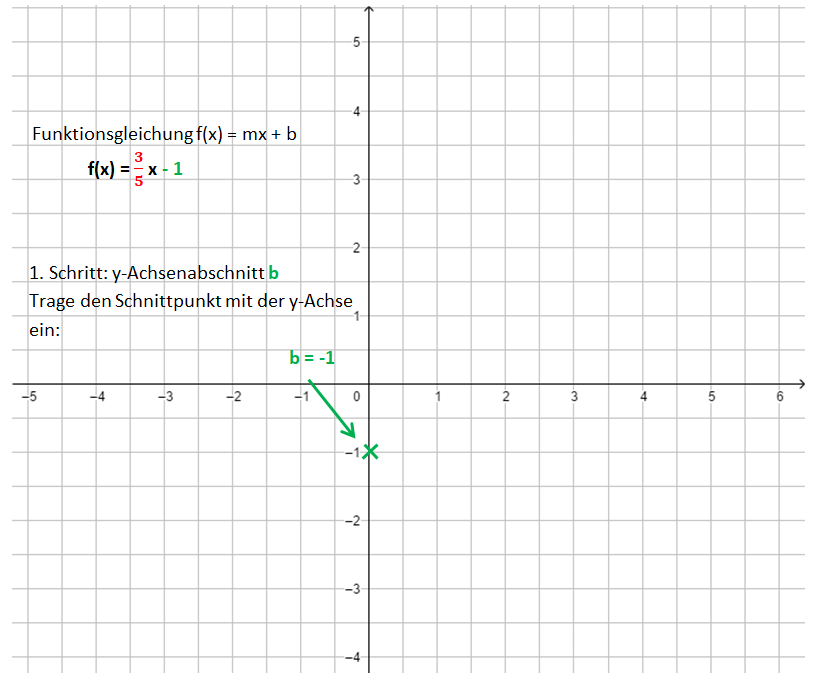
Wie zeichne ich den Graphen, wenn die Funktionsgleichung gegeben ist?
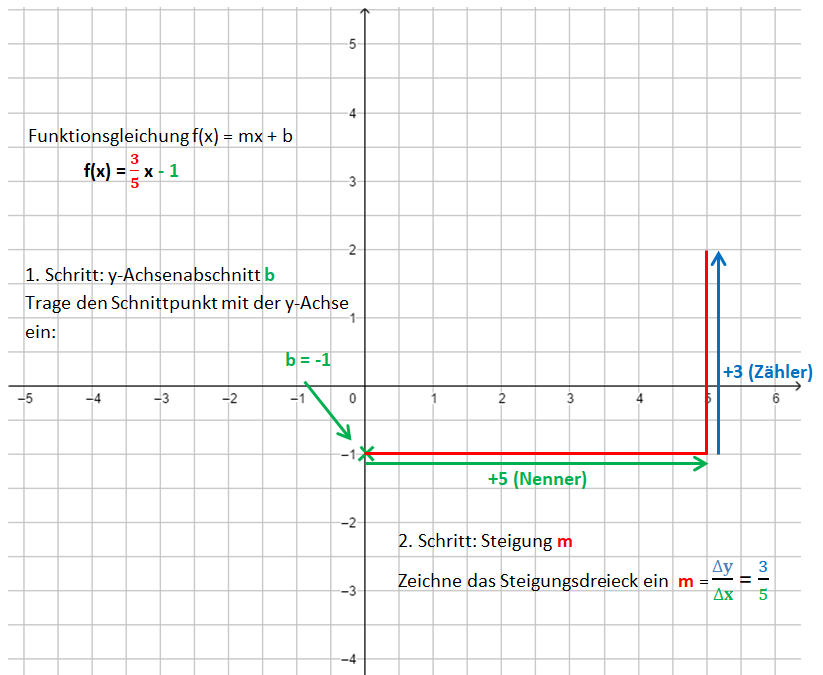
1. Schritt: Zeichne den y-Achsenabschnitt b ein: P(0|b)
2. Schritt: Zeichne das Steigungsdreieck ein. Starte im Punkt P. Der Nenner gibt an, wie viele Einheiten du nach rechts gehst, der Zähler, wie viele Einheiten nach oben (unten).
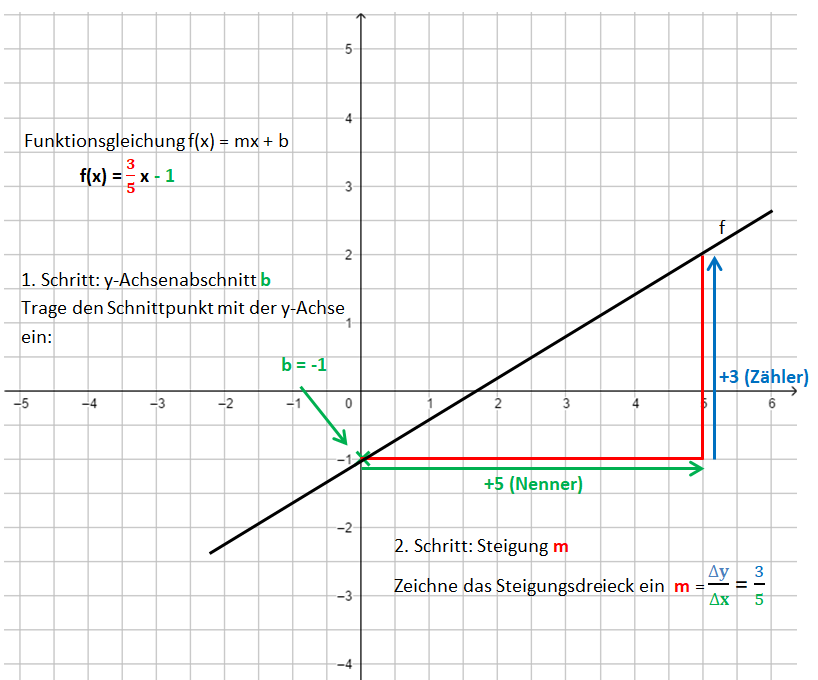
3. Schritt: Zeichne die Gerade durch die so erhaltenen Punkte.
Die Bilder zeigen das Vorgehen für die Funktionsgleichung f(x) = x - 1.
Wie zeichne ich den Graphen zu einer Funktionsgleichung: Videos
Lösung zu S.14 Nr. 2a Schritt für Schritt:

direkter Link: https://www.geogebra.org/m/kb3en6sj

Applet von just01120
Löse schrittweise, wie oben beschrieben:
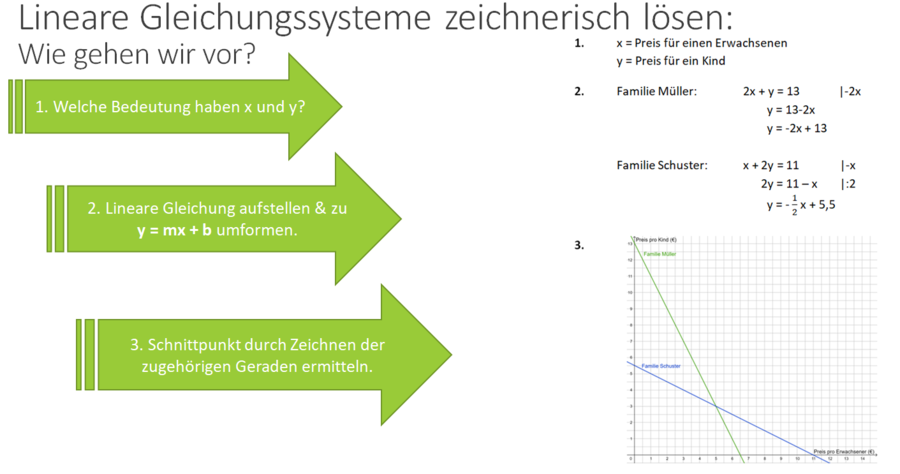
1. Lege die Bedeutung der Variablen fest
2. Stelle zwei lineare Gleichungen auf und forme sie so um, dass sie die Form y=mx+b haben.
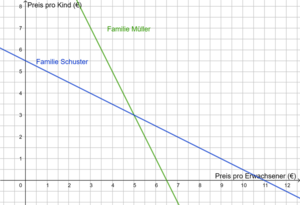
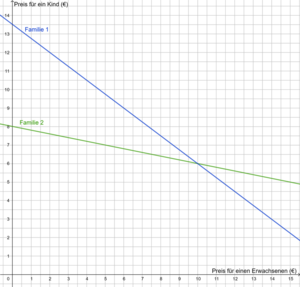
3. Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Schnittpunkt ab. Die Koordinaten des Schnittpunktes sind die Lösung des Gleichungssystems.
x = Preis für einen Erwachsenen
y = Preis für ein Kind
Löse schrittweise, wie oben beschrieben:
1. Lege die Bedeutung der Variablen fest
2. Stelle zwei lineare Gleichungen auf und forme sie so um, dass sie die Form y=mx+b haben.
3. Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Schnittpunkt ab. Die Koordinaten des Schnittpunktes sind die Lösung des Gleichungssystems.
x = Leihdauer (in Tagen)
y = Preis (in €)
I. y = 3x + 10
II. y = 5x
Gib die Funktionsgleichungen bei GeoGebra ein und vergleiche mit deiner Lösung
GeoGebra Grafikrechner
Löse schrittweise, wie oben beschrieben:
1. Lege die Bedeutung der Variablen fest
2. Stelle zwei lineare Gleichungen auf und forme sie so um, dass sie die Form y=mx+b haben.
3. Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Schnittpunkt ab. Die Koordinaten des Schnittpunktes sind die Lösung des Gleichungssystems.
x = Anzahl der Arbeitsstunden
y = Preis (in €)
I. y = 25x + 125
II. y = 30x
Einteilung der Koordinatenachsen: 1cm entspricht 10 Stunden
Gib die Funktionsgleichungen bei GeoGebra ein und vergleiche mit deiner Lösung
GeoGebra Grafikrechner
Löse schrittweise, wie oben beschrieben:
1. Lege die Bedeutung der Variablen fest
2. Stelle zwei lineare Gleichungen auf und forme sie so um, dass sie die Form y=mx+b haben.
3. Zeichne die zugehörigen Graphen in ein Koordinatensystem und lies den Schnittpunkt ab. Die Koordinaten des Schnittpunktes sind die Lösung des Gleichungssystems.
x = Leihdauer (in Stunden)
y = Preis (in €)
I. y = 12x + 100
II. y = 20x
Wähle die Einteilung der Koordinatenachsen geschickt.
Gib die Funktionsgleichungen bei GeoGebra ein und vergleiche mit deiner Lösung
GeoGebra Grafikrechner
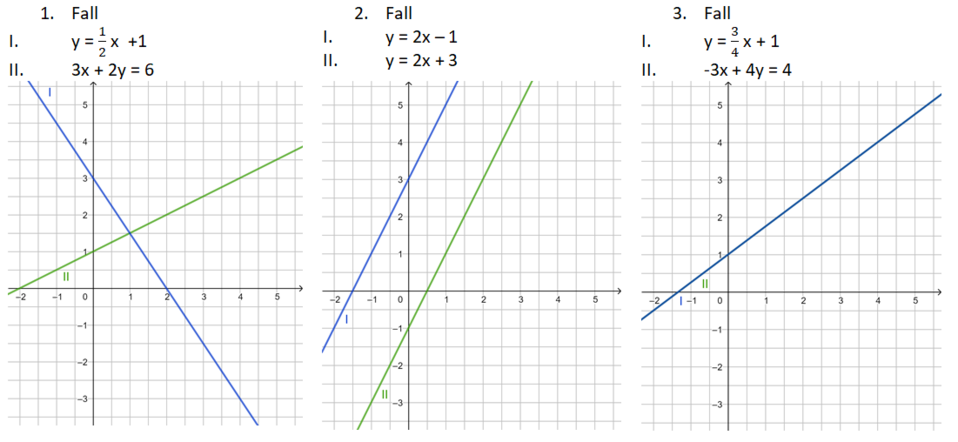
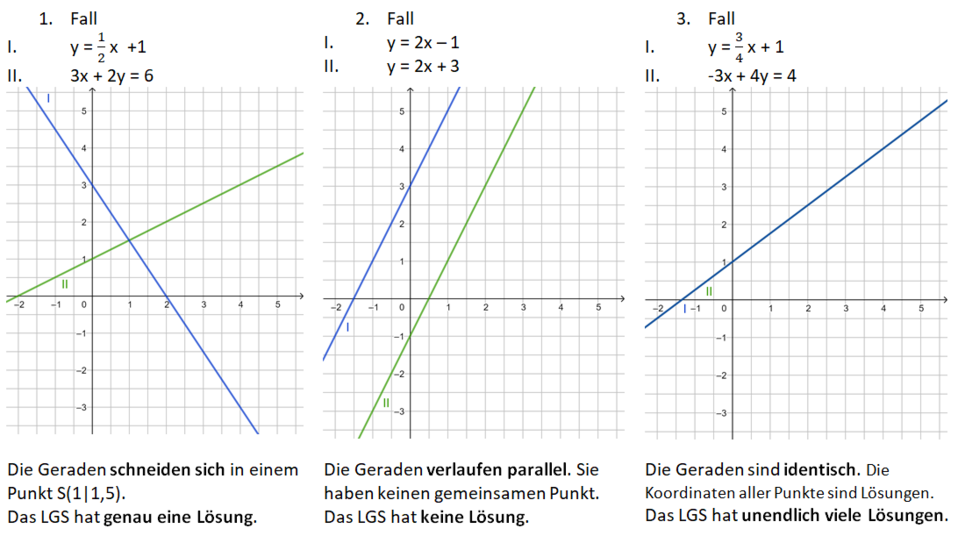
Anzahl der Lösungen linearer Gleichungssysteme
Um ein Gleichungssystem zeichnerisch lösen zu können, musst du die Gleichungen in die Form y = mx + b bringen. Dann kannst du die Geraden mit dem y-Achsenabschnitt b und dem Steigungsdreieck (für m) zeichnen.

Beim 2. Fall sind die Gleichungen schon in der Form y = mx+b gegeben.

Beispiel zu b)
2x+y=4
x+y=3
y=-2x+4
y=-x+3
Nun kannst du mithilfe der Steigung m und des y-Achsenabschnittes b entscheiden, ob die Geraden sich schneiden (eine Lösung), parallel verlaufen (keine Lösung) oder sogar identisch sind (unendlich viele Lösungen).
Stelle mithilfe den Schieberegler so ein, dass die beiden Geraden keinen Schnittpunkt S haben. Wie groß ist dann die Steigung m? Was fällt dir auf? Begründe!

y=2x+5
y=2x-5
Die Graphen dieser Funktionen verlaufen parallel, da die Steigung m=2 gleich ist, der y-Achsenabschnitt aber verschieden ist (b=+5 und b=-5).
Bringe die erste Gleichung zunächst in die Form y = mx + b:
I. y + ___x = 3 |-___x
y = - ___x + 3
Bringe auch hier die erste Gleichung in die Form y = mx + b:
2y = __x + 3 |:2
y = ___x + 1,5, wobei die Lücke m:2 beträgt.
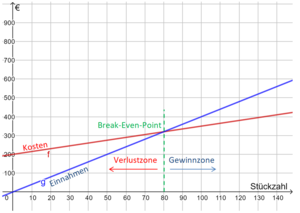
Erweiterung: Break-Even-Point
Um bei einer Produktion festzustellen, ab wann die Firma einen Gewinn erzielt, müssen die Kosten mit den Erlösen (Einnahmen) verglichen werden. Der Break-Even-Point ist der Punkt, an die Einnahmen und Kosten gleich hoch sind. An dieser Stelle wird kein Gewinn aber auch kein Verlust erwirtschaftet, da die Kosten und die Erlöse genau gleich sind. Ab hier beginnt also die Gewinnzone.
An dieser Aufgabe merkst du, dass die Mathematik eine Hilfswissenschaft für andere Gebiete, z.B. Sozialwissenschaften, ist. Noch mehr Aufgaben zur Berechnung des Break-Even-Points findest du hier:
Übungen zur Berechnung des Break-Even-Points
Die Kosten setzen sich zusammen aus den Fixkosten und den variablen Kosten. x sei die Stückzahl, die gefertigt wird. Dann lautet die zugehörige Funktionsgleichung f(x)=1,5x+200.
Die Funktionsgleichung für den Erlös lautet g(x)=4x
Erweiterung: Angebot und Nachfrage - Gleichgewichtspreis
Eine weitere Anwendung der Mathematik im Fach Sozialwissenschaften ist die Betrachtung von Angebot und Nachfrage auf dem Markt. Das Angebot sind alle Güter und Dienstleitungen, die erworben werden können. Die Nachfrage ist der Bedarf nach einem Produkt.
Hier findest du mehr Informationen zum Gleichgewichtspreis (Angebot und Nachfrage)
Gleichgewichtspreis