Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Addieren und Subtrahieren: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (47 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | |||
<br> | |||
[[Datei:Schullogo HLR.jpg|rechts|rahmenlos|80x80px]] | |||
{{Navigation|[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen| 0) Vorwissen]]<br> | |||
[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Addieren und Subtrahieren|1) Addieren und subtrahieren von Brüchen]]<br> | |||
[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Multiplizieren|2) Multiplizieren von Brüchen]]<br> | |||
[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Dividieren|3) Dividieren von Brüchen]]<br> | |||
[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Verbindung der Rechenarten| 4) Verbindung der Rechenarten]]<br> | |||
[[Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Bruchteile beliebiger Größen|5) Bruchteile beliebiger Größen]]}} | |||
==Addieren und Subtrahieren von Brüchen== | ==Addieren und Subtrahieren von Brüchen== | ||
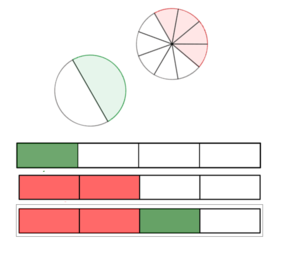
[[Datei:Rechnen mit Brüchen Einstieg.png|rahmenlos|300x300px]] | [[Datei:Rechnen mit Brüchen Einstieg.png|rahmenlos|300x300px]] | ||
| Zeile 10: | Zeile 20: | ||
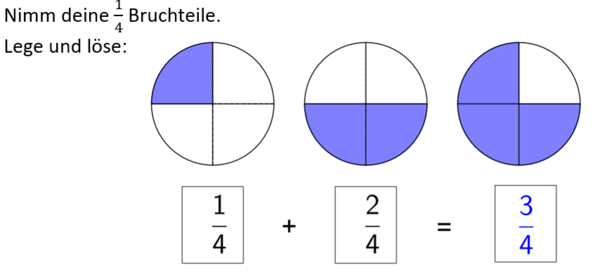
<div class="width-1-2">a) Lege und löse:<br> | <div class="width-1-2">a) Lege und löse:<br> | ||
<math>\tfrac{1}{4}</math> + <math>\tfrac{2}{4}</math> = ?</div> | <math>\tfrac{1}{4}</math> + <math>\tfrac{2}{4}</math> = ?</div> | ||
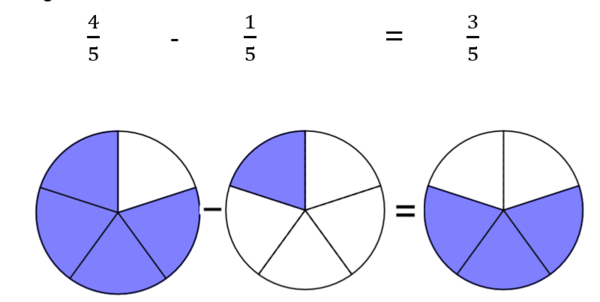
<div class="width-1-2">b) Lege und löse:<br><math>\tfrac{4}{5}</math> | <div class="width-1-2">b) Lege und löse:<br><math>\tfrac{4}{5}</math> - <math>\tfrac{1}{5}</math> = ?</div> | ||
</div> | </div> | ||
|3=Üben}} | |3=Üben}} | ||
| Zeile 26: | Zeile 36: | ||
Hier Fotos von Lösungen der Schüler sammeln und einfügen... | Hier Fotos von Lösungen der Schüler sammeln und einfügen... | ||
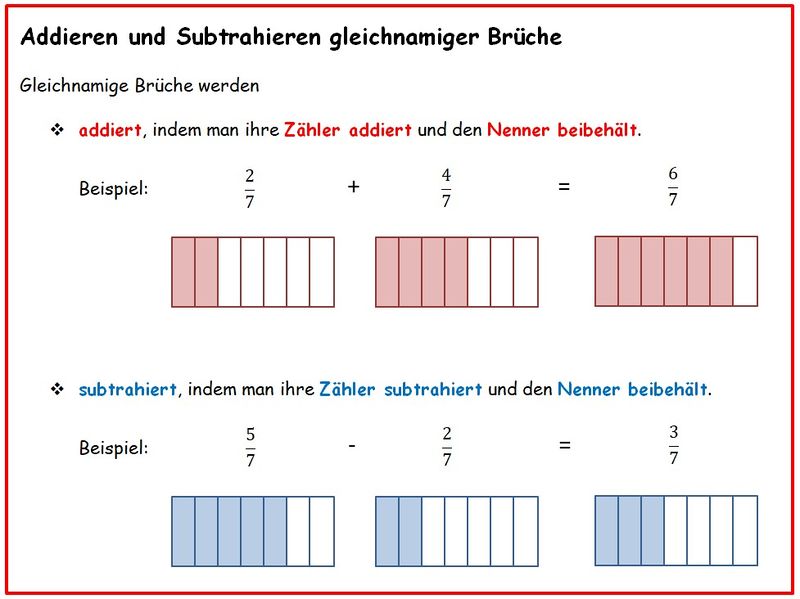
{{Box| | {{Box|Hefteintrag: Gleichnamige Brüche addieren und subtrahieren|[[Datei:Merkkasten - Addieren und Subtrahieren gleichnamiger Brüche.jpg|800x800px]]|Arbeitsmethode}} | ||
[[Datei: | |||
{{Lösung versteckt|1=Erinnerung: Brüche mit dem gleichen Nenner heißen "gleichnamig".<br> | {{Lösung versteckt|1=Erinnerung: Brüche mit dem gleichen Nenner heißen "gleichnamig".<br> | ||
[[Datei:Gleichnamige Brüche.png|rahmenlos]]|2=Erinnerung: Was heißt gleichnamig?|3=Schließen}} | [[Datei:Gleichnamige Brüche.png|rahmenlos|600x600px]]|2=Erinnerung: Was heißt gleichnamig?|3=Schließen}} | ||
{{#ev:youtube|bSoPRCfJMcg|800|center|||start=0&end=88}} | {{#ev:youtube|bSoPRCfJMcg|800|center|||start=0&end=88}} | ||
{{LearningApp|app=p1z84o6n519|width=100%|height=600px}} | {{LearningApp|app=p1z84o6n519|width=100%|height=600px}} | ||
| Zeile 46: | Zeile 56: | ||
{{Box|Übung 4 - Buch|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe in dein Heft und löse. | {{Box|Übung 4 - Buch|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe in dein Heft und löse. | ||
* S. | * S. 56 Nr. 2 (im Kopf) | ||
* S. 57 Nr. | * S. 57 Nr. 4 (im Kopf) | ||
* S. 57 Nr. | * S. 57 Nr. 5 (Kürze das Ergebnis!) | ||
* S. 57 Nr. 11 Schreibe das Ergebnis als gemischte Zahl! | * S. 57 Nr. 11 Schreibe das Ergebnis als gemischte Zahl! | ||
* S. 57 Nr. 12 Kürze das Ergebnis und schreibe es als gemischte Zahl! | * S. 57 Nr. 12 Kürze das Ergebnis und schreibe es als gemischte Zahl! | ||
* | |Üben}} | ||
{{Lösung versteckt|Tipps: | |||
* Achte auf die verschiedenen Rechenarten (+ oder -) | |||
* Prüfe zum Schluss, ob du das Ergebnis noch KÜRZEN kannst. | |||
* Kürze vollständig. | |||
* Prüfe, ob du das Ergebnis in die gemischte Schreibweise umwandeln kannst (wenn der Zähler größer ist als der Nenner)|Tipps zu den Aufgaben|Verbergen}} | |||
{{Box|1= Hefteintrag:Gleichnamige Brüche in gemischter Schreibweise addieren|2= | {{Box|1= Hefteintrag: Gleichnamige Brüche in gemischter Schreibweise addieren (subtrahieren)|2=Wandle die gemischte Zahl zuerst in einen unechten Bruch um: | ||
<div class="grid"> | <div class="grid"> | ||
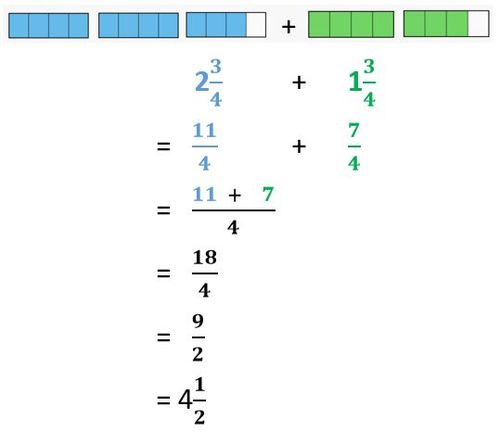
<div class="width-1-2">1 | <div class="width-1-2">Beispiel 1<br> | ||
<div class="width-1-2">2 | [[Datei:Gleichnamige Brüche in gemischter Schreibweise addieren Beispiel.jpg|rahmenlos|500x500px]] | ||
</div> | |||
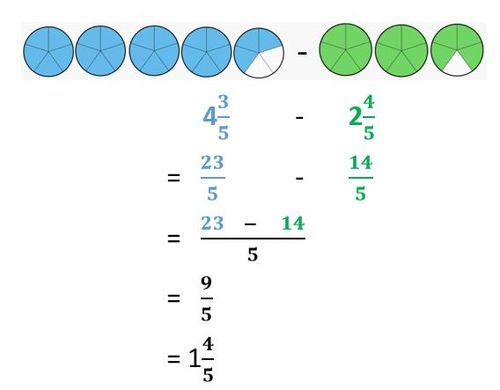
<div class="width-1-2">Beispiel 2<br> | |||
[[Datei:Gleichnamige Brüche in gemischter Schreibweise subtrahieren Beispiel.jpg|rahmenlos|500x500px]]</div> | |||
</div>|3=Arbeitsmethode}} | </div>|3=Arbeitsmethode}} | ||
| Zeile 76: | Zeile 94: | ||
{{Box|Übung 6|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe in dein Heft und löse schrittweise. | {{Box|Übung 6|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe in dein Heft und löse schrittweise. | ||
* S. 70 Nr. 4 (Vergleiche mit den Lösungen hinten im Buch.)|Üben}} | * S. 70 Nr. 4 (Vergleiche mit den Lösungen hinten im Buch.) | ||
* S. 57 Nr. 13|Üben}} | |||
===2 Addieren und Subtrahieren ungleichnamiger Brüche=== | ===2 Addieren und Subtrahieren ungleichnamiger Brüche=== | ||
| Zeile 85: | Zeile 103: | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">a) Lege und löse:<br> | <div class="width-1-2">a) Lege und löse:<br> | ||
<math>\tfrac{1}{4}</math> + <math>\tfrac{3}{8}</math> = ?</div> | <big><math>\tfrac{1}{4}</math> + <math>\tfrac{3}{8}</math> = ?</big></div> | ||
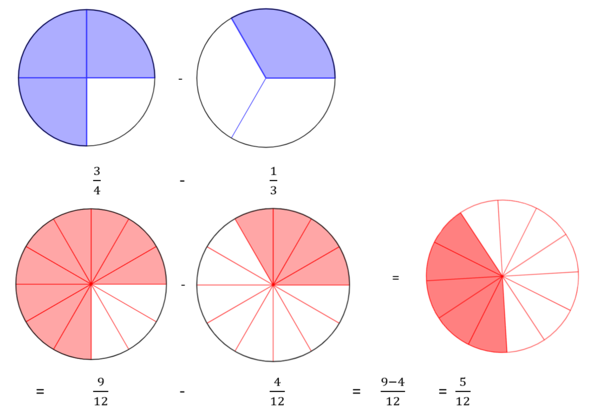
<div class="width-1-2">b) Lege und löse:<br><math>\tfrac{3}{4}</math> - <math>\tfrac{1}{3}</math> = ?</div> | <div class="width-1-2">b) Lege und löse:<br><big><math>\tfrac{3}{4}</math> - <math>\tfrac{1}{3}</math> = ?</big></div> | ||
</div> | </div> | ||
Welches Problem stellt sich?<br> | Welches Problem stellt sich?<br> | ||
Hast du eine Idee, wie du vorgehen kannst?|3=Üben}} | Hast du eine Idee, wie du vorgehen kannst?|3=Üben}} | ||
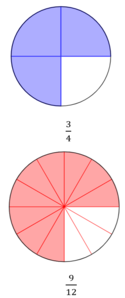
{{Lösung versteckt|Die Teile sind nicht gleich groß, die Brüche sind nicht gleichnamig. Kannst du statt der Viertel-Bruchteile den Bruch <math>\tfrac{1}{4}</math> auch mit anderen Bruchteilen legen?|Tipp 1|Schließen}} | <div class="grid"> | ||
<div class="width-1-2">{{Lösung versteckt|Die Teile sind nicht gleich groß, die Brüche sind nicht gleichnamig. Kannst du statt der Viertel-Bruchteile den Bruch <math>\tfrac{1}{4}</math> auch mit anderen Bruchteilen legen?|Tipp 1 zu a)|Schließen}} | |||
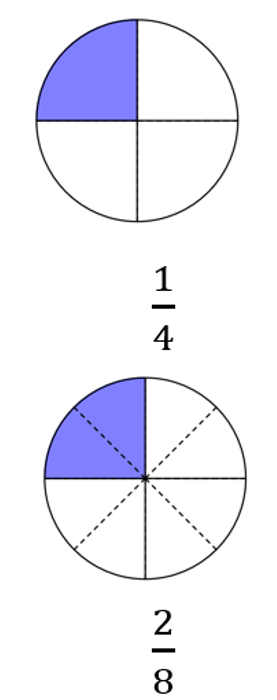
{{Lösung versteckt|Lege den Bruch <math>\tfrac{1}{4}</math> mit zwei Achtel-Teilen aus.<br> | {{Lösung versteckt|Lege den Bruch <math>\tfrac{1}{4}</math> mit zwei Achtel-Teilen aus.<br> | ||
[[Datei:Ein Viertel gleich zwei Achtel.png|rahmenlos]]|Tipp 2|Schließen}} | [[Datei:Ein Viertel gleich zwei Achtel.png|rahmenlos]]|Tipp 2 zu a)|Schließen}} | ||
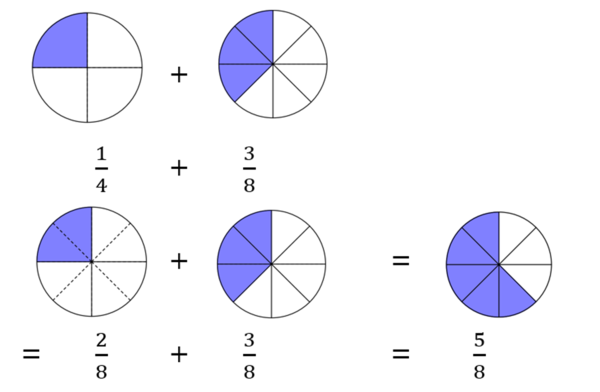
{{Lösung versteckt|[[Datei:Ein Viertel plus drei Achtel gleich fünf Achtel.png|rahmenlos|600x600px]]|Lösung|Schließen}} | {{Lösung versteckt|[[Datei:Ein Viertel plus drei Achtel gleich fünf Achtel.png|rahmenlos|600x600px]]|Lösung zu a)|Schließen}}</div> | ||
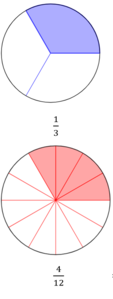
<div class="width-1-2">{{Lösung versteckt|Die Bruchteile sind nicht gleich groß. Welche Bruchteile kannst du für beide Brüche verwenden, um sie damit zu legen?|Tipp 1 zu b)|Schließen}} | |||
{{Lösung versteckt|Lege die Brüche <math>\tfrac{3}{4}</math> und <math>\tfrac{1}{3}</math> jweils mit zwölftel Bruchteilen aus.<br> | |||
[[Datei:Drei Viertel gleich neun Zwölftel.png|rahmenlos|300x300px]] [[Datei:Ein Drittel gleich vier Zwöftel.png|rahmenlos|300x300px]]|Tipp 2 zu b)|Schließen}} | |||
{{Lösung versteckt|[[Datei:Neun Zwöfltel minus vier Zölftel gleich fünf Zwölftel.png|rahmenlos|600x600px]]|Lösung zu b)|Schließen}}</div> | |||
</div> | |||
{{Lösung versteckt|1=Brüche erweitern anschaulich: | |||
https://www.geogebra.org/m/JaDPDygR | |||
<ggb_applet id="NFy934MF" width="1339" height="587" border="888888" /><br> | |||
Applet von 15abe<br> | |||
Brüche kürzen anschaulich: | |||
https://www.geogebra.org/m/XehPMB5x | |||
<ggb_applet id="KZQtdDUK" width="1339" height="587" border="888888" /><br> | |||
Applet von 15abe<br>|2=Erinnerung: Brüche erweitern und kürzen (anschaulich)|3=Schließen}} | |||
Originallink:https://www.geogebra.org/p/JrJfHYTVBf | |||
<ggb_applet id="uurtzsfe" width="997" height="550" border="888888" /> | |||
<small>Applet von B.Lachner</small> | |||
{{LearningApp|app=pd5z9kgat22|width=100%|height=800px}} | |||
{{#ev:youtube|T3vhkqQ9CUk|800|center}} | |||
{{Box|Hefteintrag: Ungleichnamige Brüche addieren und subtrahieren|[[Datei:Merkkasten - Addieren und Subtrahieren ungleichnamiger Brüche.jpg|800x800px]]|Arbeitsmethode}} | |||
{{Box|Übung 8|Löse die folgenden LeraningApps-Kollektion. Melde dich mit deiner Klasse und deinem Vornamen an (Beispiel: 6c Tina)|Üben}} | |||
{{LearningApp|app=po9v3t5vk22|width=100%|height=500px}} | |||
{{Box|Übung 9 Buch|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab, erweitere auf einen gemeinsamen Nenner und addiere (subtrahiere). | |||
* S. 59 Nr. 4 | |||
* S. 59 Nr. 5 | |||
* S. 59 Nr. 7 (Kürze das Ergebnis und wandle in die gemischte Schreibweise um.) | |||
* S. 59 Nr. 8 (Kürze das Ergebnis und wandle in die gemischte Schreibweise um.) | |||
* S. 59 Nr. 9|Üben}} | |||
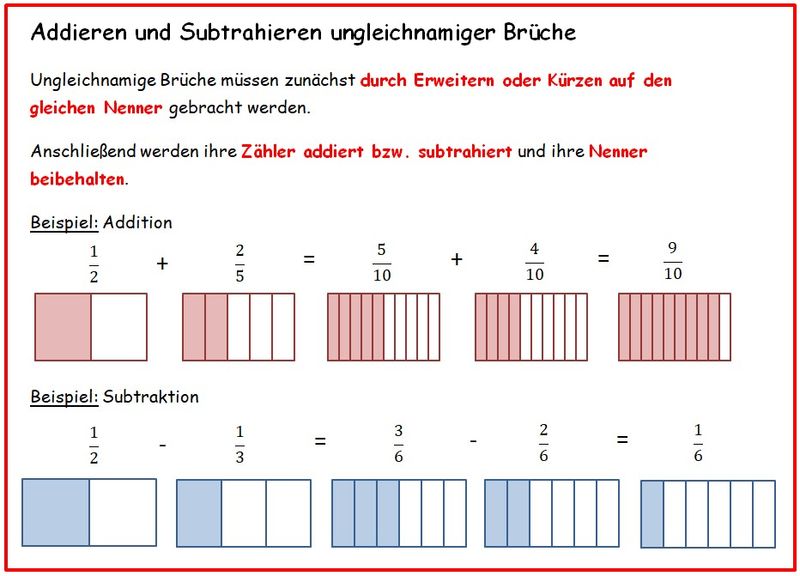
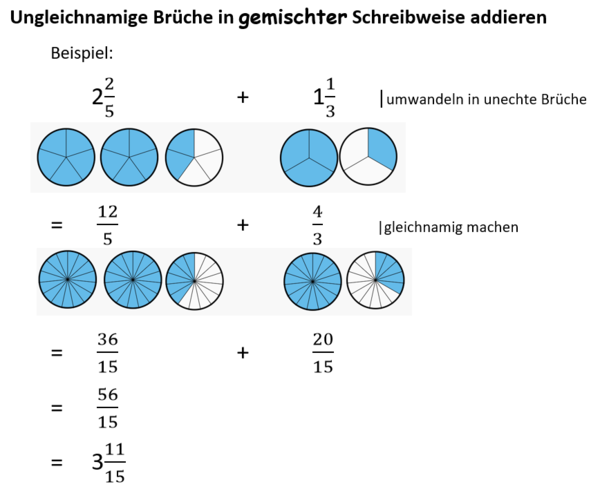
{{Box|1=Hefteintrag: Ungleichnamige Brüche in gemischter Schreibweise addieren (subtrahieren)|2=Wandle zunächst die Brüche in gemischter Schreibweise in unechte Brüche um. Dann rechnest du wie oben:<br> | |||
1. Umwandeln in die gemischte Schreibweise<br> | |||
2. Gleichnamig machen<br> | |||
3. Zähler addieren (subtrahieren), Nenner bleibt gleich<br> | |||
4. Das Ergebnis - falls möglich - kürzen und in die gemischte Schreibweise umwandeln.|3=Arbeitsmethode}} | |||
[[Datei:Ungleichnamige Brüche in gemischter Schreibweise addieren Beispiel.png|rahmenlos|600x600px]] | |||
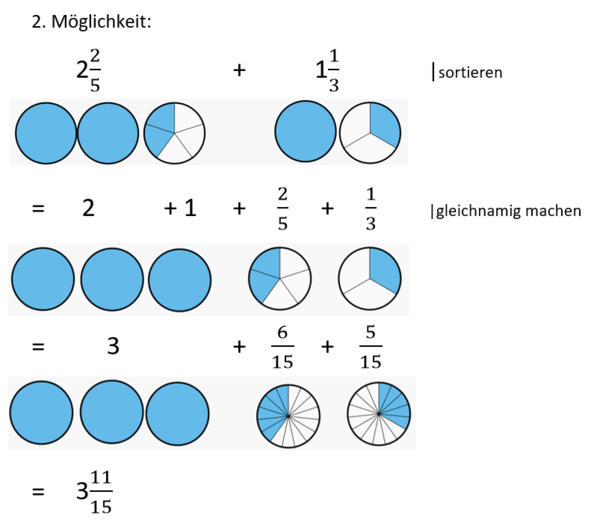
{{Lösung versteckt|[[Datei:Ungleichnamige Brüche in gemischter Schreibweise addieren 2. Möglichkeit.png|rahmenlos|600x600px]]|2. Möglichkeit|Verbergen}} | |||
{{LearningApp|app=pqppe7nfc20|width=100%|height=600px}} | |||
{{Lösung versteckt|1=Eine weitere Möglichkeit ungleichnamige Brüche in gemischter Schreibweise zu addieren besteht darin, zuerst die Ganzen zu addieren: | |||
{{LearningApp|app=pkdmmikzk22|width=100%|height=600px}}|2=Weitere Möglichkeit, ungleichnamige Brüche in gemischter Schreibweise zu addieren|3=Verbergen}} | |||
{{Box|Übung 10 Buch|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und löse schrittweise. | |||
*S. 60 Nr. 11 | |||
*S. 60 Nr. 12|Üben}} | |||
{{Lösung versteckt|1=a) 1<math>\tfrac{1}{2}</math> + <math>\tfrac{1}{4}</math> &mnsp;|umwandeln in einen unechten Bruch<br> | |||
= <math>\tfrac{3}{2}</math> + <math>\tfrac{1}{4}</math> |gleichnamig machen (HN 4)<br> | |||
= <math>\tfrac{6}{4}</math> + <math>\tfrac{1}{4}</math><br> | |||
... <br> | |||
Vergleiche deine Lösungen:<br> | |||
1<math>\tfrac{3}{4}</math>; 2<math>\tfrac{62}{63}</math>; 5<math>\tfrac{11}{15}</math>; 7<math>\tfrac{3}{35}</math>; 5<math>\tfrac{11}{30}</math>; 4<math>\tfrac{1}{63}</math>|2=Tipps, Lösungen zu Nr. 11|3=Verbergen}} | |||
{{Lösung versteckt|1=Vergleiche deine Lösungen:<br> | |||
2<math>\tfrac{1}{2}</math>; 10<math>\tfrac{4}{9}</math>; 1<math>\tfrac{3}{4}</math>; <math>\tfrac{4}{5}</math>; <math>\tfrac{19}{20}</math>; 1<math>\tfrac{11}{12}</math>|2=Lösungen zu Nr. 12|3=Verbergen}} | |||
{{Box|Übung 11 - ANTON|Nun bist du fit und kannst die Aufgaben zur Addition und Subtraktion bei [https://anton.app/de/ '''ANTON'''] lösen.|Üben}} | |||
{{Box|1=Übung 12 - freiwillige Übung|2=Bearbeite auf der Seite [https://www.matheaufgaben.net/mathe-online/?Aufgabentyp=Bruchrechnung Matheaufgabennet] weitere Aufgaben. Wähle dazu die Rechenarten Addieren oder Subtrahieren aus.|3=Üben}} | |||
{{Fortsetzung|weiter=2) Multiplizieren von Brüchen|weiterlink=Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Multiplizieren}} | |||
Rechnen mit Brüchen | |||
Aktuelle Version vom 22. Februar 2023, 14:12 Uhr
1) Addieren und subtrahieren von Brüchen
2) Multiplizieren von Brüchen
3) Dividieren von Brüchen
4) Verbindung der Rechenarten
Addieren und Subtrahieren von Brüchen
1 Addieren und subtrahieren gleichnamiger Brüche

Applet von GeoGebra Translation Team German
(direkter Link, falls die Darstellung schlecht ist: https://www.geogebra.org/m/mKDqMQAb )
Hier Fotos von Lösungen der Schüler sammeln und einfügen...
Tipps:
- Achte auf die verschiedenen Rechenarten (+ oder -)
- Prüfe zum Schluss, ob du das Ergebnis noch KÜRZEN kannst.
- Kürze vollständig.
- Prüfe, ob du das Ergebnis in die gemischte Schreibweise umwandeln kannst (wenn der Zähler größer ist als der Nenner)
2 Addieren und Subtrahieren ungleichnamiger Brüche
Brüche erweitern anschaulich: https://www.geogebra.org/m/JaDPDygR

Applet von 15abe
Brüche kürzen anschaulich:
https://www.geogebra.org/m/XehPMB5x

Applet von 15abe
Originallink:https://www.geogebra.org/p/JrJfHYTVBf

Applet von B.Lachner
Eine weitere Möglichkeit ungleichnamige Brüche in gemischter Schreibweise zu addieren besteht darin, zuerst die Ganzen zu addieren:
a) 1 + &mnsp;|umwandeln in einen unechten Bruch
= + |gleichnamig machen (HN 4)
= +
...
Vergleiche deine Lösungen:
Vergleiche deine Lösungen: