Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden konstruieren: Unterschied zwischen den Versionen
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
K (Lösung zu Aufgabe 1 als Tabelle formatiert) Markierung: Quelltext-Bearbeitung 2017 |
||
| (25 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 19: | Zeile 19: | ||
===Einführung=== | ===Einführung=== | ||
{{Box| | {{Box | Merksatz: Netz eines Körpers|2=Das Netz eines Körpers stellt diesen "auseinandergefaltet", also mit ausgebreiteten Flächen dar. Diese Darstellung erleichtert z.B. die Herstellung eines solchen Körpers aus Papier.|3=Merksatz | Farbe={{Farbe|grün|dunkel}}}} | ||
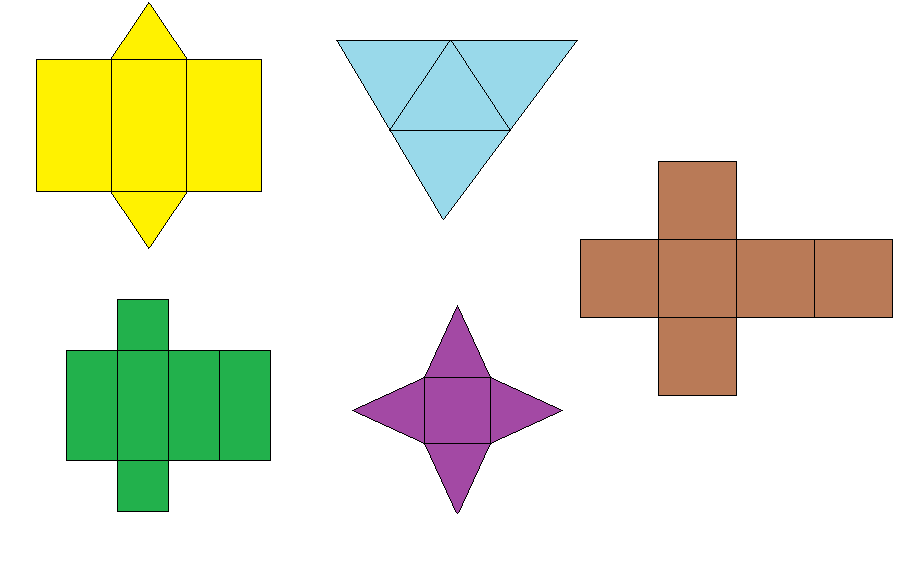
{{Box|Aufgabe 1: Zuordnung|Ordne den unten dargestellten Netzen die Körper zu, die daraus hergestellt werden können. | {{Box|Aufgabe 1: Zuordnung|Ordne den unten dargestellten Netzen die Körper zu, die daraus hergestellt werden können. | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Halte deine Ergebnisse auf dem Arbeitsblatt fest.''' | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Halte deine Ergebnisse auf dem Arbeitsblatt fest.''' | ||
{{Lösung versteckt|1=Mögliche Körper sind: Würfel, Zylinder, Tetraeder (Pyramide mit dreieckiger Grundfläche), Quader, Dreiecksprisma, Pyramide mit quadratischer Grundfläche, Kegel.|2=Tipp|3=Ausblenden}}[[Datei:Netze farbig.png|zentriert|gerahmt]] | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1=Mögliche Körper sind: Würfel, Zylinder, gleichseitiger Tetraeder (Pyramide mit dreieckiger Grundfläche), Quader, Dreiecksprisma, quadratische Pyramide (Pyramide mit quadratischer Grundfläche), Kegel.|2=Tipp|3=Ausblenden}} | ||
[[Datei:Netze farbig.png|zentriert|gerahmt]] | |||
{{Lösung versteckt|1={{(!}} class=wikitable | |||
! Farbe des Netzes | |||
! Daraus herstellbarer Körper | |||
{{!-}} | |||
{{!}} Gelb | |||
{{!}} Dreiecksprisma | |||
{{!-}} | |||
{{!}} Hellblau | |||
{{!}} (gleichseitiger) Tetraeder '''oder''' Pyramide mit dreieckiger Grundfläche | |||
{{!-}} | |||
{{!}} Grün | |||
{{!}} Quader | |||
{{!-}} | |||
{{!}} Lila | |||
{{!}} quadratische Pyramide '''oder''' Pyramide mit quadratischer Grundfläche | |||
{{!-}} | |||
{{!}} Braun | |||
{{!}} Würfel | |||
{{!)}}|2=Lösung|3=Ausblenden}}|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |||
===Netze entwerfen=== | ===Netze entwerfen=== | ||
| Zeile 41: | Zeile 64: | ||
Nicht alle Pyramiden haben eine quadratische Grundfläche. Ein Rechteck, ein Dreieck, ein Sechseck oder andere Vielecke als Grundfläche sind ebenfalls möglich. Ein besonderer Fall ist die Pyramide, die aus vier gleichseitigen Dreiecken besteht (womit die Grundfläche auch dreieckig ist). Dieser Körper heißt ''regelmäßiger Tetraeder''. | Nicht alle Pyramiden haben eine quadratische Grundfläche. Ein Rechteck, ein Dreieck, ein Sechseck oder andere Vielecke als Grundfläche sind ebenfalls möglich. Ein besonderer Fall ist die Pyramide, die aus vier gleichseitigen Dreiecken besteht (womit die Grundfläche auch dreieckig ist). Dieser Körper heißt ''regelmäßiger Tetraeder''. | ||
{{Box| | {{Box| Merksatz: Regelmäßiger Tetraeder|2=Ein regelmäßiger Tetraeder ist eine Pyramide, die aus vier gleichseitigen Dreiecken besteht (gleichseitige Dreiecke sind auch gleichwinklig; alle drei Innenwinkel betragen jeweils <math>60^{\circ}</math>). | ||
[[Datei:Triangular Pyramid (Tetrahedron).svg|mittig|zentriert|Schrägbild eines Tetraeders]]|3=Merksatz}} | [[Datei:Triangular Pyramid (Tetrahedron).svg|mittig|zentriert|Schrägbild eines Tetraeders]]|3=Merksatz | Farbe={{Farbe|grün|dunkel}}}} | ||
{{Box|Aufgabe 3: Netz eines | {{Box|Aufgabe 3: Netz eines regelmäßigen Tetraeders|Zeichne nun das Netz eines regelmäßigen Tetraeders. | ||
{{Lösung versteckt|1=Wie sehen alle Flächen eines regelmäßigen Tetraeders aus?|2=Tipp|3=Ausblenden}} | {{Lösung versteckt|1=Wie sehen alle Flächen eines regelmäßigen Tetraeders aus?|2=Tipp|3=Ausblenden}} | ||
{{Lösung versteckt|1=Deine Zeichnung sollte dem hellblauen Netz im Bild der Aufgabe 1 ähnlich sein.|2=Lösung|3=Ausblenden}} | {{Lösung versteckt|1=Deine Zeichnung sollte dem hellblauen Netz im Bild der Aufgabe 1 ähnlich sein.|2=Lösung|3=Ausblenden}} | ||
| Zeile 54: | Zeile 77: | ||
{{Box|Aufgabe 4: Vom Netz zum Körper| | {{Box|Aufgabe 4: Vom Netz zum Körper| | ||
'''a)''' Bewege den Schieberegler, um die Seitenflächen | '''a)''' Bewege den Schieberegler, um die Seitenflächen der Pyramide aufzurichten oder abzusenken. Durch Verschieben der Eckpunkte kannst du die Gestalt der Pyramide verändern. | ||
<ggb_applet id="Jhc3FeP8" width="1000" height="733" /> | <ggb_applet id="Jhc3FeP8" width="1000" height="733" /> | ||
'''b)''' Stelle aus dem in Aufgabe | '''b)''' Stelle aus dem in Aufgabe 2 angefertigten Netz eine Pyramide mit quadratischer Grundfläche her. Fixiere die Mantelfläche mit Klebeband, um zu verhindern, dass sich die Pyramide wieder "öffnet". | ||
|Arbeitsmethode|Farbe={{Farbe|orange}}}} | |Arbeitsmethode|Farbe={{Farbe|orange}}}} | ||
| Zeile 72: | Zeile 95: | ||
[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Bearbeite diese Aufgabe wieder auf dem Arbeitsblatt.''' | [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Bearbeite diese Aufgabe wieder auf dem Arbeitsblatt.''' | ||
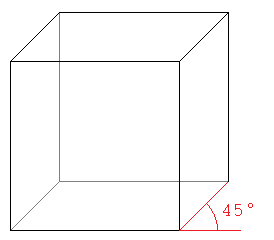
Zeichne das Schrägbild einer Pyramide mit quadratischer Grundfläche mit Grundflächenkantenlänge <math>a = 5</math> cm und Körperhöhe <math> | Zeichne das Schrägbild einer Pyramide mit quadratischer Grundfläche mit Grundflächenkantenlänge <math>a = 5</math> cm und Körperhöhe <math>h = 6</math> cm, indem du wie folgt vorgehst: | ||
# Zeichne zuerst die Grundfläche. Stell dir vor, die Grundfläche würde "nach hinten weggehen". Diese perspektivische Darstellung gelingt dir, indem du die "nach hinten weggehenden" Kanten | # Zeichne zuerst die Grundfläche. Stell dir vor, die Grundfläche würde "nach hinten weggehen". Diese perspektivische Darstellung gelingt dir, indem du die "nach hinten weggehenden" Kanten | ||
| Zeile 79: | Zeile 102: | ||
# Vervollständige das Schrägbild. Zeichne dazu die Diagonalen als Hilfslinien ein. Zeichne die Höhe der Pyramide ein. Verbinde die Spitze mit den Eckpunkten der Grundfläche. | # Vervollständige das Schrägbild. Zeichne dazu die Diagonalen als Hilfslinien ein. Zeichne die Höhe der Pyramide ein. Verbinde die Spitze mit den Eckpunkten der Grundfläche. | ||
{{Lösung versteckt|1=Die in die Tiefe, also nach hinten gehenden Seiten werden unter einem <math>45^{\circ}</math> Winkel gezeichnet; nicht sichtbare Kanten werden gestrichelt dargestellt | {{Lösung versteckt|1=Die in die Tiefe, also nach hinten gehenden Seiten werden unter einem <math>45^{\circ}</math> Winkel gezeichnet; nicht sichtbare Kanten werden gestrichelt dargestellt. | ||
<div style="width:calc(100% - 1rem); height:0; padding-bottom:62.2%;"><ggb_applet id="Z57aCNpm" width="1000" height="622"/></div> | <div style="width:calc(100% - 1rem); height:0; padding-bottom:62.2%;"><ggb_applet id="Z57aCNpm" width="1000" height="622"/></div> | ||
|2=Tipp|3=Tipp verbergen}} | Arbeitsmethode | Farbe={{Farbe|orange}} }} | |2=Tipp|3=Tipp verbergen}} | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
====Schrägbild eines Tetraeders==== | ====Schrägbild eines regelmäßigen Tetraeders==== | ||
{{Box | Aufgabe 6: Schrägbild eines Tetraeders | | {{Box | Aufgabe 6: Schrägbild eines Tetraeders | | ||
Zeichne das Schrägbild eines Tetraeders. Die Kanten der Grundfläche sind <math>4</math> cm lang und die Höhe der Pyramide soll <math>6</math> cm betragen. Beachte beim Zeichnen die Merkmale dieser besonderen Pyramide. | Zeichne das Schrägbild eines regelmäßigen Tetraeders. Die Kanten der Grundfläche sind <math>4</math> cm lang und die Höhe der Pyramide soll <math>6</math> cm betragen. Beachte beim Zeichnen die Merkmale dieser besonderen Pyramide. | ||
{{Lösung versteckt|1=Fertige dir eine Hilfszeichnung an mit deiner Grundfläche an, um die passende Verzerrung des Schrägbildes zu ermitteln. Tipp: Die Grundfläche ist gleichwinklig. | {{Lösung versteckt|1=Fertige dir eine Hilfszeichnung an mit deiner Grundfläche an, um die passende Verzerrung des Schrägbildes zu ermitteln. Tipp: Die Grundfläche ist gleichwinklig. | ||
| Zeile 92: | Zeile 115: | ||
{{Lösung versteckt|1=Wenn du weitere Hilfestellung benötigst, schaue dir dieses Video bis zur <math>4.</math> Minute an. [https://www.youtube.com/watch?v=HmXIOIdtDU8] | {{Lösung versteckt|1=Wenn du weitere Hilfestellung benötigst, schaue dir dieses Video bis zur <math>4.</math> Minute an. [https://www.youtube.com/watch?v=HmXIOIdtDU8] | ||
Hinweis: Es gibt auch die Möglichkeit, die Grundfläche mit Hilfe von Winkelmessungen anstatt mit dem Zirkel zu zeichnen, da die Grundfläche gleichwinklig ist und somit alle Winkel <math> | Hinweis: Es gibt auch die Möglichkeit, die Grundfläche mit Hilfe von Winkelmessungen anstatt mit dem Zirkel zu zeichnen, da die Grundfläche gleichwinklig ist und somit alle Winkel <math>60^{\circ}</math> betragen.|2=Tipp 2|3=Tipp 2 verbergen}} | ||
{{Lösung versteckt|1=Du kannst dir folgendes Video zum Vergleich deiner Lösung ansehen (ab Minute <math>4</math>): [https://www.youtube.com/watch?v=HmXIOIdtDU8]|2=Lösung|3=Lösung verbergen}} | Arbeitsmethode}} | {{Lösung versteckt|1=Du kannst dir folgendes Video zum Vergleich deiner Lösung ansehen (ab Minute <math>4</math>): [https://www.youtube.com/watch?v=HmXIOIdtDU8]|2=Lösung|3=Lösung verbergen}} | Arbeitsmethode}} | ||
| Zeile 100: | Zeile 123: | ||
====Lückentext==== | ====Lückentext==== | ||
{{Box | Aufgabe 7: Lückentext Pyramiden | | {{Box | Aufgabe 7: Lückentext Pyramiden | | ||
Vervollständige den | '''a)''' Vervollständige den Lückentext. | ||
Folgende Begriffe kannst du einsetzen: | Folgende Begriffe kannst du einsetzen: | ||
dreidimensional; halb so lang; beliebig viele Ecken; <math>90^{\circ}</math>; unverzerrt; gleichseitig; <math>45^{\circ}</math>; Tetraeder; Körper; Schrägbild; zweidimensional; Quader; Verzerrungswinkel; <math>60^{\circ}</math>; doppelt so groß; verzerrt | ''dreidimensional; halb so lang; beliebig viele Ecken; <math>90^{\circ}</math>; unverzerrt; gleichseitig; <math>45^{\circ}</math>; Tetraeder; Körper; Schrägbild; zweidimensional; Quader; Verzerrungswinkel; <math>60^{\circ}</math>; doppelt so groß; verzerrt; rechter Winkel'' | ||
{{LearningApp|width=100%|height=330px|app=27548524}} | |||
'''b)''' [[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''Übertrage die richtige Lösung auf dein Arbeitsblatt.''' | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | |||
====Praktische Sicherung==== | ====Praktische Sicherung==== | ||
{{Box | Aufgabe 8: Auf dem Dach | | {{Box | Aufgabe 8: Auf dem Dach | | ||
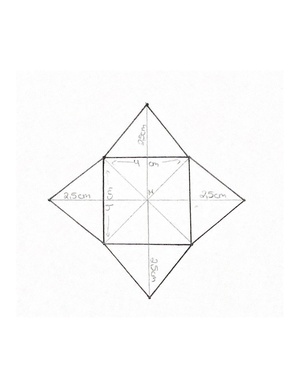
Eine Scheune ist <math>40</math> m lang und ebenso breit. Sie hat ein pyramidenförmiges, <math>15</math> m hohes Dach. Die Seitenflächen dieses Dachs haben eine Seitenflächenhöhe von <math>25</math> m. | |||
'''a)''' Zeichne das Netz des Daches im Maßstab <math>1:1000</math>. | |||
{{Lösung versteckt|1=Im Maßstab <math>1:1000</math> entsprechen <math>10</math> m in der Realität <math>1</math> cm in deiner Skizze.|2=Tipp zu a)|3=Tipp verbergen}} | |||
{{Lösung versteckt|1=Folgende Skizze zeigt eine mögliche Lösung. | |||
[[Datei:Netz Scheunendach.pdf|zentriert|mini]]|2=Lösung zu a)|3=Lösung verbergen}} | |||
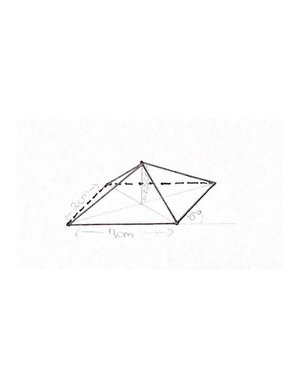
'''b)''' Zeichne ein maßstabsgetreues Schrägbild des Scheunendaches im Maßstab <math>1:1000</math>. | |||
{{Lösung versteckt|1= | {{Lösung versteckt|1=Achte beim Vergleich mit deiner Lösung darauf, ob... | ||
# du die nicht sichtbaren Linien gestrichelt eingezeichnet hast. | |||
# dein Verzerrungswinkel <math>45^{\circ}</math> beträgt. | |||
[[Datei:Schrägbild Scheunendach.pdf|zentriert|mini]]|2=Lösung zu b)|3=Lösung verbergen}} | |||
| Arbeitsmethode | Farbe=#CD2990 }} | | Arbeitsmethode | Farbe=#CD2990 }} | ||
Aktuelle Version vom 1. Dezember 2022, 07:46 Uhr
Rückblick und Motivation
Pyramiden begegnen uns nicht nur im Mathematikunterricht, sondern auch in der realen Welt, wie z.B. in Architektur (Bild rechts) und Bauingenieurwesen (Konstruktion und Betrieb von Bauwerken des Hoch-, Verkehrs-, Tief- und Wasserbaus). Du kannst bereits Pyramiden im Alltag erkennen und Beispiele dafür nennen.
Einführung
Netze entwerfen
Netz einer Pyramide mit quadratischer Grundfläche zeichnen
Der regelmäßige Tetraeder
Nicht alle Pyramiden haben eine quadratische Grundfläche. Ein Rechteck, ein Dreieck, ein Sechseck oder andere Vielecke als Grundfläche sind ebenfalls möglich. Ein besonderer Fall ist die Pyramide, die aus vier gleichseitigen Dreiecken besteht (womit die Grundfläche auch dreieckig ist). Dieser Körper heißt regelmäßiger Tetraeder.
Körper herstellen
Vom Netz zum Körper
Eben hast du (mindestens) ein Körpernetz gezeichnet. Nun soll daraus ein dreidimensionaler Körper hergestellt werden. Nachfolgend ist die Herstellung einer Pyramide dargestellt.