Digitale Werkzeuge in der Schule/Pyramiden entdecken/Pyramiden verknüpfen: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 66: | Zeile 66: | ||
|Aufgabe 2: Sightseeing in Paris 1 - Der Louvre | |Aufgabe 2: Sightseeing in Paris 1 - Der Louvre | ||
|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
[[Datei:Parigi - Pyramide du Louvre - panoramio.jpg|mini|Glaspyramide im Innenhof des Louvre.]] Du machst mit deiner Familie Urlaub in Paris und besichtigst einige Sehenswürdigkeiten. Zuerst nehmt ihr an einer Führung durch das berühmte Museum ''Louvre'' teil. Das nebenstehende Bild zeigt die im Innenhof des Louvre stehende Glaspyramide mit quadratischer Grundfläche. | |||
Du machst mit deiner Familie Urlaub in Paris und besichtigst einige Sehenswürdigkeiten. Zuerst nehmt ihr an einer Führung durch das berühmte Museum ''Louvre'' teil. Das nebenstehende Bild zeigt die im Innenhof des Louvre stehende Glaspyramide mit quadratischer Grundfläche. | |||
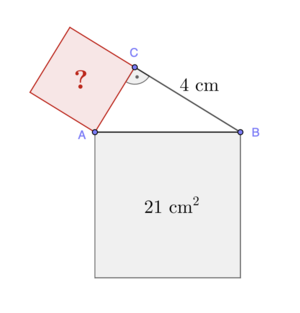
Während eurer Führung durch das Museum stellt eine Touristin folgende Frage: "Wie lang sind die Edelstahlträger an den Seitenkanten der Pyramide?" Der Touristenführer weiß nur, dass die Pyramide 21 Meter hoch ist. | Während eurer Führung durch das Museum stellt eine Touristin folgende Frage: "Wie lang sind die Edelstahlträger an den Seitenkanten der Pyramide?" Der Touristenführer weiß nur, dass die Pyramide 21 Meter hoch ist. | ||
| Zeile 161: | Zeile 159: | ||
|Arbeitsmethode}} | |Arbeitsmethode}} | ||
{{Box|1=Checkliste zur Bestimmung der Mantelfläche|2= | {{Box|1=|Aufgabe 3: Checkliste zur Bestimmung der Mantelfläche|2= | ||
In Aufgabe 2 hast du bereits eine Möglichkeit zur Bestimmung der Mantelfläche einer Pyramide erkundet und in Aufgabenteil 2d) auch schon angefangen, die dazu nötige Vorgehensweise zu beschreiben. | In Aufgabe 2 hast du bereits eine Möglichkeit zur Bestimmung der Mantelfläche einer Pyramide erkundet und in Aufgabenteil 2d) auch schon angefangen, die dazu nötige Vorgehensweise zu beschreiben. | ||
| Zeile 171: | Zeile 169: | ||
Übertrage die Checkliste auf das Arbeitsblatt "Pyramiden verknüpfen". | Übertrage die Checkliste auf das Arbeitsblatt "Pyramiden verknüpfen". | ||
|3= | |3=Arbeitsmethode}} | ||
{{Box | {{Box | ||
|Aufgabe | |1=Aufgabe 4 ⭐: Sightseeing in Paris 2 - Der Eiffelturm | ||
|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |2=[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
[[Datei:Tour Eiffel Wikimedia Commons.jpg|120px|mini|Eiffelturm]] | [[Datei:Tour Eiffel Wikimedia Commons.jpg|120px|mini|Eiffelturm]] | ||
| Zeile 191: | Zeile 189: | ||
|2=Tipp 2 anzeigen |3= Tipp 2 verbergen}} | |2=Tipp 2 anzeigen |3= Tipp 2 verbergen}} | ||
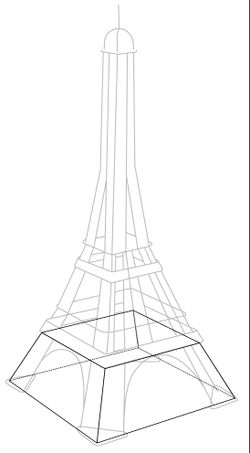
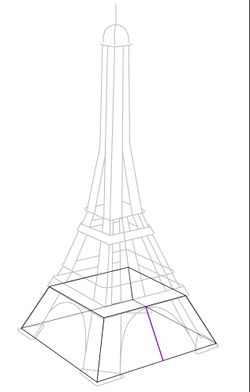
{{Lösung versteckt|1= Der Eiffelturm besitzt bis zur 1. Etage die Form eines Pyramidenstumpfes. Den Pyramidenstumpf | {{Lösung versteckt|1= Der Eiffelturm besitzt bis zur 1. Etage die Form eines Pyramidenstumpfes. Den Pyramidenstumpf kannst du der unten stehenden Skizze entnehmen. Überlege dir anhand der Skizze welche Größen du schon kennst und welche Größen du noch bestimmen musst. | ||
[[Datei:Eiffelturm mit Pyramidenstumpf.jpg| zentriert | rahmenlos | 250px | thumb]] | [[Datei:Eiffelturm mit Pyramidenstumpf.jpg| zentriert | rahmenlos | 250px | thumb]] | ||
|2=Tipp 3 anzeigen |3= Tipp 3 verbergen}} | |2=Tipp 3 anzeigen |3= Tipp 3 verbergen}} | ||
| Zeile 209: | Zeile 207: | ||
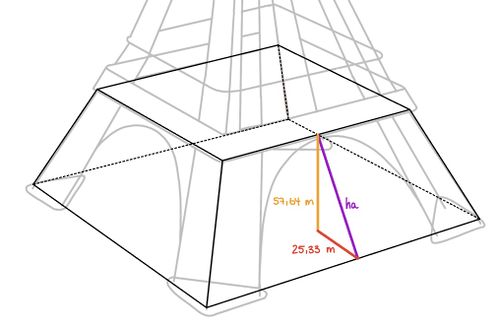
[[Datei:Eiffelturm mit Pyramidenstumpf und Hilfsdreieck.jpg|zentriert | rahmenlos | 500px | thumb]] | [[Datei:Eiffelturm mit Pyramidenstumpf und Hilfsdreieck.jpg|zentriert | rahmenlos | 500px | thumb]] | ||
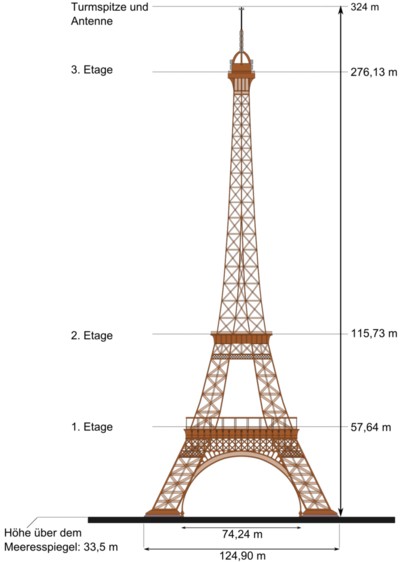
Die Breite der ersten Etage kann anhand der Breite des Torbogens auf <math>74{,}24 ~\text{m}</math> geschätzt werden. Die Länge eines Fußes des Eiffelturms wird über die folgende Gleichung bestimmt: | Die Breite der ersten Etage kann anhand der Breite des Torbogens auf <math>74{,}24 ~\text{m}</math> geschätzt werden. Die <span style="color:darkred">'''Länge eines Fußes'''</span> des Eiffelturms wird über die folgende Gleichung bestimmt: | ||
<math>\text{ | <math>l_\text{Fuß} = \frac{124{,}90 ~\text{m} - 74{,}24 ~\text{m}}{2} = 25{,}33 ~\text{m}</math>. | ||
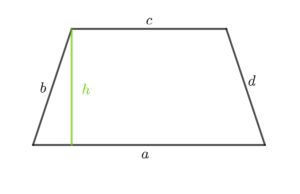
Die Seitenhöhe <math>h_a</math> des Trapezes wird über den Satz des Pythagoras bestimmt. Es gilt: | Die Seitenhöhe <math>h_a</math> des Trapezes wird über den Satz des Pythagoras bestimmt. Es gilt: | ||
| Zeile 240: | Zeile 238: | ||
{{Box | {{Box | ||
|Aufgabe | |1=Aufgabe 5 ⭐: Der Würfel | ||
|[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | |2=[[Datei:Grundlagen-bearbeiten.png|30px|middle]] '''zurück zum Arbeitsblatt''' | ||
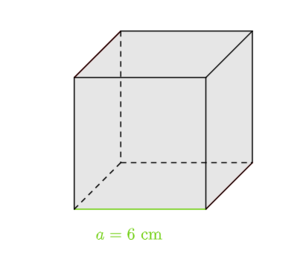
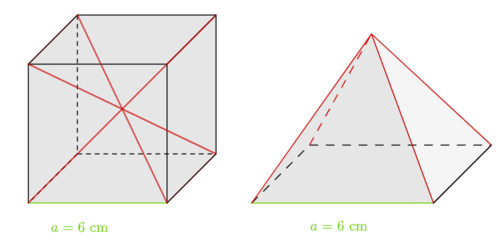
Der unten abgebildete Würfel lässt sich aus 6 regelmäßigen, gleichartigen Pyramiden zusammensetzen. | Der unten abgebildete Würfel lässt sich aus 6 regelmäßigen, gleichartigen Pyramiden zusammensetzen. | ||
| Zeile 257: | Zeile 255: | ||
Kannst du dir nun besser vorstellen, wie die gesuchte Pyramide aussieht? | Kannst du dir nun besser vorstellen, wie die gesuchte Pyramide aussieht? | ||
<div style="width:calc(100% - 1rem); height:0; padding-bottom:50%;"><ggb_applet id="utuufrpf" width=" | <div style="width:calc(100% - 1rem); height:0; padding-bottom:50%;"><ggb_applet id="utuufrpf" width="1000" height="500"/></div> | ||
|2=Tipp 3 zu a) anzeigen|3= Tipp 3 zu a) verbergen}} | |2=Tipp 3 zu a) anzeigen|3= Tipp 3 zu a) verbergen}} | ||
| Zeile 289: | Zeile 287: | ||
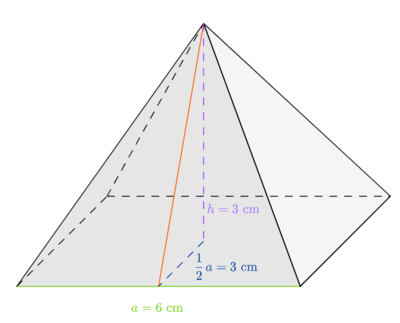
Mit Hilfe des Satzes des Pythagoras ergibt sich die folgende Formel: | Mit Hilfe des Satzes des Pythagoras ergibt sich die folgende Formel: | ||
<math> (h_a)^2=h^2+\biggl(\frac{1}{2}\cdot a\biggr)^2 </math>. | <math> (h_a)^{2}=h^2+\biggl(\frac{1}{2}\cdot a\biggr)^2 </math>. | ||
Setzen wir nun, die uns bekannten Werte für <math> h </math> und <math> a </math> ein, so erhalten wir: | Setzen wir nun, die uns bekannten Werte für <math> h </math> und <math> a </math> ein, so erhalten wir: | ||