|
|
| Zeile 115: |
Zeile 115: |
| |3=Kurzinfo}} | | |3=Kurzinfo}} |
|
| |
|
| {{Box|1=Aufgabe 4: Zuordnung von Dreiecksarten|2= | | {{Box|1=Aufgabe 5: Zuordnung von Dreiecksarten|2= |
| Entscheide, ob es sich bei dem gezeigten Dreieck um ein gleichschenkliges Dreieck, ein gleichseitiges Dreieck, ein rechtwinkliges Dreieck oder ein allgemeines Dreieck handelt. | | Entscheide, ob es sich bei dem gezeigten Dreieck um ein gleichschenkliges Dreieck, ein gleichseitiges Dreieck, ein rechtwinkliges Dreieck oder ein allgemeines Dreieck handelt. |
|
| |
|
| Zeile 125: |
Zeile 125: |
|
| |
|
|
| |
|
| {{Box|1=Aufgabe 4: Dreieckstypen untersuchen |2=Die Seite AB des Dreiecks ABC ist fix und hat die Länge 8, der Punkt C lässt sich bewegen. Untersuche durch das Verschieben des Punktes C die verschiedenen Dreiecksarten und setze dabei möglichst viele farbige Punkte für die verschiedenen Dreiecksarten. | | {{Box|1=Aufgabe 5: Dreieckstypen untersuchen |2=Die Seite AB des Dreiecks ABC ist fix und hat die Länge 8, der Punkt C lässt sich bewegen. Untersuche durch das Verschieben des Punktes C die verschiedenen Dreiecksarten und setze dabei möglichst viele farbige Punkte für die verschiedenen Dreiecksarten. |
| Stelle eine Vermutung auf, wo du welche Dreiecksarten finden kannst. | | Stelle eine Vermutung auf, wo du welche Dreiecksarten finden kannst. |
|
| |
|
| Zeile 132: |
Zeile 132: |
| |3=Arbeitsmethode |Farbe=#CD2990}} | | |3=Arbeitsmethode |Farbe=#CD2990}} |
|
| |
|
| {{Box|1=Aufgabe 4: Eigenschaften von Dreiecken|2= | | {{Box|1=Aufgabe 5: Eigenschaften von Dreiecken|2= |
|
| |
|
| Gib an, ob die folgenden Aussagen wahr oder falsch sind. Begründe deine Überlegung z.B. mit einer Zeichnung. | | Gib an, ob die folgenden Aussagen wahr oder falsch sind. Begründe deine Überlegung z.B. mit einer Zeichnung. |
Version vom 19. Mai 2022, 17:02 Uhr
Info
In diesem Lernpfadkapitel entdeckst du, wie du Dreiecke vergleichen kannst. Dabei lernst du die verschiedenen Dreiecksarten kennen.
Bei den Aufgaben unterscheiden wir folgende Typen:
- In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
- Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
- Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.
Erkundung von Dreiecken
Aufgabe 1: Erkundung von Dreiecken
 zurück zum Arbeitsblatt
zurück zum Arbeitsblatt
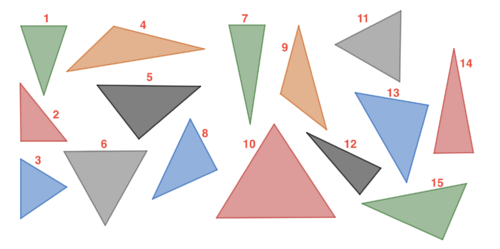
In der Abbildung siehst du verschiedene Dreiecke.
Tim hat bei den Dreiecken schon eine Gemeinsamkeit entdeckt. Findest du weitere?
Gib Dreiecke an die Gemeinsamkeiten haben und beschreibe diese Gemeinsamkeiten in wenigen Sätzen auf deinem Arbeitsblatt.
 Hinweis: Du findest die Dreiecke auch auf deinem Arbeitsblatt in vergrößerter Form.
Hinweis: Du findest die Dreiecke auch auf deinem Arbeitsblatt in vergrößerter Form.
Du kannst Dreiecke vergleichen, indem du ihre Winkel oder ihre Seitenlängen vergleichst.
Charakterisierungen von Dreiecken

Unterscheidung von Dreiecken mit Winkeln
Aufgabe 2: Unterscheidung von Dreiecken mithilfe von Winkeln
Tim stellt hier eine spannende Vermutung auf! Finde durch Verschieben des Punktes heraus, ob Tim Recht hat. Begründe deine Antwort auf dem Arbeitsblatt.
 zurück zum Arbeitsblatt
zurück zum Arbeitsblatt

Merksatz: Unterscheidung von Dreiecken mithilfe von Winkeln
Vervollständige den Merksatz. (Hinweis: Wenn du dir unsicher bist, verschiebe in Aufgabe 3 noch einmal den Punkt und schau dir die Winkel genauer an)
Ein spitzwinkliges Dreieck hat drei spitze Winkel (<90°).
Ein stumpfwinkliges Dreieck hat einen stumpfen Winkel (>90°) und zwei spitze Winkel.
Ein rechtwinkliges Dreieck hat einen rechten Winkel (genau 90°) und zwei spitze Winkel.
Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt und beschrifte die abgebildeten Dreiecke.
 zurück zum Arbeitsblatt
zurück zum Arbeitsblatt
Unterscheidung von Dreiecken mit Seitenlängen
Aufgabe 3: Unterscheidung von Dreiecken mithilfe von Seiten

Überlege wie die Dreiecke heißen könnten, wenn du zwischen einem Dreieck mit zwei gleichlangen Seiten und einem Dreieck mit drei gleichlangen Seiten unterscheiden möchtest.
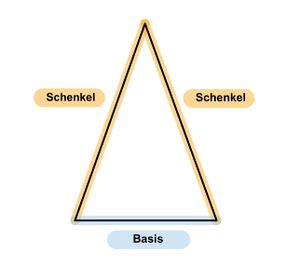
Erinnerst du dich noch an die Fachbegriffe "Basis" und "Schenkel" eines Dreiecks?
Merksatz: Unterscheidung von Dreiecken mithilfe von Seitenlängen
Vervollständige den Merksatz.
Hat ein Dreieck zwei gleich lange Seiten, nennt man es auch gleichschenkliges Dreieck. Sind alle Seiten gleich lang heißt das Dreieck gleichseitiges Dreieck.
Wenn du alle Lücken richtig ausgefüllt hast, schreibe den Merksatz auf dein Arbeitsblatt und beschrifte die abgebildeten Dreiecke.
 zurück zum Arbeitsblatt
zurück zum Arbeitsblatt
Aufgabe 4: Unterscheidung von Dreiecken mithilfe der Seitenlängen
Ordne den Bildern einen richtigen Zettel zu, indem du die verschiedenen Dreiecke zählst.
 Hinweis: Klicke auf die Bilder um die Abbildungen größer zu sehen.
Hinweis: Klicke auf die Bilder um die Abbildungen größer zu sehen.
Weiterführende Aufgaben
Info
Du hast nun gelernt, wie man Dreiecke mithilfe von Winkeln und Seitenlängen unterscheiden kann. Die folgenden Aufgaben kombinieren nun diese beiden Unterscheidungen.
Die folgenden Aufgaben haben unterschiedliche Schwierigkeitsgrade. Du kannst frei entscheiden, welche der Aufgaben du bearbeiten möchtest.
Aufgabe 5: Zuordnung von Dreiecksarten
Entscheide, ob es sich bei dem gezeigten Dreieck um ein gleichschenkliges Dreieck, ein gleichseitiges Dreieck, ein rechtwinkliges Dreieck oder ein allgemeines Dreieck handelt.
Wenn du dir unsicher bist, schaue die Bezeichnungen noch einmal im Merksatz nach.
 Hinweis: Es können mehrere Antworten richtig sein.
Hinweis: Es können mehrere Antworten richtig sein.
Aufgabe 5: Dreieckstypen untersuchen
Die Seite AB des Dreiecks ABC ist fix und hat die Länge 8, der Punkt C lässt sich bewegen. Untersuche durch das Verschieben des Punktes C die verschiedenen Dreiecksarten und setze dabei möglichst viele farbige Punkte für die verschiedenen Dreiecksarten.
Stelle eine Vermutung auf, wo du welche Dreiecksarten finden kannst.
Aufgabe 5: Eigenschaften von Dreiecken
Gib an, ob die folgenden Aussagen wahr oder falsch sind. Begründe deine Überlegung z.B. mit einer Zeichnung.
- Ein rechtwinkliges Dreieck kann gleichschenklig sein.
- Jedes gleichseitige Dreieck ist immer spitzwinklig.
- Ein stumpfwinkliges Dreieck kann rechtwinklig sein.
1. Ja, es kann gleichschenklig sein. Es ist ein Dreieck mit zweimal 45° Winkeln und einem rechten Winkel.
2. Ja, das stimmt. In einem gleichseitiges Dreieck sind alle Winkel 60°.
3. Das ist nicht wahr. Versuche mal ein Dreieck zu zeichnen, das einen stumpfen Winkel und einen rechten Winkel hat. Dann fällt dir vielleicht auf, dass das nicht möglich ist.