Benutzer:L.hodankov/Wurzeln: Unterschied zwischen den Versionen
(Lernpfad kopiert) Markierung: Quelltext-Bearbeitung 2017 |
(Aufgaben ausgetauscht) Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 44: | Zeile 44: | ||
* Nr. 13 - 17|Üben}}<br><br> | * Nr. 13 - 17|Üben}}<br><br> | ||
Jetzt bist du fit für Aufgaben aus dem Buch: | Jetzt bist du fit für Aufgaben aus dem Buch: | ||
{{Box|Übung 2(*)|Löse die Aufgaben | {{Box|Übung 2(*)|Löse die Aufgaben bei Learningapps. | ||
|Üben}} | |||
{{LearningApp|app=pztkgmhsk21|width=100%|height=400px}} | |||
<br> | <br> | ||
{{Box|Übung 3(**)|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und ergänze die Lösungen, ohne den Taschenrechner zu benutzen. | {{Box|Übung 3(**)|Löse die Aufgaben aus dem Buch. Schreibe die Aufgabe ab und ergänze die Lösungen, ohne den Taschenrechner zu benutzen. | ||
Version vom 29. November 2021, 14:04 Uhr
1) Potenzen: Definition
2) Potenzgesetze
3) Sehr große und sehr kleine Zahlen: Wissenschaftliche Schreibweise
4) Wurzeln: Definition
SEITE IM AUFBAU!!
4 Wurzeln/Quadratwurzeln - Definition
4.1 Wurzeln - Einführung

4.2 (Quadrat)wurzel - Definition
Teste dich:
Wiederholung Quadratzahlen:
11² = 121
12² = 144
13² = 169
14² = 196
15² = 225
16² = 256
17² = 289
18² = 324
19² = 361
20² = 400
Jetzt bist du fit für Aufgaben aus dem Buch:
Berechne zunächst die Fläche des Rechtecks A = a∙b
a) A = 18∙8 = 144
Nun überlege, welche Seitenlänge das Quadrat mit dem Flächeninhalt A = 144 (m²) besitzt:
144 = a² |
= a
12 = a
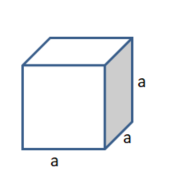
Die Oberfläche eines Würfels besteht aus 6 Quadraten:
O = 6a²
24 = 6a² |:6
4 = a² |
Wenn 100 Quader in eine Reihe gelegt werden, entstehen 4∙100 + 2 = 402 quadratische Flächen mit dem Flächeninhalt a². Es gilt also O = 402a².
Zähle die Quadratflächen, die zur Oberfläche gehören.
Lösung zu a) 22 Quadrate
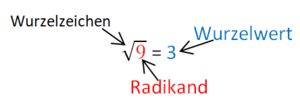
4.3 Irrationale Zahlen - Bestimmen von Quadratwurzeln
Quadratwurzeln von Zahlen, die keine Quadratzahl sind, lassen sich nur annähern.
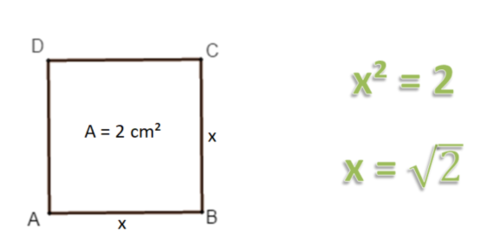
So liegt z.B. der Wert von im Intervall [1;2], also zwischen und 1 und 2, denn 1² < 2 < 2².
Dieses Intervall kannst du verkleinern, um den Wert von auf mehrere Nachkommastellen anzunähern. Das nachfolgende Applet verdeutlicht dieses Vorgehen, die sogenannte Intervallschachtelung:

(Applet von W. Wengler)
hat unendlich viele Nachkommaziffern, die nie periodisch werden. Man kann diese Zahl also nicht als Bruch darstellen.
Den meisten ist es zwar egal, doch ist irrational...
4.4 Konstruktion von
Ziehe den Schieberegler:

4.4 Kubikwurzeln - 3. Wurzel
Wenn du die Kantenlänge eines Würfels mit einem Volumen von 8cm³ bestimmen möchtest, muss du die Zahl finden, die dreimal mit sich selbst multipliziert 8 ergibt:
222 = 23 = 8, die Kubikwurzel ist dann wie folgt definiert:
=2
Die 3. Wurzel aus 8 ist 2. Die 3. Wurzel heißt auch Kubikwurzel (von engl. "cube" = Würfel).
Beachte Schreibweisen:
geg: V = 512 cm³; ges: Kantenlänge a
a3 = 512 |
a =
Beachte, dass du zwei Würfel gegeben hast, also gilt:
2a3 = 843,75 |:2