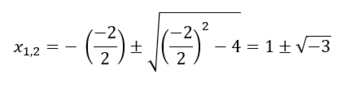Benutzer:Stoll-Gym10Erfurt/Formeln: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Keine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 5: Zeile 5:
<nowiki>{{Box|1 = </nowiki><span style="color: green">  Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br />  
<nowiki>{{Box|1 = </nowiki><span style="color: green">  Aufgabe 7.3 </span>| 2 = Löse folgende quadratische Gleichungen. <br /> <br />  


<span style="color: green" style="font-size:24pt"> a)  Fehler beim Darstellen von Formeln  </span> <br/> <br />  
<span style="font-size:24pt"> a)  Fehler beim Darstellen von Formeln  </span> <br /> <br />  
<span style="color: green"> b) </span> Fehler beim Darstellen von Formeln <br/> <br/>
<span style="color: green"> b) </span> Fehler beim Darstellen von Formeln <br /> <br />


{{Lösung versteckt
{{Lösung versteckt
Zeile 40: Zeile 40:
|3=Arbeitsmethode}}
|3=Arbeitsmethode}}


<span style="color: Blue" style="font-size:24pt"> Mit Bild einfügen kann man die Sache korrigieren  </span>  
<span style="font-size:20pt"> Mit Bild einfügen kann man Parser-Fehler korrigieren/umgehen </span>  


[[Datei:TG Lösung zu A7.3a.png|350px|Lösung zu Aufgabe 7.3a im Kapitel Terme und Gleichungen des Lernpfads "Wie Funktionen funktionieren 2.0"(nicht korrekt via Mathe-Umgebung darstellbar)]]
[[Datei:TG Lösung zu A7.3a.png|350px|Lösung zu Aufgabe 7.3a im Kapitel Terme und Gleichungen des Lernpfads "Wie Funktionen funktionieren 2.0"(nicht korrekt via Mathe-Umgebung darstellbar)]]

Version vom 11. Oktober 2021, 15:53 Uhr

Quelltext aus Terme und Gleichungen:

{{Box|1 =  Aufgabe 7.3 | 2 = Löse folgende quadratische Gleichungen.

a) Fehler beim Darstellen von Formeln

b) Fehler beim Darstellen von Formeln

Eine quadratische Gleichung kann 2, 1 oder 0 Lösungen haben. Sortiere dir die Summanden der Gleichung. Bringe die Gleichung zum Beispiel in die Form, in der du die pq- Formel anwenden kannst.

a) Diese Aufgabe hat keine Lösung (in den reellen Zahlen). Berechnet man die Lösung der Gleichung mit der pq- Formel
Hier steht eigentlich die Formel

, so sieht man, dass der Radiant negativ ist und somit die Gleichung nicht in den reellen Zahlen gelöst werden kann.  
b)  x_1 = 3 ; x_2 = -1


Aufgabe 2

Füge die zugehörigen Terme zusammen. Du kannst hierfür deinen Stift und Papier nutzen.


Überlege über welchen Weg du den Term am besten vereinfachen kannst. Schaue dir dafür in der Wiederholung "Terme - Vereinfachen" die verschiedneen Wege nochmal an.

Markiere dir die im Term zusammengehörenden Teilterme und sortiere sie der Reihe nach. z.B: 2x + 3 - 3x -

2

Mit Bild einfügen kann man Parser-Fehler korrigieren/umgehen

Lösung zu Aufgabe 7.3a im Kapitel Terme und Gleichungen des Lernpfads "Wie Funktionen funktionieren 2.0"(nicht korrekt via Mathe-Umgebung darstellbar)

Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Stoll-Gym10Erfurt/Formeln&oldid=53417“