Herta-Lebenstein-Realschule/Lernpfad Kreis und Winkel/1) Kreis

1. Kreis

1.1 Kreise erkennen

Idee

Schaue dich in deiner Umgebung um. Welche kreisförmigen Gegenstände findest du? Notiere.

Übung x: Kreise erkennen

Bearbeite die folgende LearningApp.

Übung x: Aufgaben im Buch

Bearbeite die folgende Aufgabe im Heft.

• S. 11, Nr. 4a

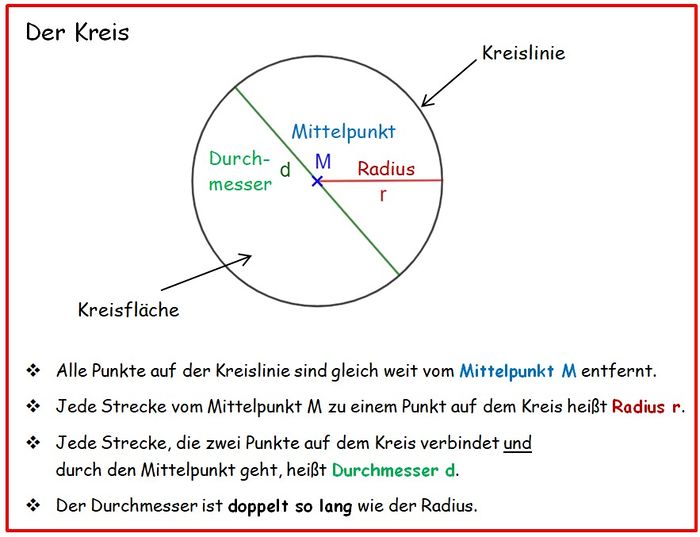
1.2 Fachbegriffe im Kreis

Merke: Der Kreis

Übung x: Fachbegriffe im Kreis

Bearbeite die folgenden LearningApps.

Übung x: Radius und Durchmesser bestimmen und berechnen

Bearbeite die folgende Online-Übung.

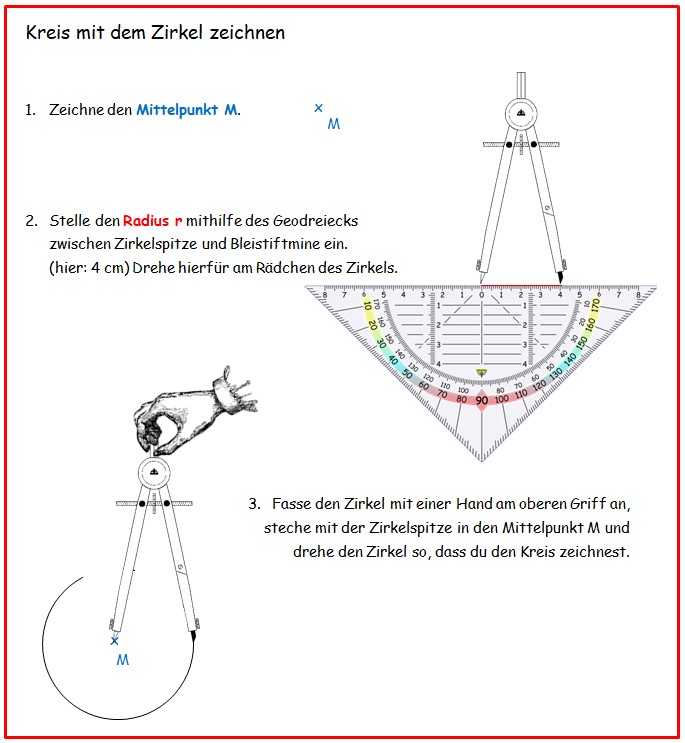
1.3 Kreise zeichnen

Erklärvideo x

Schau dir das Video zu Kreis mithilfe des Zirkels zeichnen an.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Info

Merke:

Übung x: Kreis mit dem Zirkel zeichnen

Bearbeite die folgende LearningApp.

Übung x: Aufgaben im Buch

Bearbeite die folgenden Aufgaben im Heft.

• S. 11, Nr. 2
• S. 11, Nr. 3
• S. 11, Nr. 5
• S. 11, Nr. 6

Aufgabe Nr. 6 rauslassen oder als Zusatz zum Knobeln nehmen?!
Sobald man die Lösung (oder einen Tipp) angibt, müssen die Schüler nichts mehr machen... und schreiben wieder nur ab. Und ohne Tipp oder Lösung werden sie es wahrscheinlich nicht hinbekommen.

ACHTUNG: Achte darauf, ob der Radius oder der Durchmesser angegeben ist!

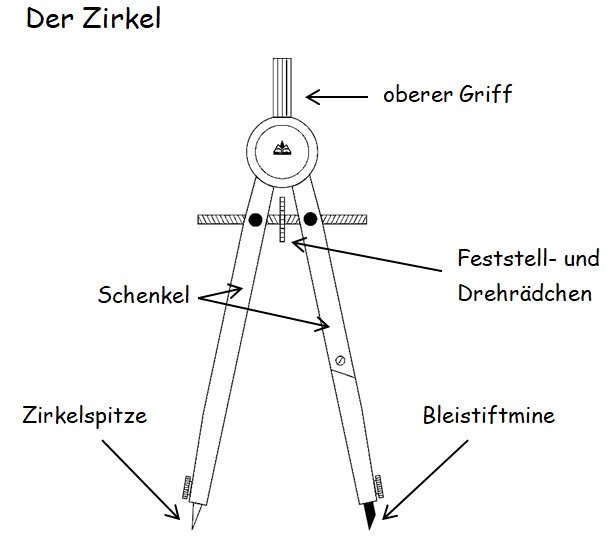
• Stelle den Radius mithilfe des Geodreiecks ein, indem du den entsprechenden Abstand zwischen Zirkelspitze und Bleistiftmine einstellst.
  
• Wandle dm zunächst in cm oder mm um. Denke an die Umrechnungszahl bei Längeneinheiten.

erforderlich?!
nö ;)

• zu a und b) Zeichne zunächst den Mittelpunkt ein und stelle dann den gewünschten Radius bzw. Durchmesser ein.
  
• zu c) Zeichne die Punkte M und P ein. Denke daran, dass M der Mittelpunkt ist. Die Verbindung zwischen M und P ist die Länge des Radius.
  

Folgenden Hinweis ergänzen? Wähle für die Aufgabenteile a) und b) als Einheit 1 cm und

wähle für den Aufgabenteil c) als Einheit 1 Kästchen.

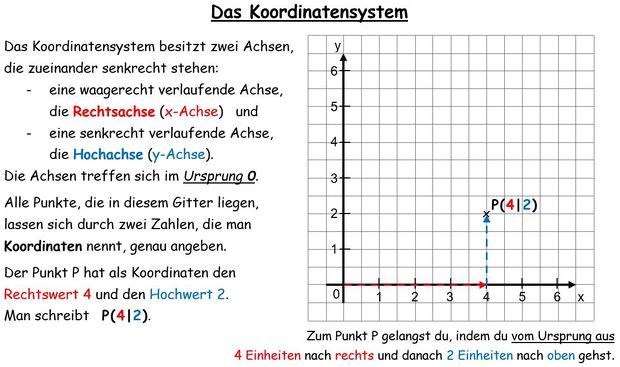
KONTROLLE: Überprüfe jeweils, ob der angegebene Punkt auf der Kreislinie des von dir gezeichneten Kreises liegt.
Wenn JA, hast du alles richtig gemacht.
Wenn NEIN, musst du die Aufgabe berichtigen (= noch einmal neu bearbeiten).
a) P(6/8)
b) P(7/12)

a) Q(2/10)

a) Zwei Kreise berühren sich nicht, wenn die Entfernung ihrer Mittelpunkte größer ist als die Summe ihrer Radien.
b) Zwei Kreise schneiden sich, wenn die Entfernung ihrer Mittelpunkte kleiner ist als die Summe ihrer Radien.

c) Zwei Kreise berühren sich, wenn die Entfernung ihrer Mittelpunkte der Summe ihrer Radien entspricht.

muss nicht, oder?!

noch ergänzen

noch ergänzen

1.4 Muster mit Zirkel zeichnen und ergänzen

Übung x: Aufgaben im Buch

Bearbeite die folgenden Aufgaben im Heft.

• S. 11, Nr. 8
• S. 11, Nr. 9
• S. 11, Nr. 10 [Zusatzaufgabe]

noch ergänzen

noch ergänzen

noch ergänzen

noch ergänzen

noch ergänzen

noch ergänzen

zurück zum Vorwissen

2) Winkel