Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Proportionale Zuordnungen: Unterschied zwischen den Versionen
K (Bildgröße) Markierung: Quelltext-Bearbeitung 2017 |
KKeine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{{Navigation|[[Buss-Haskert/Lernpfad Zuordnungen und Dreisatz| 1. Zuordnungen]]<br>[[Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Proportionale Zuordnungen| 2. Proportionale Zuordnungen und Dreisatz]]<br>[[Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Umgekehrt proportionale Zuordnungen| 3. Umgekehrt proportionale Zuordnungen und Dreisatz]]<br>[[Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Bunte Mischung|4. Bunte Mischung - Übungen]]}} | {{Fortsetzung|vorher=zurück zur Seite der Herta-Lebenstein-Realschule|vorherlink=Herta-Lebenstein-Realschule}} | ||
{{Navigation|[[Benutzer:Buss-Haskert/Lernpfad Zuordnungen und Dreisatz| 1. Zuordnungen]]<br>[[Benutzer:Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Proportionale Zuordnungen| 2. Proportionale Zuordnungen und Dreisatz]]<br>[[Benutzer:Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Umgekehrt proportionale Zuordnungen| 3. Umgekehrt proportionale Zuordnungen und Dreisatz]]<br>[[Benuzter:Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Bunte Mischung|4. Bunte Mischung - Übungen]]<br>[[Benutzer:Buss-Haskert/Lernpfad Zuordnungen und Dreisatz/Checkliste|5. Checkliste]]}} | |||
===2. Proportionale Zuordnungen und Dreisatz=== | ===2. Proportionale Zuordnungen und Dreisatz=== | ||
| Zeile 25: | Zeile 27: | ||
{{#ev:youtube|MT3hVo_BfT0|600|center}} | {{#ev:youtube|MT3hVo_BfT0|600|center}} | ||
{{Box|Übung 6: Proportionale Zuordnungen erkennen|Bearbeite die folgenden Learningapps. Welche Strategien nutzt du, um zu entscheiden, ob die Zuordnungen proportional sind oder nicht? Diskutiere deine Ideen mit deinem Partner.|Üben}} | {{Box|Übung 6: Proportionale Zuordnungen erkennen|Bearbeite das Quiz und die folgenden Learningapps. Welche Strategien nutzt du, um zu entscheiden, ob die Zuordnungen proportional sind oder nicht? Diskutiere deine Ideen mit deinem Partner.|Üben}} | ||
<div class="schuettel-quiz"> | |||
Die Zuordnung Gewicht des Käses (g) → Preis (€) ist proportional, denn '''doppelt''' so viel Käse kostet '''doppelt''' so viel.<br>Die Zuordnung Alter eines Kindes → Körpergröße ist nicht proportional, denn wenn ein Kind '''doppelt''' so alt ist, ist es nicht auch '''doppelt''' so groß. | |||
</div> | |||
{{LearningApp|app=prosu2nhj19|width=100%|height=500px}} | {{LearningApp|app=prosu2nhj19|width=100%|height=500px}} | ||
{{LearningApp|app=pmqo5urxn19|width=100%|height=500px}} | {{LearningApp|app=pmqo5urxn19|width=100%|height=500px}} | ||
| Zeile 57: | Zeile 62: | ||
{{LearningApp|app=pgegxqvbc20|width=100%|height=1500px}} | {{LearningApp|app=pgegxqvbc20|width=100%|height=1500px}} | ||
{{Box|Übung 9: Dreisatz bei proportionalen Zuordnungen|Löse Buch S. 36 Nr. 1, 3, 4, 7 und 8 in deinem Heft. Gib die Zuordnung an und prüfe, ob diese proportional ist. Rechne dann mit dem Dreisatz (Tabelle).|Üben}} | {{Box|Übung 9: Dreisatz bei proportionalen Zuordnungen|Löse Buch S. 36 Nr. 1, 3, 4, 6, 7 und 8 in deinem Heft. Gib die Zuordnung an und prüfe, ob diese proportional ist. Rechne dann mit dem Dreisatz (Tabelle).|Üben}} | ||
{{Lösung versteckt|Du musst nicht immer die Einheit (1) als Zwischengröße wählen. Der Wert, den du als Zwischenschritt wählst, muss nur ein Teiler der beiden Eingabegrößen sein. Hier bietet sich als Zwischenwert 250g an:[[Datei:Tipp zu Nr. 7 S. 36.png|ohne|mini]]<br> In Teil b) bietet sich 0,5 kg als Zwischengröße an und in Teil c) 0,90€.|Tipp zu Nr. 7|Verbergen}} | {{Lösung versteckt|Du musst nicht immer die Einheit (1) als Zwischengröße wählen. Der Wert, den du als Zwischenschritt wählst, muss nur ein Teiler der beiden Eingabegrößen sein. Hier bietet sich als Zwischenwert 250g an:[[Datei:Tipp zu Nr. 7 S. 36.png|ohne|mini]]<br> In Teil b) bietet sich 0,5 kg als Zwischengröße an und in Teil c) 0,90€.|Tipp zu Nr. 7|Verbergen}} | ||
{{Lösung versteckt|1=Bestimme zunächst die Fläche der Wand, die schon gestrichen wurde.<br>Flächeninhalt (Rechteck) = Länge·Breite|2=Tipp zu Nr. 8|3=Verbergen}} | {{Lösung versteckt|1=Bestimme zunächst die Fläche der Wand, die schon gestrichen wurde.<br>Flächeninhalt (Rechteck) = Länge·Breite|2=Tipp zu Nr. 8|3=Verbergen}} | ||
Aktuelle Version vom 22. März 2021, 17:20 Uhr
2. Proportionale Zuordnungen und Dreisatz
3. Umgekehrt proportionale Zuordnungen und Dreisatz
4. Bunte Mischung - Übungen
5. Checkliste
2. Proportionale Zuordnungen und Dreisatz
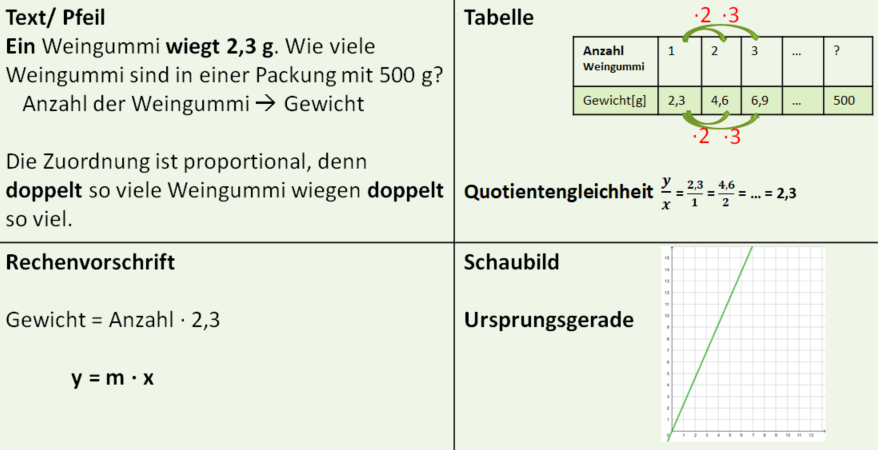
Mögliche Darstellungen sind die Textform, eine Wertetabelle, der Graph (Schaubild) und die Rechenvorschrift.
2.1 Proportionale Zuordnungen erkennen
Zusammenfassung:
Die Zuordnung Gewicht des Käses (g) → Preis (€) ist proportional, denn doppelt so viel Käse kostet doppelt so viel.
Die Zuordnung Alter eines Kindes → Körpergröße ist nicht proportional, denn wenn ein Kind doppelt so alt ist, ist es nicht auch doppelt so groß.
Das nachfolgende Video erklärt, wie du die Proportionalität bei Wertetabellen prüfen kannst (Quotientengleichheit)
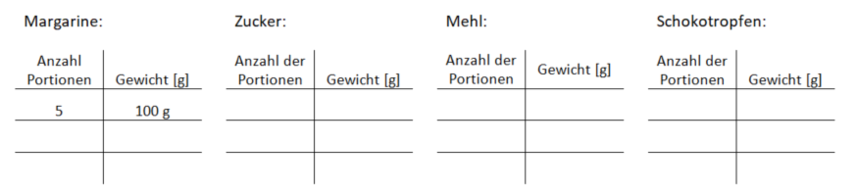
2.2 Dreisatz bei proportionalen Zuordnungen: Mathematik richtig lecker!
Die Zuordnung lautet: Anzahl der Portionen Menge der Zutat.
Die Zuordnung Anzahl der Portionen Menge der Zutat ist proportional, denn für doppelt so viele Portionen benötigt man auch die doppelte Menge der Zutaten. Daher können wir mit drei Schritten die Mengen für ein Klassenrezept berechnen:

In Teil b) bietet sich 0,5 kg als Zwischengröße an und in Teil c) 0,90€.
Flächeninhalt (Rechteck) = Länge·Breite
2.3 Angebote vergleichen
Ein Supermarkt bietet eine 150g-Packung Cookies für 1,95 an.
Auf dem Markt werden selbst gebackene Cookies in Tüten zu je 250g für 3,00€ verkauft.
Vergleiche die Angebote.
Supermarkt:
150g 1,95
50g 0,65€
Markt:
250g 3,00
50g 0,60€
2.4 Vermischte Übungen zu proportionalen Zuordnungen