Benutzer:Schulten/Dreiecke/Winkelsumme im Dreieck: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
K (→3. Übe selbstständig!: Anweisungen zur Bearbeitung ergänzt.) Markierung: 2017-Quelltext-Bearbeitung |
Markierung: 2017-Quelltext-Bearbeitung |
||
| (25 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
<br /> | |||
{{Fortsetzung|vorher=zurück zum Vorwissen |vorherlink= | {{Fortsetzung|vorher=zurück zum Vorwissen |vorherlink=Benutzer:Schulten/Dreiecke}}<br> | ||
=====1. Probiere aus!===== | =====1. Probiere aus!===== | ||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">{{Box|Aufgabe|Nimm dir einen Zettel.<br> | <div class="width-1-2">{{Box|Aufgabe 1|Nimm dir einen Zettel.<br> | ||
Zeichne mit deinem Geodreick ein Dreieck.<br> | Zeichne mit deinem Geodreick ein Dreieck.<br> | ||
Schneide das Dreieck aus.<br> | Schneide das Dreieck aus.<br> | ||
| Zeile 13: | Zeile 13: | ||
<br /></div> | <br /></div> | ||
</div> | </div> | ||
=====2. Merke dir!===== | =====2. Merke dir!===== | ||
Notiere diesen Kasten in deiner Kladde. | |||
<div class="grid"> | <div class="grid"> | ||
<div class="width-1-2">{{Box|1=Merke|2=Die Winkelsumme in einem Dreieck beträgt immer 180°. <br> | <div class="width-1-2">{{Box|1=Merke|2=Die Winkelsumme in einem Dreieck beträgt immer 180°. <br> | ||
| Zeile 20: | Zeile 22: | ||
Für ein Dreieck wissen wir, dass α = 32° und β = 110° groß sind.<br> | Für ein Dreieck wissen wir, dass α = 32° und β = 110° groß sind.<br> | ||
Nun können wir den fehlenden Winkel γ berechnen:<br> | Nun können wir den fehlenden Winkel γ berechnen:<br> | ||
32° + 110° + γ = 180°<br> | '''32° + 110° + γ = 180°'''<br> | ||
142° + γ = 180°<br> | '''142° + γ = 180°<br>''' | ||
γ = 38°|3=Kurzinfo}} | '''γ = 180° - 142°<br>''' | ||
'''γ = 38°'''|3=Kurzinfo}} | |||
<br /></div> | <br /></div> | ||
</div> | </div> | ||
=====3. Übe selbstständig!===== | =====3. Übe selbstständig!===== | ||
Wie du es aus unserem Unterricht schon kennst, sollst du auch '''jetzt '''mithilfe deines Buches und deines Arbeitsheftes '''üben'''. | Wie du es aus unserem Unterricht schon kennst, sollst du auch '''jetzt '''mithilfe deines Buches und deines Arbeitsheftes '''üben'''. <br> | ||
Die | |||
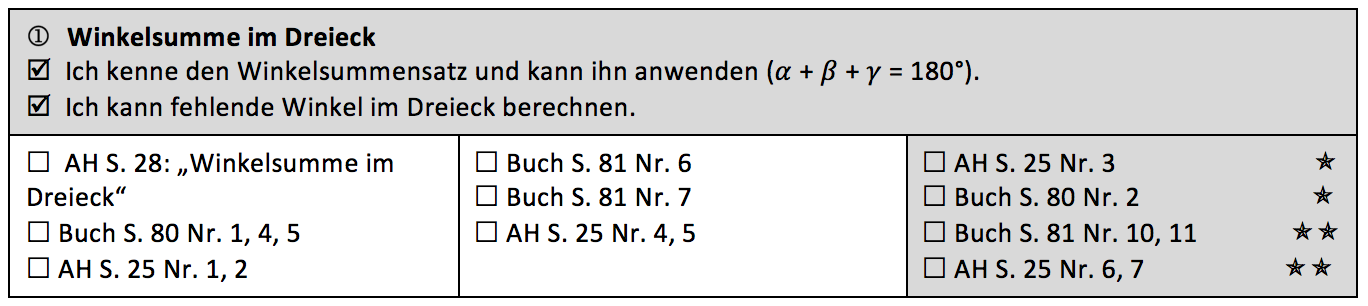
Von der Aufgaben aus der '''zweiten und dritten Spalte''' sollst du dir insgesamt mindestens ''' | {{Box|Aufgabe 2|Die '''Grundaufgaben''' (erste Spalte) musst du '''komplett bearbeiten'''. <br> | ||
Arbeite gründlich und achte darauf, dass du alle Lösungswege vollständig und ordentlich notierst. Hast du in deinem Arbeitsheft nicht genug Platz, arbeite bitte in deinem Heft.<br> | Von der Aufgaben aus der '''zweiten und dritten Spalte''' sollst du dir insgesamt mindestens '''fünf Aufgaben''' aussuchen.<br> | ||
Arbeite gründlich und achte darauf, dass du alle Lösungswege vollständig und ordentlich notierst. Hast du in deinem Arbeitsheft nicht genug Platz, arbeite bitte in deinem Heft.|Arbeitsmethode}}<br> | |||
[[Datei:Bildschirmfoto 2021-02-01 um 11.50.46.png|800|center]] | [[Datei:Bildschirmfoto 2021-02-01 um 11.50.46.png|800|center]] | ||
<br> | |||
=====4. Nutze Tipps!===== | =====4. Nutze Tipps!===== | ||
{{Box|Info|Du benötigst noch einmal eine Erklärung, kannst aber gerade niemanden fragen? Dann nutze dieses Video als Hilfe.|Kurzinfo}} | |||
{{#ev:youtube|YwUIBBE7Fvk|800|center}} | |||
<br> | |||
=====5. Übe online!===== | =====5. Übe online!===== | ||
=====6. Kontrolliere | {{Box|Aufgabe 3|Wähle eine der LearningApps aus und übe noch einmal zur Winkelsumme im Dreieck.|Üben}}<br> | ||
{{LearningApp|app=prnoxy7b221|width=100%|height=400px}} | |||
<br> | |||
<br> | |||
{{LearningApp|app=pn5vwk3uk21|width=100%|height=400px}} | |||
<br> | |||
<br> | |||
{{LearningApp|app=psc8ny58t21|width=100%|height=400px}} | |||
<br> | |||
<br> | |||
=====6. Kontrolliere!===== | |||
{{Box|Lösungen|In deinem Mathekanal in Teams findest du die Lösungen zu deinen Seiten aus dem Buch.<br> | |||
Kontrolliere deine Lösungen. <br> | |||
Markiere Fehler und notiere das richtige Ergebnis.<br> | |||
Überlege, was du falsch gemacht hast. <br> | |||
Wenn du den Fehler nicht findest, frage deine Lehrkraft um Hilfe.|Lösung}} | |||
<br> | |||
''' | =====7. Test dich!===== | ||
{{h5p-zum|id=11109 |heigth=600px}} | |||
<br> | |||
<br> | |||
'''{{Fortsetzung|weiter=weiter zu Schritt 2 - Dreiecksformen |weiterlink=Benutzer:Schulten/Dreiecke/Dreiecksformen}}''' | |||
Aktuelle Version vom 4. März 2021, 09:41 Uhr
1. Probiere aus!
2. Merke dir!
Notiere diesen Kasten in deiner Kladde.
3. Übe selbstständig!
Wie du es aus unserem Unterricht schon kennst, sollst du auch jetzt mithilfe deines Buches und deines Arbeitsheftes üben.
4. Nutze Tipps!
5. Übe online!
6. Kontrolliere!
7. Test dich!