Benutzer:Buss-Haskert/Pythagoras/Satz des Pythagoras: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
K (Übungen ergänzt)
Markierung: 2017-Quelltext-Bearbeitung
K (video ergänzt)
Markierung: 2017-Quelltext-Bearbeitung
Zeile 1: Zeile 1:
SEITE IM AUFBAU!
SEITE IM AUFBAU!
== 2 Satz des Pythagoras ==


=== 2.1 12-Knoten-Seil ===
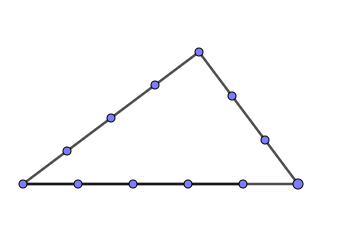
{{Box|12-Knoten-Seil|Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten. <br>
{{Box|12-Knoten-Seil|Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten. <br>
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast.
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast.
Zeile 15: Zeile 17:


<br>
<br>
=== 2.2 Satz des Pythagoras ===
<ggb_applet id="AgezqDax" width="900" height="550" border="888888" />
<ggb_applet id="AgezqDax" width="900" height="550" border="888888" />
<small>Applet von Pöchtrager</small>
<small>Applet von Pöchtrager</small>
Zeile 41: Zeile 44:
<ggb_applet id="ND4QUNXn" width="900" height="550" border="888888" />
<ggb_applet id="ND4QUNXn" width="900" height="550" border="888888" />
<small>Applet von Pöchtrager</small>
<small>Applet von Pöchtrager</small>
<br>
Beweis Nr. 4:<br>
{{#ev:youtube|CAkMUdeB06o|800|center}}
<br>
Auch im Lied von Dorfuchs findest du einen Beweis für den Satz des Pythagoras:
{{#ev:youtube|8IZ_0qhZ36M|800|center}}
<br>
<br>
<br>


Zeile 56: Zeile 66:
* S. 111 Nr. 3|Üben}}
* S. 111 Nr. 3|Üben}}
{{Lösung versteckt|1=In Nr. 3 gibt es jeweils 3 rechtwinklige Dreiecke pro Figur, das große gesamte Dreieck mit den Katheten x und y und der Hypotenuse (z+w) und die zwei kleinen Dreiecke mit jeweils der Seite y als Kathete.|2=Tipp zu Nr. 3|3=Verbergen}}
{{Lösung versteckt|1=In Nr. 3 gibt es jeweils 3 rechtwinklige Dreiecke pro Figur, das große gesamte Dreieck mit den Katheten x und y und der Hypotenuse (z+w) und die zwei kleinen Dreiecke mit jeweils der Seite y als Kathete.|2=Tipp zu Nr. 3|3=Verbergen}}
=== 2.3 Fehlende Seitenlängen in rechtwinkligen Dreiecken berechnen mit dem Satz des Pythagoras ===
Mithilfe des Satzes von Pythagoras lassen sich '''in rechtwinkligen''' Dreiecken fehlende Seitenlängen berechnen.<br>
Beispiel 1: Die Katheten sind gegeben und die Hypotenuse ist gesucht.<br>


{{Box|1=Fehlende Seitenlängen berechnen|2=Du kannst mithilfe des Satzes von Pythagoras fehlende Seitenlängen in rechtwinkligen Dreiecken berechnen....NOCH ERGÄNZEN|3=Arbeitsmethode}}
{{Box|1=Fehlende Seitenlängen berechnen|2=Du kannst mithilfe des Satzes von Pythagoras fehlende Seitenlängen in rechtwinkligen Dreiecken berechnen....NOCH ERGÄNZEN|3=Arbeitsmethode}}

Version vom 21. Januar 2021, 14:20 Uhr

SEITE IM AUFBAU!

2 Satz des Pythagoras

2.1 12-Knoten-Seil

12-Knoten-Seil

Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten.
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast.
Was beobachtest du?

12 Knoten Seil.png

Prüfe deine Beobachtung mithilfe des nachfolgenden Applets.

GeoGebra

Applet von Pöchtrager


Was hat das mit dem Satz des Pythagoras zu tun?


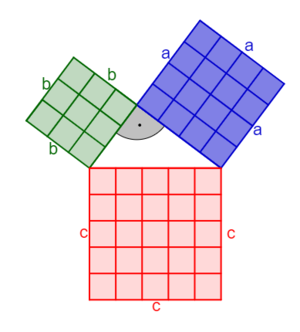
2.2 Satz des Pythagoras

GeoGebra

Applet von Pöchtrager

Satz des Pythagoras

In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse genauso groß wie die Summe der Quadrate über den Katheten.
Für ein rechtwinkliges Dreieck mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras

a² + b² = c².Pythagorasfigur 1.png


Überprüfe die Aussage des Satzes von Pythagoras mithilfe des nachfolgenden Applets.

GeoGebra

Applet von Pöchtrager


Zerlegungsbeweise
Es gibt viele Möglichkeiten, den Satz des Pythagoras zu beweisen. Die nachfolgenden GeoGebra-Applets nutzen die Zerlegungsmethode, d.h. die Quadrate über den Katheten werden so zerlegt, dass sie neu zusammengelegt das Hypotenusenquadrat ergeben. Erkläre jeweils!

Beweis Nr. 1:

GeoGebra

Applet von J. Mil
Beweis Nr. 2:

GeoGebra

Applet von B.Lachner
Beweis Nr. 3:

GeoGebra

Applet von Pöchtrager
Beweis Nr. 4:

Video laden
YouTube


Auch im Lied von Dorfuchs findest du einen Beweis für den Satz des Pythagoras:

Video laden
YouTube




Übung 1 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

  • 1
  • 2
  • 3
  • 4
  • 5
Danach bearbeite die Übungen der LearningApp.


Übung 2

Löse die Aufgaben aus dem Buch. Übertrage die Skizze in dein Heft, markiere die Hypotenuse rot und formuliere den Satz des Pythagoras. (Achte darauf, dass deine Skizze ein rechtwinkliges Dreieck ist.)

  • S. 111 Nr. 2
  • S. 111 Nr. 3
In Nr. 3 gibt es jeweils 3 rechtwinklige Dreiecke pro Figur, das große gesamte Dreieck mit den Katheten x und y und der Hypotenuse (z+w) und die zwei kleinen Dreiecke mit jeweils der Seite y als Kathete.

2.3 Fehlende Seitenlängen in rechtwinkligen Dreiecken berechnen mit dem Satz des Pythagoras

Mithilfe des Satzes von Pythagoras lassen sich in rechtwinkligen Dreiecken fehlende Seitenlängen berechnen.

Beispiel 1: Die Katheten sind gegeben und die Hypotenuse ist gesucht.



Fehlende Seitenlängen berechnen
Du kannst mithilfe des Satzes von Pythagoras fehlende Seitenlängen in rechtwinkligen Dreiecken berechnen....NOCH ERGÄNZEN


Übung 3 - online

Löse auf der Seite Aufgabenfuchs die Aufgaben

  • 6
  • 7
  • 8
  • 9
  • 10
  • 11
  • 12
  • 13
Danach bearbeite die Aufgaben in den GeoGebra-Applets.

Übungen (GeoGebra-Applets von Pöchtrager)

GeoGebra


GeoGebra


GeoGebra



Pythagorasbaum: (Appelt von Pöchtrager)

GeoGebra
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Pythagoras/Satz_des_Pythagoras&oldid=41910“