Benutzer:Buss-Haskert/Pythagoras/Satz des Pythagoras: Unterschied zwischen den Versionen

Aus ZUM Projektwiki
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
KKeine Bearbeitungszusammenfassung
Markierung: 2017-Quelltext-Bearbeitung
Zeile 20: Zeile 20:
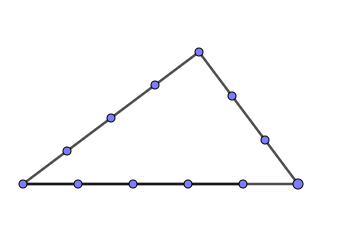
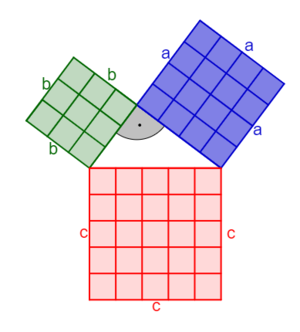
Für ein '''rechtwinkliges Dreiec'''k mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras<br>
Für ein '''rechtwinkliges Dreiec'''k mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras<br>
<big>'''<big>a² + b² = c²</big></big>'''.[[Datei:Pythagorasfigur 1.png|rahmenlos]]|3=Arbeitsmethode}}
<big>'''<big>a² + b² = c²</big></big>'''.[[Datei:Pythagorasfigur 1.png|rahmenlos]]|3=Arbeitsmethode}}
<br>
Überprüfe die Aussage des Satzes von Pythagoras mithilfe des nachfolgenden Applets.
<ggb_applet id="j3UksqZs" width="900" height="550" border="888888" />
<ggb_applet id="j3UksqZs" width="900" height="550" border="888888" />
<small>Applet von Pöchtrager</small>
<small>Applet von Pöchtrager</small>
<br>
<br>


{{Box|Zerlegungsbeweise|Es gibt viele Möglichkeiten, den Satz des Pythagoras zu beweisen. Die nachfolgenden GeoGebra-Applets nutzen die Zerlegungsmethode, d.h. die Quadrate über den Katheten werden so zerlegt, dass sie neu zusammengelegt das Hypotenusenquadrat ergeben. Erkläre jeweils!|Meinung}}


Zerlegungsbeweise:
Beweis Nr. 1:
<ggb_applet id="EdufUSRu" width="800" height="600" border="888888" />
<ggb_applet id="EdufUSRu" width="800" height="600" border="888888" />
<small>Applet von J. Mil</small>
<small>Applet von J. Mil</small>
<br>
<br>
Beweis Nr. 2:
<ggb_applet id="E5sNk6Z8" width="600" height="400" border="888888" />
<ggb_applet id="E5sNk6Z8" width="600" height="400" border="888888" />
<small>Applet von B.Lachner</small>
<small>Applet von B.Lachner</small>
<br>
<br>
Beweis Nr. 3:
<ggb_applet id="ND4QUNXn" width="900" height="550" border="888888" />
<ggb_applet id="ND4QUNXn" width="900" height="550" border="888888" />
<small>Applet von Pöchtrager</small>
<small>Applet von Pöchtrager</small>

Version vom 21. Januar 2021, 13:52 Uhr

SEITE IM AUFBAU!


12-Knoten-Seil

Schon im alten Ägypten (lange vor Pythagoras9), gab es Seilspanner, die mithilfe eines 12-Knoten-Seils Felder rechtwinklig einteilen konnten.
Probiere es aus: Teile ein Seil in 12 gleich lange Teile und mache jeweils einen Knoten bzw. markiere die Stelle des Seils farbig. Spanne nun das Seil so, dass du 5 Teile unten (Hypotenuse) und jeweils 3 bzw. 4 Teile an den Seiten (Katheten) hast.
Was beobachtest du?

12 Knoten Seil.png

Prüfe deine Beobachtung mithilfe des nachfolgenden Applets.

GeoGebra

Applet von Pöchtrager
Was hat das mit dem Satz des Pythagoras zu tun?


GeoGebra

Applet von Pöchtrager

Satz des Pythagoras

In jedem rechtwinkligen Dreieck ist das Quadrat über der Hypotenuse genauso groß wie die Summe der Quadrat über den Katheten.
Für ein rechtwinkliges Dreieck mit dem rechten Winkel γ (γ=90°) heißt der Satz des Pythagoras

a² + b² = c².Pythagorasfigur 1.png


Überprüfe die Aussage des Satzes von Pythagoras mithilfe des nachfolgenden Applets.

GeoGebra

Applet von Pöchtrager


Zerlegungsbeweise
Es gibt viele Möglichkeiten, den Satz des Pythagoras zu beweisen. Die nachfolgenden GeoGebra-Applets nutzen die Zerlegungsmethode, d.h. die Quadrate über den Katheten werden so zerlegt, dass sie neu zusammengelegt das Hypotenusenquadrat ergeben. Erkläre jeweils!

Beweis Nr. 1:

GeoGebra

Applet von J. Mil
Beweis Nr. 2:

GeoGebra

Applet von B.Lachner
Beweis Nr. 3:

GeoGebra

Applet von Pöchtrager


Übungen (GeoGebra-Applets von Pöchtrager)

GeoGebra


GeoGebra


GeoGebra



Pythagorasbaum: (Appelt von Pöchtrager)

GeoGebra
Abgerufen von „https://projekte.zum.de/index.php?title=Benutzer:Buss-Haskert/Pythagoras/Satz_des_Pythagoras&oldid=41904“