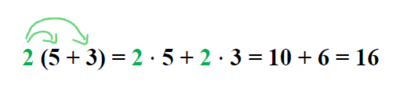Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (19 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 260: | Zeile 260: | ||
=====Aufgabe===== | =====Aufgabe===== | ||
{{Box | 1= Aufgabe 2: Wähle die richtige Antwort | 2= a) Was lässt sich sinnvollerweise ausklammern? | {{Box | 1= Aufgabe 2: Wähle die richtige Antwort | 2= '''a)''' Was lässt sich sinnvollerweise ausklammern? | ||
{{Lösung versteckt|1=Schaue dir (nochmal) die [[#Terme faktorisieren|Beispiele]] aus dem Video von Lehrer Schmidt an. | {{Lösung versteckt|1=Schaue dir (nochmal) die [[#Terme faktorisieren|Beispiele]] aus dem Video von Lehrer Schmidt an. | ||
|2=Tipp|3=Verbergen}} | |2=Tipp|3=Verbergen}} | ||
<br \> | <br \> | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
(i) <math> 9x - 15 </math> (!<math> 5 </math>) (<math> 3 </math>) (!<math> 9 </math>) (!<math> x</math>) <math> </math> | '''(i)''' <math> 9x - 15 </math> (!<math> 5 </math>) (<math> 3 </math>) (!<math> 9 </math>) (!<math> x</math>) <math> </math> | ||
(ii) <math> -36 + 12x </math> (!<math> 9 </math>) (<math> 12 </math>) (!<math> 24 </math>) (!<math> x</math>) | '''(ii)''' <math> -36 + 12x </math> (!<math> 9 </math>) (<math> 12 </math>) (!<math> 24 </math>) (!<math> x</math>) | ||
(iii) <math> 5xy + 4xz + 3x </math> (!<math> 5 </math>) (<math> x </math>) (!<math> y </math>) (!<math> 2z </math>) | '''(iii)''' <math> 5xy + 4xz + 3x </math> (!<math> 5 </math>) (<math> x </math>) (!<math> y </math>) (!<math> 2z </math>) | ||
</div> | </div> | ||
b) Wie sieht der erste Zwischenschritt beim Ausklammern aus? <br \> | '''b)''' Wie sieht der erste Zwischenschritt beim Ausklammern aus? <br \> | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe a) nach, was du ausklammerst. | {{Lösung versteckt|1=Schaue bei Teilaufgabe a) nach, was du ausklammerst. | ||
|2=Tipp|3=Verbergen}} | |2=Tipp|3=Verbergen}} | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
(i) <math> 9x - 15 </math> (<math> 3 \cdot 3x - 3 \cdot 5 </math>) (!<math> 3 \cdot 9x - 3 \cdot 5 </math>) (!<math> 3 \cdot 3x + 3 \cdot 5 </math>) (!<math> 3 \cdot x -15 </math>) | '''(i)''' <math> 9x - 15 </math> (<math> 3 \cdot 3x - 3 \cdot 5 </math>) (!<math> 3 \cdot 9x - 3 \cdot 5 </math>) (!<math> 3 \cdot 3x + 3 \cdot 5 </math>) (!<math> 3 \cdot x -15 </math>) | ||
(ii) <math> -36 + 12x </math> (<math> 12 \cdot [-3] + 12 \cdot x </math>) (!<math> 12 \cdot 3 + 12 \cdot x </math>) (!<math> 12 \cdot [-3] - 12 \cdot x </math>) (!<math> 12 \cdot [-3] + x </math>) | '''(ii)''' <math> -36 + 12x </math> (<math> 12 \cdot [-3] + 12 \cdot x </math>) (!<math> 12 \cdot 3 + 12 \cdot x </math>) (!<math> 12 \cdot [-3] - 12 \cdot x </math>) (!<math> 12 \cdot [-3] + x </math>) | ||
</div> | </div> | ||
c) Klammere komplett aus: | '''c)''' Klammere komplett aus: | ||
{{Lösung versteckt|1=Schaue bei Teilaufgabe a) nach, was du ausklammerst und bei b) wie dein erster Zwischenschritt aussieht. Mache zur Überprüfung die Probe wie es im Kapitel zum [[#Terme faktorisieren|''Faktorisieren'']] erklärt ist. <br /> | {{Lösung versteckt|1=Schaue bei Teilaufgabe a) nach, was du ausklammerst und bei b) wie dein erster Zwischenschritt aussieht. Mache zur Überprüfung die Probe wie es im Kapitel zum [[#Terme faktorisieren|''Faktorisieren'']] erklärt ist. <br /> | ||
|2=Tipp|3=Verbergen}} | |2=Tipp|3=Verbergen}} | ||
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
(i) <math> 9x - 15 </math> (<math> 3 \cdot [3x - 5] </math>) (!<math> 3 \cdot [9x - 15] </math>) (!<math> 3 \cdot [x - 5] </math>) (!<math> 3 \cdot [3x + 5] </math>) | '''(i)''' <math> 9x - 15 </math> (<math> 3 \cdot [3x - 5] </math>) (!<math> 3 \cdot [9x - 15] </math>) (!<math> 3 \cdot [x - 5] </math>) (!<math> 3 \cdot [3x + 5] </math>) | ||
(ii) <math> -36 + 12x </math> (<math> 12 \cdot [-3 + x] </math>) (!<math> 12 \cdot [3 + x ] </math>) (!<math> 12 \cdot [6 + 3x] </math>) (!<math> 3 \cdot [3 + x] </math>) | '''(ii)''' <math> -36 + 12x </math> (<math> 12 \cdot [-3 + x] </math>) (!<math> 12 \cdot [3 + x ] </math>) (!<math> 12 \cdot [6 + 3x] </math>) (!<math> 3 \cdot [3 + x] </math>) | ||
(iii) <math> 5xy + 4xz + 3x </math> (!<math> x \cdot [54yz + 3]</math>) (<math> x \cdot [5y + 4z + 3] </math>) (!<math> 2x \cdot [5y + 4z + 3]</math>) (!<math> 5 \cdot [xy + 4xz + 3x]</math>) | '''(iii)''' <math> 5xy + 4xz + 3x </math> (!<math> x \cdot [54yz + 3]</math>) (<math> x \cdot [5y + 4z + 3] </math>) (!<math> 2x \cdot [5y + 4z + 3]</math>) (!<math> 5 \cdot [xy + 4xz + 3x]</math>) | ||
</div> | </div> | ||
| 3= Arbeitsmethode | Farbe={{Farbe|orange}} }} | | 3= Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
| Zeile 320: | Zeile 320: | ||
| 3=Arbeitsmethode}} | | 3=Arbeitsmethode}} | ||
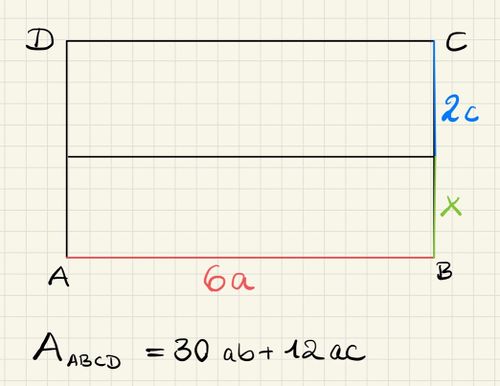
{{Box | 1= Aufgabe 4: Distributivgesetz veranschaulicht | 2= | {{Box | 1= Aufgabe 4: Distributivgesetz veranschaulicht | 2= '''a)''' Wie lang ist die Strecke <math> x </math>?<br /> | ||
[[Datei:Knobel .jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | [[Datei:Knobel .jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
{{Lösung versteckt|1=Was kannst du aus dem Term <math> 30ab+12ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | {{Lösung versteckt|1=Was kannst du aus dem Term <math> 30ab+12ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | ||
| Zeile 335: | Zeile 335: | ||
<math> x = </math> '''5b()''' | <math> x = </math> '''5b()''' | ||
</div> | </div> | ||
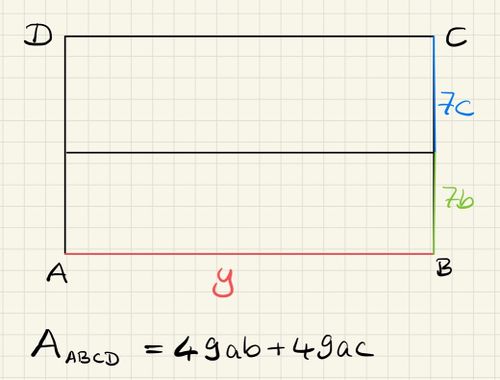
'''b)''' Wie lang ist die Strecke <math> y </math>?<br /> | |||
[[Datei:Knobelaufgabe.jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | [[Datei:Knobelaufgabe.jpg|500px|links]] <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
{{Lösung versteckt|1=Was kannst du aus dem Term <math> 49ab+49ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | {{Lösung versteckt|1=Was kannst du aus dem Term <math> 49ab+49ac </math>, der den Flächeninhalt des Rechtecks beschreibt, ausklammern? | ||
| Zeile 385: | Zeile 385: | ||
Für <math>a</math> und <math>b</math> können verschiedene Zahlen eingesetzt werden: <br \> | Für <math>a</math> und <math>b</math> können verschiedene Zahlen eingesetzt werden: <br \> | ||
a)<math>({\color{green}5}+{\color{blue}3})^2 = {\color{green}5}^2+2 \cdot {\color{green}5} \cdot {\color{blue}3}+{\color{blue}3}^2 = 25+30+9 = 64 (=8^2)</math> <br \> <br \> | a)<math>({\color{green}5}+{\color{blue}3})^2 = {\color{green}5}^2+2 \cdot {\color{green}5} \cdot {\color{blue}3}+{\color{blue}3}^2 = 25+30+9 = 64 (=8^2)</math> <br \> <br \> | ||
Für a und b können auch andere Variablen eingesetzt werden: <br \> | Für <math>a</math> und <math>b</math> können auch andere Variablen eingesetzt werden: <br \> | ||
b)<math>({\color{green}(uv)}+{\color{blue}w})^2 = {\color{green}(uv)}^2+2{\color{green}(uv)}{\color{blue}w}+{\color{blue}w}^2 = u^2v^2+2 \cdot uvw+w^2 </math> <br \> <br \> | b)<math>({\color{green}(uv)}+{\color{blue}w})^2 = {\color{green}(uv)}^2+2{\color{green}(uv)}{\color{blue}w}+{\color{blue}w}^2 = u^2v^2+2 \cdot uvw+w^2 </math> <br \> <br \> | ||
Selbst längere Terme kann man für a und b einsetzen: <br \> | Selbst längere Terme kann man für <math>a</math> und <math>b</math> einsetzen: <br \> | ||
c)<math>({\color{green}(2s+t)}+{\color{blue}u})^2 = {\color{green}(2s+t)}^2+2{\color{green}(2s+t)}{\color{blue}u}+{\color{blue}u}^2 </math> <br \> | c)<math>({\color{green}(2s+t)}+{\color{blue}u})^2 = {\color{green}(2s+t)}^2+2{\color{green}(2s+t)}{\color{blue}u}+{\color{blue}u}^2 </math> <br \> | ||
|2=Beispiele zur 1. binomischen Formel|3=Beispiele ausblenden}} | |2=Beispiele zur 1. binomischen Formel|3=Beispiele ausblenden}} | ||
| Zeile 410: | Zeile 410: | ||
<div class="zuordnungs-quiz"> | <div class="zuordnungs-quiz"> | ||
{{{!}} | {{{!}} | ||
{{!}} 1. binomische Formel {{!}}{{!}} <math forcemathmode="png">(x+19)^2</math> {{!}}{{!}} <math forcemathmode="png">({3\over 4}+p)^2</math> {{!}}{{!}} <math forcemathmode="png">(1,34+\sqrt{5})^2</math> | {{!}} 1. binomische Formel {{!}}{{!}} <math forcemathmode="png">(x+19)^2</math> {{!}}{{!}} <math forcemathmode="png">({3\over 4}+p)^2</math> {{!}}{{!}} <math forcemathmode="png">(1{,}34+\sqrt{5})^2</math> | ||
{{!}}- | {{!}}- | ||
{{!}} 2. binomische Formel {{!}}{{!}} <math forcemathmode="png">(19-x)^2</math> {{!}}{{!}} <math forcemathmode="png">(3-5)^2</math> {{!}}{{!}} <math forcemathmode="png">(25-y)^2</math> | {{!}} 2. binomische Formel {{!}}{{!}} <math forcemathmode="png">(19-x)^2</math> {{!}}{{!}} <math forcemathmode="png">(3-5)^2</math> {{!}}{{!}} <math forcemathmode="png">(25-y)^2</math> | ||
{{!}}- | {{!}}- | ||
{{!}} 3. binomische Formel {{!}}{{!}} <math forcemathmode="png">(5+t)(5-t)</math> {{!}}{{!}} <math forcemathmode="png">({3\over 8}-7)(7+{3\over 8})</math> {{!}}{{!}} | {{!}} 3. binomische Formel {{!}}{{!}} <math forcemathmode="png">(5+t)(5-t)</math> {{!}}{{!}} <math forcemathmode="png">({3\over 8}-7)(7+{3\over 8})</math> {{!}}{{!}} <math forcemathmode="png">(1{,}37-2)(1{,}37+2)</math> | ||
{{!}}- | {{!}}- | ||
{{!}} Das ist keine binomische Formel {{!}}{{!}} <math forcemathmode="png">(4+7)(5-7)</math> {{!}}{{!}} <math forcemathmode="png">(5+7)^{1\over 2}</math> {{!}}{{!}} <math forcemathmode="png">s+3^2</math> | {{!}} Das ist keine binomische Formel {{!}}{{!}} <math forcemathmode="png">(4+7)(5-7)</math> {{!}}{{!}} <math forcemathmode="png">(5+7)^{1\over 2}</math> {{!}}{{!}} <math forcemathmode="png">s+3^2</math> | ||
| Zeile 429: | Zeile 429: | ||
a) <math> 225+30a+a^2 = (</math>'''15()'''<math>+</math>'''a()'''<math>)^2 </math> <br /> | a) <math> 225+30a+a^2 = (</math>'''15()'''<math>+</math>'''a()'''<math>)^2 </math> <br /> | ||
b)<math> 9a^2-16b^2 = (</math>'''3a()'''<math>+</math>'''4b()'''<math>)\cdot ( </math>'''3a()'''<math>-</math>'''4b()''') <br /> | b) <math> 9a^2-16b^2 = (</math>'''3a()'''<math>+</math>'''4b()'''<math>)\cdot ( </math>'''3a()'''<math>-</math>'''4b()''') <br /> | ||
c)<math> 81u^2-36u+4 = (</math>'''9u()'''<math>-</math>'''2()'''<math>)^2 </math> <br /> | c) <math> 81u^2-36u+4 = (</math>'''9u()'''<math>-</math>'''2()'''<math>)^2 </math> <br /> | ||
d)<math> 4m^2+28m+49 = (</math>'''2m()'''<math>+</math>'''7()'''<math>)^2 </math> <br /> | d) <math> 4m^2+28m+49 = (</math>'''2m()'''<math>+</math>'''7()'''<math>)^2 </math> <br /> | ||
e)<math> 64y^2-160yz+100z^2 = (</math>'''8y()'''<math>-</math>'''10z()'''<math>)^2 </math> <br /> | e) <math> 64y^2-160yz+100z^2 = (</math>'''8y()'''<math>-</math>'''10z()'''<math>)^2 </math> <br /> | ||
f)<math> 36u^2-121w^2 = (</math>'''6u()'''<math>+</math>'''11w()'''<math>)\cdot ( </math>'''6u()'''<math>-</math>'''11w()''') <br /> | f) <math> 36u^2-121w^2 = (</math>'''6u()'''<math>+</math>'''11w()'''<math>)\cdot ( </math>'''6u()'''<math>-</math>'''11w()''') <br /> | ||
</div> | </div> | ||
Aktuelle Version vom 16. Dezember 2020, 12:05 Uhr
1) Terme zusammenfassen
Einführung
Aufgaben
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgaben zum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgaben