Digitale Werkzeuge in der Schule/Fit für VERA-8/Stochastik: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Markierung: Quelltext-Bearbeitung 2017 |
Markierung: Quelltext-Bearbeitung 2017 |
||
| (22 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 21: | Zeile 21: | ||
| 1= Was ist die absolute Häufigkeit? | | 1= Was ist die absolute Häufigkeit? | ||
| 2= | | 2= | ||
Die '''absolute Häufigkeit''' misst, wie oft ein bestimmtes Ereignis bei mehrmaliger Wiederholung eines Zufallsexperiments auftritt. Als Anzahl ist sie immer eine natürliche Zahl zwischen <math>0</math> und der Gesamtzahl von Versuchen. | Die '''absolute Häufigkeit''' misst, wie oft ein bestimmtes Ereignis bei mehrmaliger Wiederholung eines Zufallsexperiments auftritt. Als Anzahl ist sie immer eine natürliche Zahl zwischen <math>0</math> und der Gesamtzahl von Versuchen. | ||
| Zeile 33: | Zeile 31: | ||
| 2= | | 2= | ||
Wenn ein Würfel <math>100</math> mal geworfen wird und <math>22</math> mal die Würfelzahl | Wenn ein Würfel <math>100</math> mal geworfen wird und <math>22</math> mal die Würfelzahl 6 herauskommt, beträgt die absolute Häufigkeit dafür <math>22</math>. | ||
| 3= Hervorhebung1}} | | 3= Hervorhebung1}} | ||
| Zeile 50: | Zeile 48: | ||
| 2= | | 2= | ||
Bei <math>100</math> Würfen mit einem Würfel wird <math>22</math> mal die Würfelzahl | Bei <math>100</math> Würfen mit einem Würfel wird <math>22</math> mal die Würfelzahl 6 notiert. Die absolute Häufigkeit beträgt also <math>22</math> für die Würfelzahl 6. Um nun die relative Häufigkeit zu bestimmen, wird die absolute Häufigkeit durch die gesamte Anzahl an Würfelwürfen dividiert. | ||
In diesem Fall rechnet man: <math>\tfrac{22}{100} = 0{,}22</math> | In diesem Fall rechnet man: <math>\tfrac{22}{100} = 0{,}22</math> | ||
Die relative Häufigkeit, dass eine 6 gewürfelt wurde, hat einen Anteil von <math>\tfrac{22}{100}</math> von der gesamten Würfelrunde und dadurch einen Prozentanteil von <math>22{,}00</math> % <math>= 0{,}22 \cdot 100{,}00</math> %. | Die relative Häufigkeit, dass eine 6 gewürfelt wurde, hat einen Anteil von <math>\tfrac{22}{100}</math> von der gesamten Würfelrunde und dadurch einen Prozentanteil von <math>22{,}00</math> % <math>= 0{,}22 \cdot 100{,}00</math> %. | ||
| 3= Hervorhebung1}} | | 3= Hervorhebung1}} | ||
{{Box | {{Box | ||
| Zeile 64: | Zeile 60: | ||
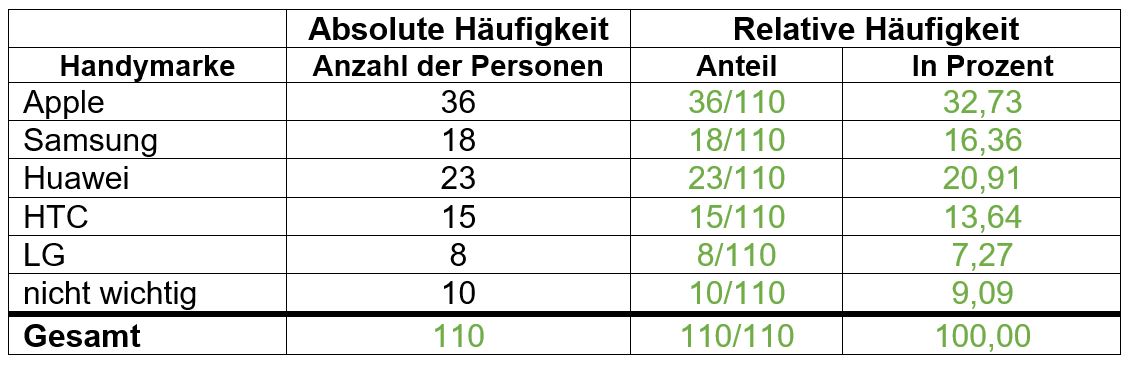
Auf dem Münsteraner Marktplatz wird eine Umfrage zum Thema Lieblingshandymarke durchgeführt. | Auf dem Münsteraner Marktplatz wird eine Umfrage zum Thema Lieblingshandymarke durchgeführt. | ||
<math>36</math> Personen beantworteten die Frage mit „Apple“, <math> | <math>10</math> Personen gaben bei der Umfrage an, dass ihnen die Handymarke nicht wichtig ist. <math>36</math> Personen beantworteten die Frage mit „Apple“, <math>8</math> Personen mit „LG“, <math>23</math> Personen mit „Huawei“, <math>15</math> Personen mit „HTC“ und <math>18</math> Personen mit „Samsung“. | ||
'''a)''' Fülle die Tabelle vollständig aus. Beachte, dass du den Bruch in folgender Form a/b eintippen solltest und ihn nicht kürzen darfst. | '''a)''' Fülle die Tabelle vollständig aus. Beachte, dass du den Bruch in folgender Form a/b eintippen solltest und ihn nicht kürzen darfst. | ||
| Zeile 76: | Zeile 72: | ||
! Anzahl der Personen | ! Anzahl der Personen | ||
! Anteil | ! Anteil | ||
! Prozent | ! in Prozent | ||
{{!-}} | {{!-}} | ||
{{!}} Apple | {{!}} Apple | ||
{{!}} <div class="lueckentext-quiz"> '''36()''' </div> | {{!}} <div class="lueckentext-quiz"> '''36()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''36/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''36/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''32,73 | {{!}} <div class="lueckentext-quiz"> '''32,73()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} Samsung | {{!}} Samsung | ||
{{!}} <div class="lueckentext-quiz"> '''18()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''18/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''16,36 | {{!}} <div class="lueckentext-quiz"> '''16,36()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} Huawei | {{!}} Huawei | ||
{{!}} <div class="lueckentext-quiz"> '''23()''' </div> | {{!}} <div class="lueckentext-quiz"> '''23()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''23/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''23/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''20,91 | {{!}} <div class="lueckentext-quiz"> '''20,91()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} HTC | {{!}} HTC | ||
{{!}} <div class="lueckentext-quiz"> '''15()''' </div> | {{!}} <div class="lueckentext-quiz"> '''15()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''15/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''15/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''13,64 | {{!}} <div class="lueckentext-quiz"> '''13,64()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} LG | {{!}} LG | ||
{{!}} <div class="lueckentext-quiz"> '''8()''' </div> | {{!}} <div class="lueckentext-quiz"> '''8()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''8/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''8/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''7,27 | {{!}} <div class="lueckentext-quiz"> '''7,27()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} nicht wichtig | {{!}} nicht wichtig | ||
{{!}} <div class="lueckentext-quiz"> '''10()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''10/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10/110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''9,09 | {{!}} <div class="lueckentext-quiz"> '''9,09()''' </div> | ||
{{!-}} | {{!-}} | ||
! Gesamt | ! Gesamt | ||
{{!}} <div class="lueckentext-quiz"> '''110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''110()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''110/110()''' </div> | {{!}} <div class="lueckentext-quiz"> '''110/110()''' </div> | ||
{{!}} <math>100{,}00</math> | {{!}} <math>100{,}00</math> | ||
{{!)}} | {{!)}} | ||
| Zeile 122: | Zeile 118: | ||
{{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | {{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | ||
{{Lösung versteckt| 1=[[Datei: | {{Lösung versteckt| 1= [[Datei:Lösung-1a.jpg|zentriert]] |2= Lösung |3= }} | ||
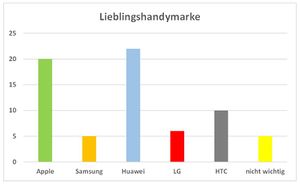
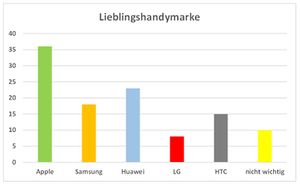
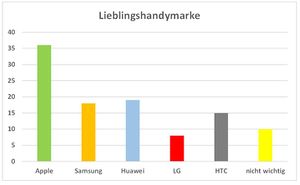
'''b)''' Die drei Bilder zeigen unterschiedliche Säulendiagramme. | '''b)''' Die drei Bilder zeigen unterschiedliche Säulendiagramme. | ||
| Zeile 151: | Zeile 147: | ||
{{Box | {{Box | ||
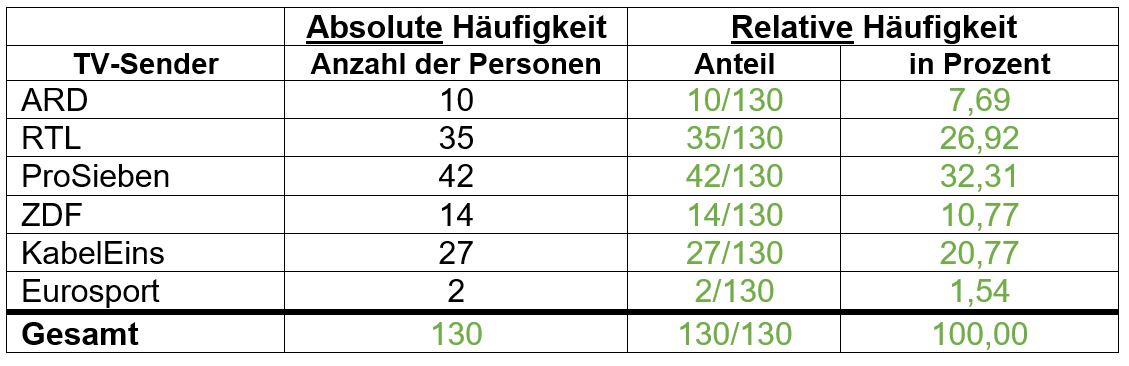
| 1= Aufgabe 2 | | 1= Aufgabe 2: TV Sender | ||
| 2= | | 2= | ||
| Zeile 214: | Zeile 168: | ||
! Anzahl der Personen | ! Anzahl der Personen | ||
! Anteil | ! Anteil | ||
! Prozent | ! in Prozent | ||
{{!-}} | {{!-}} | ||
{{!}} ARD | {{!}} ARD | ||
{{!}} <math>10</math> | {{!}} <math>10</math> | ||
{{!}} <div class="lueckentext-quiz"> '''10/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''7,69 | {{!}} <div class="lueckentext-quiz"> '''7,69()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} RTL | {{!}} RTL | ||
{{!}} <math>35</math> | {{!}} <math>35</math> | ||
{{!}} <div class="lueckentext-quiz"> '''35/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''35/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''26,92 | {{!}} <div class="lueckentext-quiz"> '''26,92()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} ProSieben | {{!}} ProSieben | ||
{{!}} <math>42</math> | {{!}} <math>42</math> | ||
{{!}} <div class="lueckentext-quiz"> '''42/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''42/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''32,31 | {{!}} <div class="lueckentext-quiz"> '''32,31()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} ZDF | {{!}} ZDF | ||
{{!}} <math>14</math> | {{!}} <math>14</math> | ||
{{!}} <div class="lueckentext-quiz"> '''14/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''14/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''10,77 | {{!}} <div class="lueckentext-quiz"> '''10,77()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} KabelEins | {{!}} KabelEins | ||
{{!}} <math>27</math> | {{!}} <math>27</math> | ||
{{!}} <div class="lueckentext-quiz"> '''27/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''27/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''20,77 | {{!}} <div class="lueckentext-quiz"> '''20,77()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} Eurosport | {{!}} Eurosport | ||
{{!}} <math>2</math> | {{!}} <math>2</math> | ||
{{!}} <div class="lueckentext-quiz"> '''2/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''2/130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''1,54 | {{!}} <div class="lueckentext-quiz"> '''1,54()''' </div> | ||
{{!-}} | {{!-}} | ||
! Gesamt | ! Gesamt | ||
{{!}} <div class="lueckentext-quiz"> '''130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''130()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''130/130()''' </div> | {{!}} <div class="lueckentext-quiz"> '''130/130()''' </div> | ||
{{!}} < | {{!}} <math>100{,}00</math> | ||
{{!)}} | {{!)}} | ||
| Zeile 260: | Zeile 214: | ||
{{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | {{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | ||
{{Lösung versteckt| 1= [[Datei: | {{Lösung versteckt| 1= [[Datei:Lösung-2.jpg|zentriert]]|2= Lösung |3= }} | ||
| 3= Arbeitsmethode | | 3= Arbeitsmethode | ||
| Zeile 267: | Zeile 221: | ||
{{Box | {{Box | ||
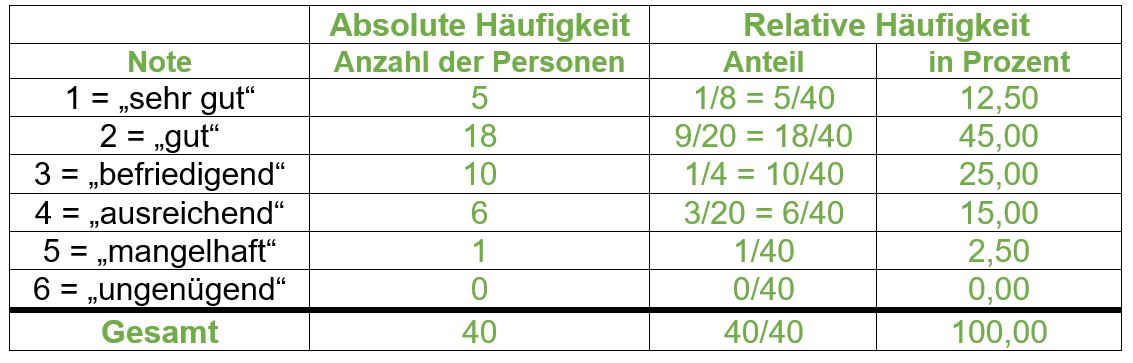
| 1= Aufgabe | | 1= Aufgabe 3: Hotelbewertung | ||
| 2= | | 2= | ||
| Zeile 289: | Zeile 243: | ||
! '''Anzahl der Personen''' | ! '''Anzahl der Personen''' | ||
! Anteil | ! Anteil | ||
! '''Prozent''' | ! '''in Prozent''' | ||
{{!-}} | {{!-}} | ||
{{!}} <math>1</math> = "sehr gut" | {{!}} <math>1</math> = "sehr gut" | ||
| Zeile 328: | Zeile 282: | ||
</div> | </div> | ||
{{Lösung versteckt| 1= [[Datei:Lösung | {{Lösung versteckt| 1=[[Datei:Lösung-3a.jpg|zentriert]] |2= Lösung |3= }} | ||
<br /> | <br /> | ||
| Zeile 344: | Zeile 298: | ||
! Anzahl der Personen | ! Anzahl der Personen | ||
! Anteil | ! Anteil | ||
! Prozent | ! in Prozent | ||
{{!-}} | {{!-}} | ||
{{!}} <math>1</math> = "sehr gut" | {{!}} <math>1</math> = "sehr gut" | ||
{{!}} <div class="lueckentext-quiz"> '''5()''' </div> | {{!}} <div class="lueckentext-quiz"> '''5()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''5/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''5/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''12,50 | {{!}} <div class="lueckentext-quiz"> '''12,50()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} <math>2</math> = "gut" | {{!}} <math>2</math> = "gut" | ||
{{!}} <div class="lueckentext-quiz"> '''18()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''18/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''18/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''45,00 | {{!}} <div class="lueckentext-quiz"> '''45,00()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} <math>3</math> = "befriedigend" | {{!}} <math>3</math> = "befriedigend" | ||
{{!}} <div class="lueckentext-quiz"> '''10()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''10/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''10/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''25,00 | {{!}} <div class="lueckentext-quiz"> '''25,00()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} <math>4</math> = "ausreichend" | {{!}} <math>4</math> = "ausreichend" | ||
{{!}} <div class="lueckentext-quiz"> '''6()''' </div> | {{!}} <div class="lueckentext-quiz"> '''6()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''6/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''6/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''15, | {{!}} <div class="lueckentext-quiz"> '''15,00()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} <math>5</math> = "mangelhaft" | {{!}} <math>5</math> = "mangelhaft" | ||
{{!}} <div class="lueckentext-quiz"> '''1()''' </div> | {{!}} <div class="lueckentext-quiz"> '''1()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''1/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''1/40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''2,50 | {{!}} <div class="lueckentext-quiz"> '''2,50()''' </div> | ||
{{!-}} | {{!-}} | ||
{{!}} <math>6</math> = "ungenügend" | {{!}} <math>6</math> = "ungenügend" | ||
{{!}} <div class="lueckentext-quiz"> '''0()''' </div> | {{!}} <div class="lueckentext-quiz"> '''0()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''0/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''0/40()''' </div> | ||
{{!}} < | {{!}} <math>0{,}00</math> | ||
{{!-}} | {{!-}} | ||
! Gesamt | ! Gesamt | ||
{{!}} <div class="lueckentext-quiz"> '''40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''40()''' </div> | ||
{{!}} <div class="lueckentext-quiz"> '''40/40()''' </div> | {{!}} <div class="lueckentext-quiz"> '''40/40()''' </div> | ||
{{!}} < | {{!}} <math>100{,}00</math> | ||
{{!)}} | {{!)}} | ||
| Zeile 387: | Zeile 341: | ||
{{Lösung versteckt| 1= [[Datei:Lösung- | {{Lösung versteckt| 1= [[Datei:Lösung-3b.jpg|zentriert]] |2= Lösung |3= }} | ||
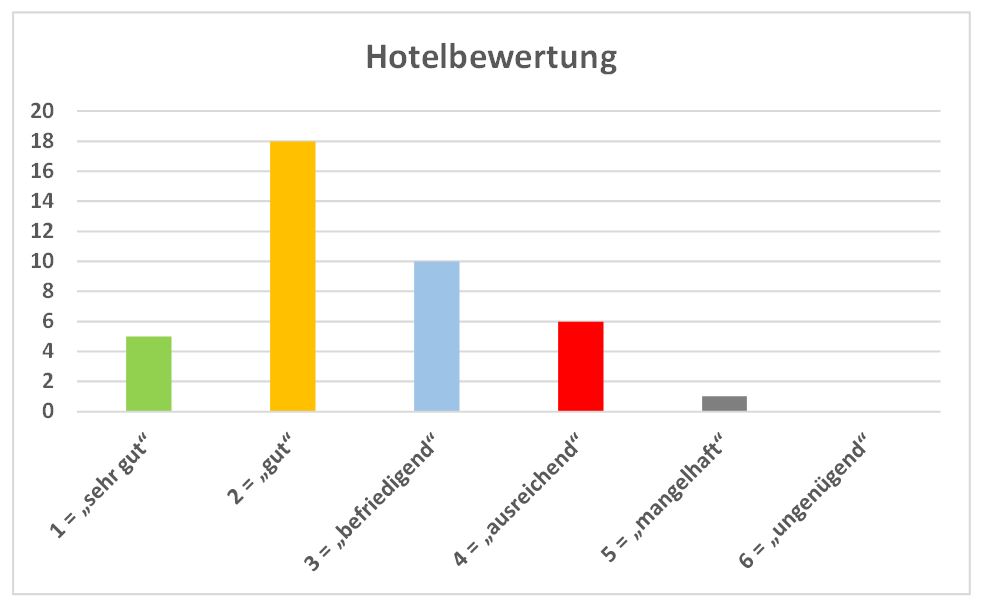
'''c)''' Zeichne ein Säulendiagramm, welches die absoluten Werte der Umfrage darstellt. | '''c)''' Zeichne ein Säulendiagramm, welches die absoluten Werte der Umfrage darstellt. | ||
| Zeile 393: | Zeile 347: | ||
{{Lösung versteckt| 1= [[Datei:Diagramm4-1.jpg|zentriert]] |2= Lösung |3= }} | {{Lösung versteckt| 1= [[Datei:Diagramm4-1.jpg|zentriert]] |2= Lösung |3= }} | ||
| 3= Arbeitsmethode | | 3= Arbeitsmethode | ||
| Farbe={{Farbe|grün|dunkel}} | }} | ||
{{Box | |||
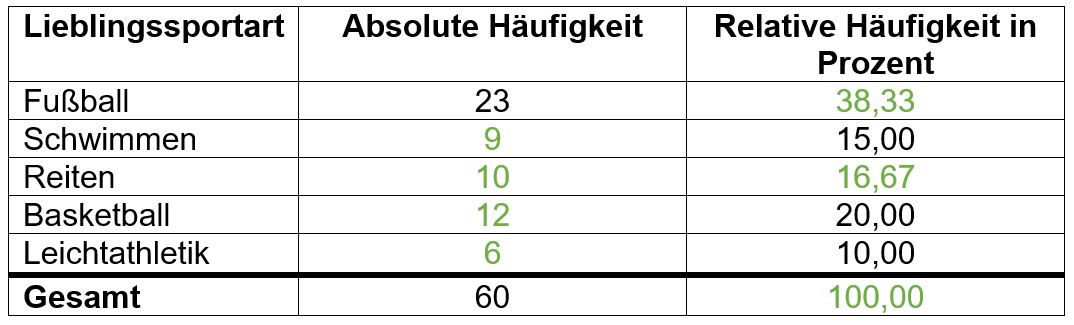
| 1= Aufgabe 4: Lieblingssportart | |||
| 2= Vervollständige die Tabelle: | |||
{{(!}} class="wikitable" | |||
! Lieblingssportart | |||
! Absolute Häufigkeit | |||
! Relative Häufigkeit in Prozent | |||
{{!-}} | |||
{{!}} Fußball | |||
{{!}} <math>23</math> | |||
{{!}} <div class="lueckentext-quiz"> '''38,33()''' </div> | |||
{{!-}} | |||
{{!}} Schwimmen | |||
{{!}} <div class="lueckentext-quiz"> '''9()''' </div> | |||
{{!}} <math>15{,}00</math> | |||
{{!-}} | |||
{{!}} Reiten | |||
{{!}} <div class="lueckentext-quiz"> '''10()''' </div> | |||
{{!}} <div class="lueckentext-quiz"> '''16,67()''' </div> | |||
{{!-}} | |||
{{!}} Basketball | |||
{{!}} <div class="lueckentext-quiz"> '''12()''' </div> | |||
{{!}} <math>20{,}00</math> | |||
{{!-}} | |||
{{!}} Leichtathletik | |||
{{!}} <div class="lueckentext-quiz"> '''6()''' </div> | |||
{{!}} <math>10{,}00</math> | |||
{{!-}} | |||
! Gesamt | |||
{{!}} <math>60</math> | |||
{{!}} <div class="lueckentext-quiz"> '''100,00()''' </div> | |||
{{!)}} | |||
{{Lösung versteckt| 1= Runde die berechnete Prozentzahl auf zwei Nachkommastellen genau. |2= Prozentzahl runden |3= }} | |||
{{Lösung versteckt| 1= [[Datei:Lösung-4.jpg|zentriert]] |2= Lösung |3= }} | |||
| 3= Arbeitsmethode | |||
| Farbe={{Farbe|grün|dunkel}} | |||
}} | }} | ||
| Zeile 429: | Zeile 424: | ||
<div class="lueckentext-quiz">Max und Julian haben insgesamt '''80()''' Fahrzeuge gezählt.</div> | <div class="lueckentext-quiz">Max und Julian haben insgesamt '''80()''' Fahrzeuge gezählt.</div> | ||
{{Lösung versteckt| 1= Aus dem Aufgabentext weißt du, dass <math>8</math> Busse <math>10</math> % aller Fahrzeuge sind. Für die anderen Fahrzeuganzahlen nutzt du den Dreisatz: | {{Lösung versteckt| 1= Aus dem Aufgabentext weißt du, dass <math>8</math> Busse <math>10</math> % aller Fahrzeuge (F) sind. Für die anderen Fahrzeuganzahlen nutzt du den Dreisatz: | ||
<math>10</math> % <math>= | <math>10</math> % <math>= 8</math> F | ||
<math> 1</math> % <math>= | <math> 1</math> % <math>= 8</math> F <math> : 10</math> % | ||
<math> x</math> % <math>= | <math> x</math> % <math>= 8</math> F <math> : 10</math> % <math>\cdot x</math> % | ||
|2= Tipp Fahrzeuganzahl |3= }} | |2= Tipp Fahrzeuganzahl |3= }} | ||
| Zeile 446: | Zeile 441: | ||
| Farbe={{Farbe|grün|dunkel}} | | Farbe={{Farbe|grün|dunkel}} | ||
}} | }} | ||
==Zufallsexperimente== | ==Zufallsexperimente== | ||
| Zeile 455: | Zeile 449: | ||
Die Wahrscheinlichkeit berechnet sich dann aus <math>\tfrac{\text{Anzahl der Ergebnisse zu gefragten Ereignis}}{\text{Anzahl aller möglichen Ergebnisse}} </math>. | Die Wahrscheinlichkeit berechnet sich dann aus <math>\tfrac{\text{Anzahl der Ergebnisse zu gefragten Ereignis}}{\text{Anzahl aller möglichen Ergebnisse}} </math>. | ||
Anders als bei der relativen Häufigkeit, | Anders als bei der relativen Häufigkeit, geht es hier nicht um die Erfassung von Daten, sondern um die Berechnung von Wahrscheinlichkeiten. | Merksatz}} | ||
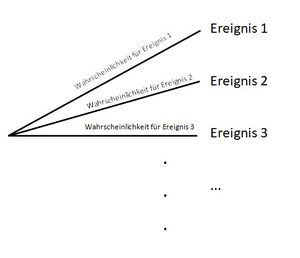
{{Box | Baumdiagramme| | {{Box | Baumdiagramme| | ||
| Zeile 469: | Zeile 459: | ||
{{Box | Aufgabe 6: Klassendienste | | {{Box | Aufgabe 6: Klassendienste | | ||
In einer Klasse sind 14 Jungen und 13 Mädchen. Es werden Beauftragte für verschiedene Klassendienste gelost. | In einer Klasse sind <math>14</math> Jungen und <math>13</math> Mädchen. Es werden Beauftragte für verschiedene Klassendienste gelost. | ||
'''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | '''a)''' Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist? | ||
| Zeile 488: | Zeile 478: | ||
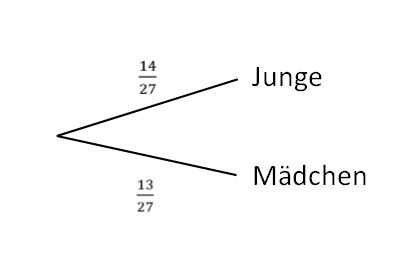
[[Datei:Baumdiagramm A1 a.jpg|zentriert]] | [[Datei:Baumdiagramm A1 a.jpg|zentriert]] | ||
Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt also bei <math>\tfrac{14}{27}</math> bzw. bei ungefähr <math>51{,}85 | Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt also bei <math>\tfrac{14}{27}</math> bzw. bei ungefähr <math>51{,}85</math> %. | ||
|2= Lösung |3= Lösung}} | |2= Lösung |3= Lösung}} | ||
| Zeile 503: | Zeile 493: | ||
3. Die Lehrperson wird gelost. | 3. Die Lehrperson wird gelost. | ||
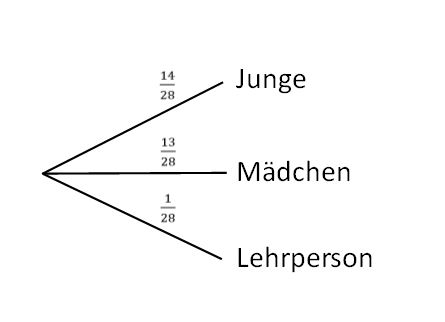
Auch hier ergeben sich die Wahrscheinlichen aus den relativen Häufigkeiten. Hierbei muss allerdings darauf geachtet werden, dass nicht nur die Anzahl der Schülerinnen und Schüler als gesamte Menge betrachtet wird, sondern auch die Lehrperson hinzu addiert wird. Es stehen also insgesamt 28 Personen zur Auswahl. Das Baumdiagramm sieht so aus: | Auch hier ergeben sich die Wahrscheinlichen aus den relativen Häufigkeiten. Hierbei muss allerdings darauf geachtet werden, dass nicht nur die Anzahl der Schülerinnen und Schüler als gesamte Menge betrachtet wird, sondern auch die Lehrperson hinzu addiert wird. Es stehen also insgesamt <math>28</math> Personen zur Auswahl. Das Baumdiagramm sieht so aus: | ||
[[Datei:Baumdiagramm A1 b.jpg|zentriert]] | [[Datei:Baumdiagramm A1 b.jpg|zentriert]] | ||
Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math> bzw. bei <math>3{,}57 | Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei <math>\tfrac{1}{28}</math> bzw. bei <math>3{,}57</math> %. | ||
|2= Lösung |3= Lösung}} | |2= Lösung |3= Lösung}} | ||
| Zeile 561: | Zeile 551: | ||
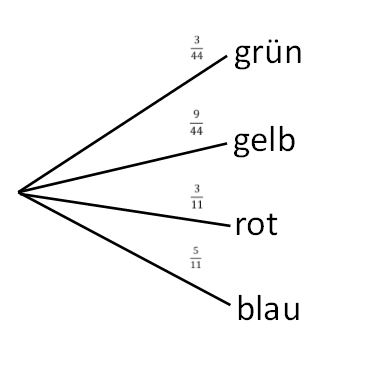
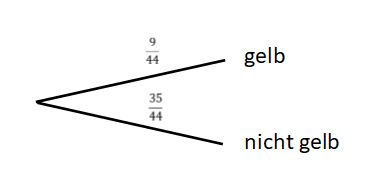
Rechne das nun in Prozent um: | Rechne das nun in Prozent um: | ||
<math>\tfrac{9}{44} \approx 0{,}2045 = 20{,}45 | <math>\tfrac{9}{44} \approx 0{,}2045 = 20{,}45</math> %. | ||
Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei <math>20{,}45 | Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei <math>20{,}45</math> %. | ||
|2= Lösung |3= Lösung }} | |2= Lösung |3= Lösung }} | ||
| Zeile 602: | Zeile 592: | ||
Nun rechnet man die Brüche in Prozent um: | Nun rechnet man die Brüche in Prozent um: | ||
Wahrscheinlichkeit zu verlieren: <math>\tfrac{5}{11} \approx 0{,}4545 = 45{,}45 | Wahrscheinlichkeit zu verlieren: <math>\tfrac{5}{11} \approx 0{,}4545 = 45{,}45</math> %. | ||
Wahrscheinlichkeit zu gewinnen: <math>100 %-45{,}45%=54{,}55 | Wahrscheinlichkeit zu gewinnen: <math>100</math> % <math>-45{,}45</math> % <math>=54{,}55</math> %. | ||
Die Wahrscheinlichkeit, zu gewinnen liegt bei <math>54{,}55 | Die Wahrscheinlichkeit, zu gewinnen liegt bei <math>54{,}55</math> %, die zu verlieren bei <math>45{,}45</math> %. Die Aussage stimmt also. | ||
|2= Lösung |3= Lösung }} | |2= Lösung |3= Lösung }} | ||
| Arbeitsmethode }} | | Arbeitsmethode }} | ||
{{Box | Pfadadditionsregel | | |||
Gehören zu einem Ereignis mehrere Pfade in einem Baumdiagramm, dann erhält man die Wahrscheinlichkeit des Ereignisses, indem man die Pfadwahrscheinlichkeiten der einzelnen zu dem Ereignis gehörenden Ergebnisse addiert. | |||
| Merksatz}} | |||
{{Box |Pfadmultiplikationsregel| | {{Box |Pfadmultiplikationsregel| | ||
| Zeile 620: | Zeile 613: | ||
<math>P(\text{Ereignis A} | \text{Ereignis B})= \text{Wahrscheinlichkeit A} \cdot \text{Wahrscheinlichkeit B} </math> | <math>P(\text{Ereignis A} | \text{Ereignis B})= \text{Wahrscheinlichkeit A} \cdot \text{Wahrscheinlichkeit B} </math> | ||
<math>*</math> Diese Schreibweise bedeutet, dass erst Ereignis A und danach Ereignis B eintritt. | |||
* Diese Schreibweise | |||
| Merksatz}} | | Merksatz}} | ||
| Zeile 677: | Zeile 669: | ||
| Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | | Arbeitsmethode | Farbe={{Farbe|grün|dunkel}} }} | ||
==Laplace-Experimente== | ==Laplace-Experimente== | ||
| Zeile 685: | Zeile 676: | ||
Bei <math>n</math> Ergebnissen ist die Wahrscheinlichkeit in einem Laplace-Experiment für jedes Ergebnis <math>\tfrac{1}{n}</math>. | Bei <math>n</math> Ergebnissen ist die Wahrscheinlichkeit in einem Laplace-Experiment für jedes Ergebnis <math>\tfrac{1}{n}</math>. | ||
| Merksatz}} | | Merksatz}} | ||
| Zeile 714: | Zeile 700: | ||
Für das Ereignis eine Dame zu ziehen gibt es insgesamt <math>4</math> Karten. Also <math>4</math> mögliche Ergebnisse, dessen Wahrscheinlichkeiten nach der Summenregel addiert werden können. | Für das Ereignis eine Dame zu ziehen gibt es insgesamt <math>4</math> Karten. Also <math>4</math> mögliche Ergebnisse, dessen Wahrscheinlichkeiten nach der Summenregel addiert werden können. | ||
<math> P(\text{Dame wird gezogen}) = \tfrac{1}{32} + \tfrac{1}{32} + \tfrac{1}{32} + \tfrac{1}{32} = 4 \cdot \tfrac{1}{32} = \tfrac{4}{32} = \tfrac{1}{8} </math>|2=Lösung a)|3=Lösung}} | <math> P(\text{Dame wird gezogen}) = \tfrac{1}{32} + \tfrac{1}{32} + \tfrac{1}{32} + \tfrac{1}{32} = 4 \cdot \tfrac{1}{32} = \tfrac{4}{32} = \tfrac{1}{8} </math> | ||
Die Wahrscheinlichkeit eine Dame zu ziehen beträgt somit <math>\tfrac{1}{8}</math>. |2=Lösung a)|3=Lösung}} | |||
{{Lösung versteckt|1='''b)''' Es gibt insgesamt <math>8</math> Kreuz-Karten. | {{Lösung versteckt|1='''b)''' Es gibt insgesamt <math>8</math> Kreuz-Karten. | ||
Also gilt mit der Summenregel: | Also gilt mit der Summenregel: | ||
<math>P(\text{Kreuz-Karte wird gezogen})=\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}=8\cdot\tfrac{1}{32}=\tfrac{8}{32}=\tfrac{1}{4}</math> |2=Lösung b)|3=Lösung}} | <math>P(\text{Kreuz-Karte wird gezogen})=\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}+\tfrac{1}{32}=8\cdot\tfrac{1}{32}=\tfrac{8}{32}=\tfrac{1}{4}</math> | ||
Die Wahrscheinlichkeit eine Kreuz-Karte zu ziehen beträgt somit <math>\tfrac{1}{4}</math>.|2=Lösung b)|3=Lösung}} | |||
{{Lösung versteckt|1='''c)''' Es gibt <math>8</math> Pik und <math>8</math> Kreuz-Karten, also insgesamt <math>16</math> schwarze Karten. | {{Lösung versteckt|1='''c)''' Es gibt <math>8</math> Pik und <math>8</math> Kreuz-Karten, also insgesamt <math>16</math> schwarze Karten. | ||
Also gilt mit der Summenregel: | Also gilt mit der Summenregel: | ||
<math> P(\text{Schwarze Karte wird gezogen})=16\cdot\tfrac{1}{32}=\tfrac{16}{32}=\tfrac{1}{2} </math>|2=Lösung c)|3=Lösung}} | <math> P(\text{Schwarze Karte wird gezogen})=16\cdot\tfrac{1}{32}=\tfrac{16}{32}=\tfrac{1}{2} </math> | ||
Die Wahrscheinlichkeit eine schwarze Karte zu ziehen beträgt somit <math>\tfrac{1}{2}</math>.|2=Lösung c)|3=Lösung}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
| Zeile 754: | Zeile 746: | ||
Da unter den Steinen nur einmal der Buchstabe D vorhanden ist gilt: | Da unter den Steinen nur einmal der Buchstabe D vorhanden ist gilt: | ||
<math>P(\text{D wird gezogen})=\tfrac{1}{13}</math>. |2=Lösung a)|3=Lösung}} | <math>P(\text{D wird gezogen})=\tfrac{1}{13}</math>. | ||
Die Wahrscheinlichkeit den Buchstaben D zu ziehen beträgt somit <math>\tfrac{1}{13}</math>.|2=Lösung a)|3=Lösung}} | |||
{{Lösung versteckt|1='''b)''' Es gibt zwei Spielsteine mit dem Buchstaben N, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. | {{Lösung versteckt|1='''b)''' Es gibt zwei Spielsteine mit dem Buchstaben N, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. | ||
| Zeile 760: | Zeile 754: | ||
Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der beiden möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der beiden möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | ||
Es gilt also: <math>P(\text{N wird gezogen})=\tfrac{1}{13}+\tfrac{1}{13}=\tfrac{2}{13}</math>|2=Lösung b)|3=Lösung}} | Es gilt also: <math>P(\text{N wird gezogen})=\tfrac{1}{13}+\tfrac{1}{13}=\tfrac{2}{13}</math> | ||
Die Wahrscheinlichkeit den Buchstaben N zu ziehen beträgt somit <math>\tfrac{2}{13}</math>.|2=Lösung b)|3=Lösung}} | |||
{{Lösung versteckt|1='''c)''' Es gibt insgesamt <math>3</math> Spielsteine mit dem Buchstaben O, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der drei möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | {{Lösung versteckt|1='''c)''' Es gibt insgesamt <math>3</math> Spielsteine mit dem Buchstaben O, die jeweils mit einer Wahrscheinlichkeit von <math>\tfrac{1}{13}</math> gezogen werden. Wegen der Summenregel für Laplace-Experimente können die Wahrscheinlichkeiten der drei möglichen Ergebnisse bzw. Spielsteine für das Ereignis addiert werden. | ||
Es gilt also: <math>P(\text{O wird gezogen})=\tfrac{1}{13}+\tfrac{1}{13}+\tfrac{1}{13}= \tfrac{3}{13}</math>|2=Lösung c) |3=Lösung}} | Es gilt also: <math>P(\text{O wird gezogen})=\tfrac{1}{13}+\tfrac{1}{13}+\tfrac{1}{13}= \tfrac{3}{13}</math> | ||
Die Wahrscheinlichkeit den Buchstaben O zu ziehen beträgt somit <math>\tfrac{3}{13}</math>.|2=Lösung c) |3=Lösung}} | |||
{{Lösung versteckt|1='''d)''' Insgesamt gibt es einen Spielstein mit A und drei mit einem O. Die restlichen Vokale sind nicht vorhanden. | {{Lösung versteckt|1='''d)''' Insgesamt gibt es einen Spielstein mit A und drei mit einem O. Die restlichen Vokale sind nicht vorhanden. | ||
Somit folgt mit der Summenregel: | Somit folgt mit der Summenregel: | ||
<math>P(\text{Vokal wird gezogen})=\tfrac{1}{13}+\tfrac{3}{13}=\tfrac{4}{13}</math>|2=Lösung d)|3=Lösung}} | <math>P(\text{Vokal wird gezogen})=\tfrac{1}{13}+\tfrac{3}{13}=\tfrac{4}{13}</math> | ||
Die Wahrscheinlichkeit einen Vokal zu ziehen beträgt somit <math>\tfrac{4}{13}</math>.|2=Lösung d)|3=Lösung}} | |||
| Arbeitsmethode | Farbe={{Farbe|orange}} }} | | Arbeitsmethode | Farbe={{Farbe|orange}} }} | ||
| Zeile 776: | Zeile 776: | ||
Es wird mit zwei Würfeln gewürfelt. Wie hoch ist die Wahrscheinlichkeit, dass… | Es wird mit zwei Würfeln gewürfelt. Wie hoch ist die Wahrscheinlichkeit, dass… | ||
'''a)''' …ein Pasch (Zweimal die | '''a)''' …ein Pasch (Zweimal die gleiche Zahl, z.B. {1,1}) gewürfelt wird? | ||
| Zeile 786: | Zeile 786: | ||
{{Lösung versteckt|1=Primzahl: ganze Zahl, die größer als <math>1</math> und nur durch <math>1</math> und sich selbst teilbar ist. | {{Lösung versteckt|1=Primzahl: ganze Zahl, die größer als <math>1</math> und nur durch <math>1</math> und sich selbst teilbar ist. | ||
{{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die <math>2, 3, 5, 7, 11</math>. Überlege dir jetzt, mit welchen der möglichen Zahlenkombinationen von zwei Würfeln man mithilfe der Addition auf diese Primzahlen kommt.|2=Tipp 2 |3=Tipp}} | {{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die <math>2</math>, <math>3</math>, <math>5</math>, <math>7</math>, <math>11</math>. Überlege dir jetzt, mit welchen der möglichen Zahlenkombinationen von zwei Würfeln man mithilfe der Addition auf diese Primzahlen kommt.|2=Tipp 2 |3=Tipp}} | ||
|2=Tipp |3=Tipp}} | |2=Tipp |3=Tipp}} | ||
| Zeile 792: | Zeile 792: | ||
{{Lösung versteckt|1=Mit jeder Zahl kann ein Pasch geworfen werden. Es gibt demnach insgesamt sechs verschiedene Pasche. Da die jeweiligen Zahlen identisch sind, ist die Reihenfolge nicht zu betrachten. | {{Lösung versteckt|1=Mit jeder Zahl kann ein Pasch geworfen werden. Es gibt demnach insgesamt sechs verschiedene Pasche. Da die jeweiligen Zahlen identisch sind, ist die Reihenfolge nicht zu betrachten. | ||
Das Ereignis ist also: <math>E= | Das Ereignis ist also: <math>E=\lbrace\lbrace1,1\rbrace;\lbrace2,2\rbrace;\lbrace3,3\rbrace;\lbrace4,4\rbrace;\lbrace5,5\rbrace;\lbrace6,6\rbrace\rbrace</math> | ||
Es gibt somit insgesamt <math>6</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | Es gibt somit insgesamt <math>6</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | ||
| Zeile 801: | Zeile 801: | ||
{{Lösung versteckt|1= Es gibt <math>3</math> unterschiedliche Kombinationen von Zahlen, deren Differenz <math>3</math> beträgt. Die 4 und 1, die 5 und 2 & die 6 und 3. Die einzelnen Kombinationen können jeweils in zwei unterschiedlichen Reihenfolgen geworfen werden. | {{Lösung versteckt|1= Es gibt <math>3</math> unterschiedliche Kombinationen von Zahlen, deren Differenz <math>3</math> beträgt. Die 4 und 1, die 5 und 2 & die 6 und 3. Die einzelnen Kombinationen können jeweils in zwei unterschiedlichen Reihenfolgen geworfen werden. | ||
Das Ereignis ist also: <math>E = | Das Ereignis ist also: <math>E = \lbrace \lbrace1,4\rbrace; \lbrace4,1\rbrace; \lbrace2,5\rbrace; \lbrace5,2\rbrace; \lbrace3,6\rbrace; \lbrace6,3\rbrace \rbrace</math> | ||
Es gibt somit insgesamt <math>6</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | Es gibt somit insgesamt <math>6</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | ||
| Zeile 808: | Zeile 808: | ||
<math>P(E)=\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}=6\cdot\tfrac{1}{36}=\tfrac{6}{36}= \tfrac{1}{6}</math>|2=Lösung b) |3=Lösung}} | <math>P(E)=\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}+\tfrac{1}{36}=6\cdot\tfrac{1}{36}=\tfrac{6}{36}= \tfrac{1}{6}</math>|2=Lösung b) |3=Lösung}} | ||
{{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die <math>2, 3, 5, 7, 11</math>. Es gibt <math>8</math> unterschiedliche Kombinationen von Zahlen, deren Summe eine dieser Primzahlen ist. Die 1+1, die 1+2, die 1+4, die 1+6, die 2+3, die 2+5, die 3+4 und die 5+6. Die einzelnen Kombinationen können jeweils in zwei unterschiedlichen Reihenfolgen geworfen werden, außer das 1er-Pasch. | {{Lösung versteckt|1=Die Primzahlen, die mit zwei Würfeln erreicht werden können, sind die <math>2</math>, <math>3</math>, <math>5</math>, <math>7</math>, <math>11</math>. Es gibt <math>8</math> unterschiedliche Kombinationen von Zahlen, deren Summe eine dieser Primzahlen ist. Die 1+1, die 1+2, die 1+4, die 1+6, die 2+3, die 2+5, die 3+4 und die 5+6. Die einzelnen Kombinationen können jeweils in zwei unterschiedlichen Reihenfolgen geworfen werden, außer das 1er-Pasch. | ||
Das Ereignis ist also: <math>E = | Das Ereignis ist also: <math>E = \lbrace \lbrace1,1\rbrace; \lbrace1,2\rbrace; \lbrace2,1\rbrace; \lbrace1,4\rbrace; \lbrace4,1\rbrace; \lbrace1,6\rbrace; \lbrace6,1\rbrace; \lbrace2,3\rbrace; \lbrace3,2\rbrace; \lbrace2,5\rbrace; \lbrace5,2\rbrace; \lbrace3,4\rbrace; \lbrace4,3\rbrace; \lbrace5,6\rbrace; \lbrace6,5\rbrace \rbrace</math> | ||
Es gibt somit insgesamt <math>15</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | Es gibt somit insgesamt <math>15</math> verschiedene Ergebnisse für das Ereignis. Die einzelnen Ergebnisse haben alle eine Wahrscheinlichkeit von <math>\tfrac{1}{36}</math>, da es mit zwei Würfeln insgesamt <math>36</math> verschiedene Zahlenkombinationen gibt. | ||
| Zeile 845: | Zeile 845: | ||
Da der Würfel sechs Zahlen aufweist, beträgt die Wahrscheinlichkeit für jede einzelne Zahl <math>\tfrac{1}{6}</math> und somit gilt mit der Summenregel, da Markus drei der sechs Zahlen würfeln kann: | Da der Würfel sechs Zahlen aufweist, beträgt die Wahrscheinlichkeit für jede einzelne Zahl <math>\tfrac{1}{6}</math> und somit gilt mit der Summenregel, da Markus drei der sechs Zahlen würfeln kann: | ||
<math>P(\text{Markus würfelt eine | <math>P(\text{Markus würfelt eine 1, 2 oder 3})=\tfrac{1}{6}+\tfrac{1}{6}+\tfrac{1}{6}=\tfrac{3}{6}=\tfrac{1}{2}</math> | ||
| Zeile 852: | Zeile 852: | ||
Da Julia nur zwei der sechs Zahlen würfeln kann, gilt: | Da Julia nur zwei der sechs Zahlen würfeln kann, gilt: | ||
<math>P(\text{Julia würfelt eine | <math>P(\text{Julia würfelt eine 5 oder 6})=\tfrac{1}{6}+\tfrac{1}{6}=\tfrac{2}{6}=\tfrac{1}{3}</math> | ||
| Zeile 863: | Zeile 863: | ||
Dann kann Julia mit den Zahlen 4, 5 und 6 beim darauffolgenden Zug ins Haus kommen. | Dann kann Julia mit den Zahlen 4, 5 und 6 beim darauffolgenden Zug ins Haus kommen. | ||
<math>P(\text{Julia würfelt eine | <math>P(\text{Julia würfelt eine 4, 5 oder 6})=\tfrac{1}{6}+\tfrac{1}{6}+\tfrac{1}{6}=3 \cdot\tfrac{1}{6}=\tfrac{3}{6}=\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
| Zeile 871: | Zeile 871: | ||
Dann kann Julia mit den Zahlen 3, 4 und 5 beim darauffolgenden Zug ins Haus kommen: | Dann kann Julia mit den Zahlen 3, 4 und 5 beim darauffolgenden Zug ins Haus kommen: | ||
<math>P(\text{Julia würfelt eine | <math>P(\text{Julia würfelt eine 3, 4 oder 5})=3 \cdot\tfrac{1}{6}=\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
| Zeile 879: | Zeile 879: | ||
Dann kann Julia mit den Zahlen 2, 3 und 4 beim darauffolgenden Zug ins Haus kommen: | Dann kann Julia mit den Zahlen 2, 3 und 4 beim darauffolgenden Zug ins Haus kommen: | ||
<math>P(\text{Julia würfelt eine | <math>P(\text{Julia würfelt eine 2, 3 oder 4})=3 \cdot\tfrac{1}{6}=\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
| Zeile 887: | Zeile 887: | ||
Dann kann Julia mit den Zahlen 1, 2 und 3 beim darauffolgenden Zug ins Haus kommen: | Dann kann Julia mit den Zahlen 1, 2 und 3 beim darauffolgenden Zug ins Haus kommen: | ||
<math>P(\text{Julia würfelt eine | <math>P(\text{Julia würfelt eine 1, 2 oder 3})=3 \cdot\tfrac{1}{6}=\tfrac{1}{2}</math> | ||
Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | Die Wahrscheinlichkeit beim nächsten Zug ins Haus zu kommen beträgt dann sowohl bei Markus als auch bei Julia <math>\tfrac{1}{2}</math>. | ||
Aktuelle Version vom 14. Dezember 2020, 20:19 Uhr
Absolute und relative Häufigkeit
Zufallsexperimente
Laplace-Experimente