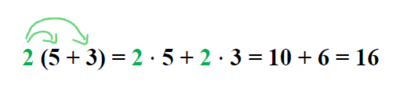Digitale Werkzeuge in der Schule/Fit für VERA-8/Terme: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 441: | Zeile 441: | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Wir suchen die passende binomische Formel für den Term <math> 9x^2-6xy+y^2 </math>. | Wir suchen die passende binomische Formel für den Term <math> 9x^2-6xy+y^2 </math>. | ||
Die Anzahl der Summanden bzw. Minuenden geben uns Auskunft darüber, welche bin. Formel wir anwenden können. In diesem Fall haben wir '''zwei Summanden''' und '''einen Minuenden'''. Dies stimmt mit der '''2. binomischen Formel''' überein: | Die Anzahl der Summanden bzw. Minuenden geben uns Auskunft darüber, welche bin. Formel wir anwenden können. In diesem Fall haben wir '''zwei Summanden''' und '''einen Minuenden'''. Dies stimmt mit der '''2. binomischen Formel''' überein: <br /> | ||
<math>( | <math>(a-b)^2 = a^2-2ab+b^2 </math>. Unsere binomische Formel hat also die Form <math>(a-b)^2 </math>. | ||
Nun müssen wir noch a und b herausfinden. Wir wissen <math> a^2 = 9x^2 </math> und <math> b^2 = y^2 </math>. | Nun müssen wir noch a und b herausfinden. Wir wissen, dass <math> a^2 = 9x^2 </math> und <math> b^2 = y^2 </math>. | ||
Nun ziehen wir aus diesen Ausdrücken die Wurzel, um a und b zu erhalten: | |||
<math> a = \sqrt{a^2} = \sqrt{9x^2} = 3x </math> und <math> b = \sqrt{b^2} = \sqrt{y^2} = y </math>. | <math> a = \sqrt{a^2} = \sqrt{9x^2} = 3x </math> und <math> b = \sqrt{b^2} = \sqrt{y^2} = y </math>. | ||
Also lautet die binomische Formel <math> (3x-y)^2 </math>. | Also lautet die binomische Formel <math> (3x-y)^2 </math>. | ||
Probe: <math> ({\color{green}3x}-{\color{blue}y})^2 = {\color{green}(3x)}^2-2 \cdot {\color{green}3x}{\color{blue}y}+{\color{blue}y}^2 = 9x^2-6xy+y^2 </math>. | Probe: <math> ({\color{green}3x}-{\color{blue}y})^2 = {\color{green}(3x)}^2-2 \cdot {\color{green}3x}{\color{blue}y}+{\color{blue}y}^2 = 9x^2-6xy+y^2 </math>. | ||
Das Vorgehen für die erste und dritte binomische Formel erfolgt sehr ähnlich. |2=Beispiel|3=Beispiel verbergen | Das Vorgehen für die erste und dritte binomische Formel erfolgt sehr ähnlich. |2=Beispiel|3=Beispiel verbergen}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
* Bei '''drei Summanden''' wendest du die '''1. binomische Formel''' an. | * Bei '''drei Summanden''' wendest du die '''1. binomische Formel''' an. | ||
* Bei '''zwei Summanden und einem Minuenden''' wendest du die '''2. binomische Formel''' an. | * Bei '''zwei Summanden und einem Minuenden''' wendest du die '''2. binomische Formel''' an. | ||
* Bei '''einem Summanden und einem Minuenden''' wendest du die '''3. binomische Formel''' an.|2=Tipp 2|3=Tipp ausblenden}} | * Bei '''einem Summanden und einem Minuenden''' wendest du die '''3. binomische Formel''' an.|2=Tipp 2|3=Tipp ausblenden}}| 3=Arbeitsmethode}} | ||
{{Box | 1=Aufgabe 3: Warum ist das so?| 2= | {{Box | 1=Aufgabe 3: Warum ist das so?| 2= | ||
Version vom 5. Dezember 2020, 10:19 Uhr
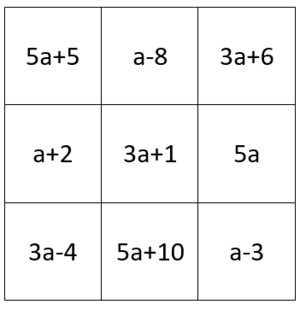
1) Terme zusammenfassen
Einführung
Aufgaben
2) Terme ausmultiplizieren und faktorisieren
Terme ausmultiplizieren
Aufgabe
Terme faktorisieren
Aufgabe
Weitere Aufgaben zum Ausmultiplizieren und Faktorisieren
3) Binomische Formeln
Was sind die binomischen Formeln?
Herleitung der binomischen Formeln
Beispiele
Aufgaben