Digitale Werkzeuge in der Schule/Fit für VERA-8/Stochastik: Unterschied zwischen den Versionen
Aus ZUM Projektwiki
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| Zeile 503: | Zeile 503: | ||
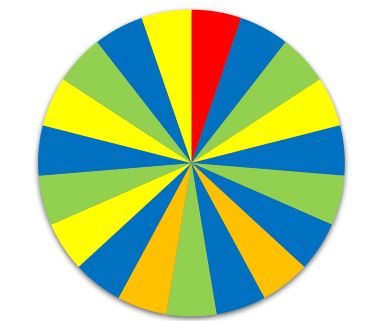
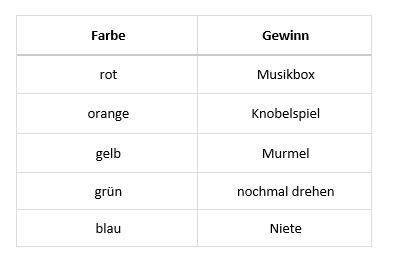
Bei eurem Schulfest gibt es eine Tombola. Es geht darum, aus einem Glas eine Kugel zu ziehen. Bevor du ohne Hinschauen ziehen darfst, wird dir einmal der Inhalt des Glases gezeigt. Du zählst die Kugeln. Außerdem steht ein Schild neben der Urne (Abbildung 2). Du kannst auf die Bilder klicken, um sie in vergrößerter Form zu sehen. | Bei eurem Schulfest gibt es eine Tombola. Es geht darum, aus einem Glas eine Kugel zu ziehen. Bevor du ohne Hinschauen ziehen darfst, wird dir einmal der Inhalt des Glases gezeigt. Du zählst die Kugeln. Außerdem steht ein Schild neben der Urne (Abbildung 2). Du kannst auf die Bilder klicken, um sie in vergrößerter Form zu sehen. | ||
[[Datei:Urne A2 1.jpg|mini| | [[Datei:Urne A2 1.jpg|mini|links|Abbildung 1]][[Datei:Plakat.jpg|mini|zentriert|Abbildung 2]] | ||
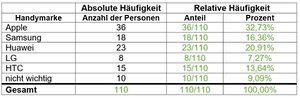
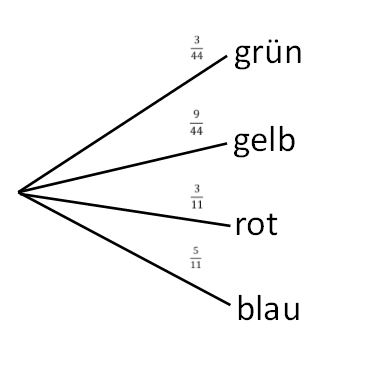
{{Lösung versteckt| 1= Es sind 20 blaue | {{Lösung versteckt| 1= Es sind 20 blaue, 12 rote, 9 gelbe und 3 grüne Kugeln. |2=Hilfe, falls du die Farben nicht unterscheiden kannst.|3=Hilfe, falls du die Farben nicht unterscheiden kannst.}} | ||
Nun ziehst du ohne hinzuschauen eine Kugel. | Nun ziehst du ohne hinzuschauen eine Kugel. | ||
'''a)''' Wie groß ist die Wahrscheinlichkeit, dass du einen Stift gewinnst (gelbe Kugel)? Gib die Lösung in Prozent an. | '''a)''' Wie groß ist die Wahrscheinlichkeit, dass du einen Stift gewinnst (gelbe Kugel)? Gib die Lösung in Prozent an. Runde das Ergebnis auf 2 Nachkommastellen. | ||
{{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}} | {{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}} | ||
| Zeile 547: | Zeile 547: | ||
|2= Lösung |3= Lösung }} | |2= Lösung |3= Lösung }} | ||
'''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? | '''b)''' Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Begründe. | ||
{{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}} | {{Lösung versteckt| 1= Berechne zunächst die einzelnen Wahrscheinlichkeiten.Gibt die Lösung wieder in Prozent an. Runde das Ergebnis auf 2 Nachkommastellen. {{Lösung versteckt| 1= Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?|2=Tipp|3=Tipp}}|2=Tipp|3=Tipp}} | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 598: | Zeile 598: | ||
[[Datei:Pfadregel Multiplikation.jpg|zentriert]] | [[Datei:Pfadregel Multiplikation.jpg|zentriert]] | ||
Die Wahrscheinlichkeit von (Ereignis A <math>\mid</math> Ereignis B) ist dann: | Die Wahrscheinlichkeit von (Ereignis A <math>\mid</math> Ereignis B)* ist dann: | ||
<math>P(\text{Ereignis A} | \text{Ereignis B})= \text{Wahrscheinlichkeit A} \cdot \text{Wahrscheinlichkeit B} </math> | <math>P(\text{Ereignis A} | \text{Ereignis B})= \text{Wahrscheinlichkeit A} \cdot \text{Wahrscheinlichkeit B} </math> | ||
* Diese Schreibweise heißt, dass das Ereignis B bereits bekannt ist. Man möchte nun schauen, wie wahrscheinlich es ist, dass davor bereits Ereignis A eingetreten ist. Man sagt dann: "Die Wahrscheinlichkeit für Ereignis A unter der Voraussetzung, dass Ereignis B eingetreten ist." | |||
| Merksatz}} | | Merksatz}} | ||
| Zeile 615: | Zeile 617: | ||
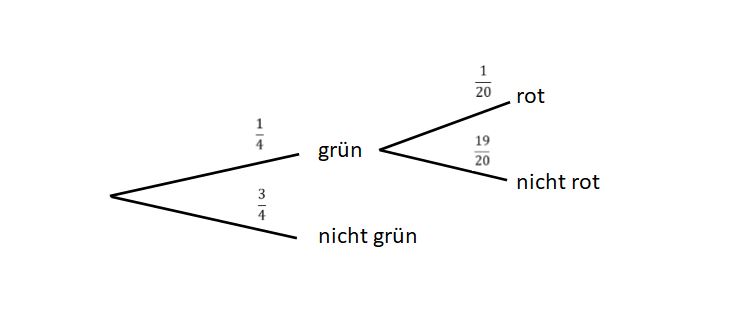
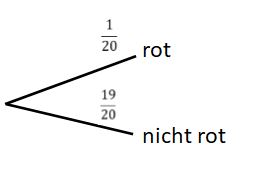
'''a)''' Du hast einmal gedreht und landest auf einem grünen Feld. Du darfst also | '''a)''' Du hast einmal gedreht und landest auf einem grünen Feld. Du darfst also noch einmal drehen. Beim zweiten Drehen landest du auf dem roten Feld. Wie groß ist die Wahrscheinlichkeit, dass diese beiden Fälle direkt hintereinander eintreten? | ||
{{Lösung versteckt| 1= Wie groß ist die Wahrscheinlichkeit | {{Lösung versteckt| 1= Wie groß ist die Wahrscheinlichkeit noch einmal drehen zu dürfen? Zeichne hierzu ein Baumdiagramm. {{Lösung versteckt| 1= Nun kannst du das Baumdiagramm fortführen. Verwende die Pfadmultiplikationsregel.|2=Tipp|3= Tipp}}|2=Tipp|3=Tipp}} | ||
{{Lösung versteckt|1= | {{Lösung versteckt|1= | ||
Version vom 28. November 2020, 13:49 Uhr
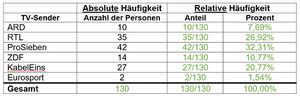
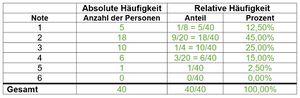
Absolute und relative Häufigkeit
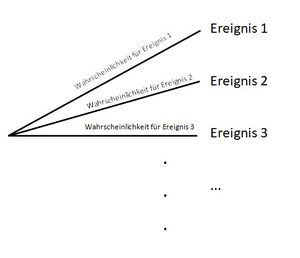
Zufallsexperimente
Laplace-Experimente