Benutzer:Lukas WWU-6/Testseite: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: „=== Spielwiese === ==== Schreiben im Wiki ==== Neben normalem Text kann man auch ''kursiven'' oder '''fett gedruckten''' Text schreiben. '''''Ebenso ist eine K…“) Markierung: Quelltext-Bearbeitung 2017 |
Keine Bearbeitungszusammenfassung Markierung: Quelltext-Bearbeitung 2017 |
||
| (8 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
=== Spielwiese === | ===Spielwiese=== | ||
==== Schreiben im Wiki ==== | |||
====Schreiben im Wiki==== | |||
Neben normalem Text kann man auch ''kursiven'' oder '''fett gedruckten''' Text schreiben. '''''Ebenso ist eine Kombination aus beidem möglich'''''. <span style="color:orange">Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.</span> | Neben normalem Text kann man auch ''kursiven'' oder '''fett gedruckten''' Text schreiben. '''''Ebenso ist eine Kombination aus beidem möglich'''''. <span style="color:orange">Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.</span> | ||
====Vorlagen==== | |||
{{Lösung versteckt|1=Ganz einfach per Mausklick aktivierbar|2=Versteckte Hinweise und Lösungen anzeigen|3=Hier könnte Ihre Werbung stehen.}} | |||
{{Box|Aufgabe|Inhalt|Arbeitsmethode}} | |||
{{Box|Übung|Inhalt|Üben}} | |||
{{Box|Merksatz|Inhalt|Merke}} | |||
====Dateien==== | |||
Basketballwurf GIF aus ZUM Projekte | |||
[[Datei:GIF Basketball.gif|zentriert|rahmenlos]] | |||
Griechische Landschildkröte aus Wikipedia | |||
[[File:WegehauptThbGriechenland1.jpg|zentriert|thumb|Testudo hermanni boettgeri in ihrer griechischen Heimat|alt=Testudo hermanni boettgeri in ihrer griechischen Heimat]] | |||
====Interaktive Applets==== | |||
Instrumente Zuordnen von LearningApps | |||
{{LearningApp|width:100%|height:500px|app=3828161}} | |||
===Kombinationen=== | |||
==Wiederholung: Eigenschaften von ganzrationalen Funktionen== | |||
In diesem Abschnitt werden wir kurz die Eigenschaften von ganzrationalen Funktionen wiederholen. Solltest du das Kapitel [[Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung]] noch nicht bearbeitet haben, empfehlen wir dir, dich zuerst damit vertraut zu machen. Wenn du dich fit fühlst beim Thema Funktionseigenschaften, kannst du die Wiederholung überspringen und dein Wissen im Quiz im unteren Bereich dieses Abschnitts testen. | |||
{{Box|1= Definition: Ganzrationale Funktionen | |||
|2= Eine '''Ganzrationale Funktion''' nennt man auch '''Polynomfunktion''' oder kurz '''Polynom'''. | |||
Beispiele sind: | |||
<math>f(x)=3x^4-2x^2+7</math> | |||
<math>f(x)=-10x^3-9x^2+x</math> | |||
Ganzrationale Funktionen sind Summen von Potenzfunktionen. Die Zahlen, mit denen einzelne Potenzfunktionen multipliziert werden, nennt man '''Koeffizienten'''. Den Wert des größten Exponenten nennt man den '''Grad der Funktion'''. | |||
Die Koeffizienten des ersten Beispiels sind <math>3</math>, <math>-2</math> und <math>7</math>. Der Grad ist <math>4</math>, sodass man sagt, es handelt sich um eine Funktion <math>4.</math> Grades. | |||
|3= Merksatz}} | |||
{{Box|1= Schnittpunkte | |||
|2= {{Lösung versteckt | |||
|1= Den Schnittpunkt einer Funktion mit der y-Achse nennt man '''<math>y</math>-Achsenabschnitt'''. Ist <math>y_s</math> der <math>y</math>-Achsenabschnitt einer Funktion <math>f</math>, liegt der Punkt <math>P_y(0|y_s)</math>, dessen x-Wert gleich <math>0</math> ist, auf dem Funktionsgraphen von <math>f</math>. | |||
Den <math>y</math>-Achsenabschnitt errechnest Du, indem Du in den Funktionsterm für <math>x</math> 0 einsetzt: <math>f(0)=y_s</math>. | |||
<ggb_applet id="vzq4hbez" width="800" height="400" /> | |||
{{Lösung versteckt | |||
|1= <math>f(x)=2x^3+3x+4</math> | |||
<math>\Rightarrow f(0)=2 \cdot 0^3+3 \cdot 0+4=4</math> | |||
<math>\Rightarrow P_y(0|4)</math> | |||
|2= Beispiel anzeigen | |||
|3= Beispiel verbergen}} | |||
Der <math>y</math>-Achsenabschnitt ist immer gleich dem letzten Koeffizienten der Funktion, welcher nicht mit <math>x</math> multipliziert wird. Sie lässt sich also immer aus der Funktionsgleichung ablesen. | |||
|2= Schnittpunkte mit der y-Achse | |||
|3= Schnittpunkte mit der y-Achse einklappen}} | |||
{{Lösung versteckt | |||
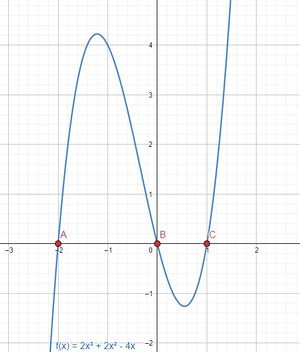
|1= Scheidet eine Funktion <math>f(x)</math> die '''x-Achse''', so liegt ein Punkt <math>P_x(x_s|0)</math>, dessen y-Wert gleich <math>0</math> ist, auf dem Funktionsgraphen. Man bezeichnet einen Schnittpunkt mit der x-Achse in der Regel als '''Nullstelle'''. | |||
Ganzrationale Funktionen können mehr als eine Nullstelle haben. Um genau zu sein, kann eine ganzrationale Funktion maximal so viele Nullstellen haben, wie der Wert ihres Grades beträgt. Ist ihr Grad außerdem ungerade, so haben sie mindestens eine Nullstelle. | |||
[[Datei:Beispiel Nullstellen.jpg|mini|zentriert]] | |||
Um die Nullstellen einer Funktion <math>f(x)</math> zu berechnen, setzt du den Funktionsterm <math>=0</math> und löst die Gleichung nach <math>x</math> auf. Verfahren zur Lösung, die Du kennen könntest, sind die pq-Formel, das Faktorisierungsverfahren, das Substitutuionsverfahren oder die Polynomdivision. | |||
{{Lösung versteckt | |||
|1= <math>f(x)=3x^2-9x-12=0</math> <math> \mid :3</math> | |||
<math> \Leftrightarrow x^2-3x-4=0</math> | |||
<math>p=-3</math> , <math>q=-4</math> | |||
<math>x_{1/2}=- \frac{p}{2} \pm \sqrt{( \frac{p}{2} )^2 -q}</math> | |||
<math>x_{1/2}=- \frac{-3}{2} \pm \sqrt{( \frac{-3}{2})^2-(-4)}</math> | |||
<math>x_{1/2}=1,5 \pm \sqrt{6,25}</math> | |||
<math>x_{1/2}=1,5 \pm 2,5</math> | |||
<math>x_1=4</math> , <math>x_2=-1</math> | |||
|2= Beispiel pq-Formel anzeigen | |||
|3= Beispiel pq-Formel verbergen}} | |||
{{Lösung versteckt | |||
|1= <math>f(x)=x^3-4x^2+4x=0</math> | |||
Der Faktor <math>x</math> kann ausgeklammert werden. | |||
<math>\Leftrightarrow x \cdot (x^2-4x+4)=0</math> | |||
<math>\Rightarrow x_1 = 0</math> ist die erste Nullstelle. Weitere Nullstellen ergeben sich, wenn der Ausdruck in den Klammern <math>=0</math> wird. | |||
<math> \Rightarrow x^2-4x+4=0</math> | |||
<math> \Rightarrow x_{2/3}=- \frac{-4}{2} \pm \sqrt{( \frac{-4}{2} )^2 -4}</math> | |||
<math> \Rightarrow x_2=2</math> | |||
Die Nullstellen sind <math>x_1=0</math> und <math>x_2=2</math> | |||
|2= Beispiel Faktorisierungsverfahren anzeigen | |||
|3= Beispiel Faktorisierungsverfahren verbergen}} | |||
|2= Schnittpunkte mit der x-Achse | |||
|3= Schnittpunkte mit der x-Achse einklappen}} | |||
|3= Beispiel}} | |||
{{Box|1= Monotonie | |||
|2= Das Monotonieverhalten einer Funktion beschreibt den Verlauf des Graphen einer Funktion. Die Montonie gibt an, ob eine Funktion fällt, steigt oder konstant ist. | |||
{{Lösung versteckt | |||
|1= {{LearningApp|width:100%|height:500px|app=p7pny09y220}} | |||
|2= Übung zur Monotonie | |||
|3= Übung zur Monotonie verbergen}} | |||
|3= Beispiel}} | |||
{{Box|1= Symmetrie | |||
|2= {{Lösung versteckt | |||
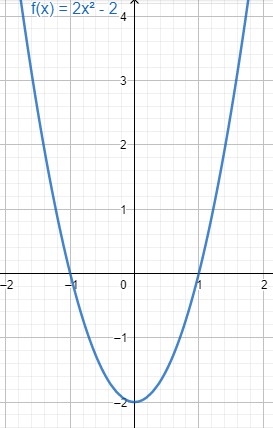
|1= Ist eine Funktion achsensymmetrisch, so spiegelt sich der Funktionsgraph an der y-Achse. Der Graph einer ganzrationalen Funktion ist genau dann achsensymmetrisch, wenn die Funktionsgleichung nur aus geraden Exponenten besteht. Außerdem gilt für achsensymmetrische Funktionen <math>f(-x)=f(x)</math>. | |||
[[Datei:Beispiel Achsensymmetrie.jpg|mini|zentriert]] | |||
|2= Achsensymmetrie | |||
|3= Achsensymmetrie verbergen}} | |||
{{Lösung versteckt | |||
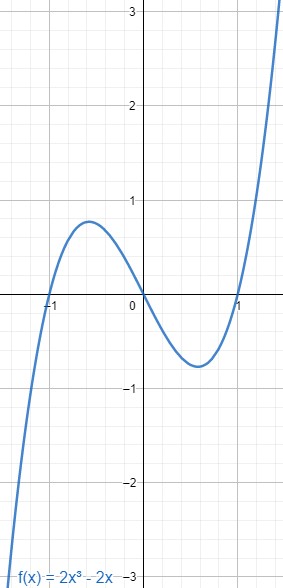
|1= Ist eine Funktion punktsymmetrisch, so wird eine Hälfte des Graphen am Koordinatenursprung auf die andere gespiegelt wird. Der Graph einer ganzrationalen Funktion ist genau dann punktsymmetrisch, wenn die Funktionsgleichung nur aus ungeraden Exponenten besteht. Außerdem gilt für punktsymmetrische Funktionen <math>f(-x)=-f(x)</math>. | |||
[[Datei:Beispiel Punktsymmetrie.jpg|mini|zentriert]] | |||
|2= Punktsymmetrie | |||
|3= Punktsymmetrie verbergen}} | |||
{{Lösung versteckt | |||
|1= {{LearningApp|width:100%|height:500px|app=pxrh34xin20}} | |||
|2= Übung zur Symmetrie | |||
|3= Übung einklappen}} | |||
|3= Beispiel}} | |||
{{Box|1= Extrema und Wendepunkte | |||
|2= {{Lösung versteckt | |||
|1= Mit einem '''Extremwert''' bezeichnet man ein lokales oder globales Maximum (Hochpunkt) oder Minimum (Tiefpunkt). Nimmt der Funktionswert <math>f(x)</math> an einer Stelle <math>x</math> den größten bzw. kleinsten Wert innerhalb eines Intervalles um <math>x</math> an, so spricht man von einem lokalen Maximum bzw. lokalem Minimum. Ist der Funktionswert bei <math>x</math> der größte bzw. kleinste Wert für den gesamten Definitionsbereich der Funktion, so nennt man ihn globales Maximum bzw. globales Minimum. | |||
Ist <math>f(x)</math> eine Extremstelle, so spricht man auch von einer Extremstelle der Funktion <math>f</math> bei <math>x</math>. | |||
[[Datei:Extrema example de.svg|zentriert]] | |||
Bei der Berechnung von Extremstellen einer Funktion <math>f(x)</math> macht man sich die Eigenschaften der Ableitung <math>f'(x)</math> zu Nutze: Eine Tangente, die an einer Extremstelle <math>x_1</math> angelegt wird, ist parallel zur <math>x</math>-Achse. Die Steigung ist also <math>0</math>. Die Ableitung <math>f'(x_1)</math> an dieser Stelle ist folglich <math>=0</math>. | |||
Für alle Extremstellen <math>x_n</math> gilt: | |||
<math>f'(x_n)=0</math> | |||
Das ist das '''Notwendige Kriterium'''. | |||
Will man nun prüfen, ob es sich um ein Maximum oder um ein Minimum handelt, zieht man die zweite Ableitung <math>f''(x)</math> hinzu. | |||
Das '''Hinreichende Kriterium''' lautet: | |||
*<math>f''(x)<0 \Rightarrow</math> Es liegt ein Maximum vor. | |||
*<math>f''(x)>0 \Rightarrow</math> Es liegt ein Minimum vor. | |||
*<math>f''(x)=0 \Rightarrow</math> Es liegt eine Sattelstelle vor. | |||
|2= Extremstellen | |||
|3= Extremstellen verbergen}} | |||
{{Lösung versteckt | |||
|1= {{LearningApp|width:100%|height:500px|app=pxcek6u8t20}} | |||
|2= Übung Extremstellen | |||
|3= Übung Extremstellen verbergen}} | |||
{{Lösung versteckt | |||
|1= Mit einem '''Wendepunkt''' bezeichnet meine eine Stelle des Funktionsgraphen, an der sich das Krümmungsverhalten des Graphen ändert. Das kann ein Wechsel von einer Rechts- zu einer Linkskurve oder von einer Links- zu einer Rechtskurve sein. | |||
[[File:Animated illustration of inflection point.gif|zentriert|thumb|Krümmungsverhalten der Funktion sin(2x). Die Tangente ist blau gefärbt in konvexen Bereichen (Linkskurve), grün gefärbt in konkaven Bereichen (Rechtskurve) und rot gefärbt bei Wendepunkten.]] | |||
An einem Wendepunkt ist die Steigung der Funktion innerhalb einer Umgebung um den Wendepunkt maximal. Das erkennst Du gut auf der Grafik oben. | |||
Ist die Steigung an einer Stelle <math>x_W</math> maximal, so ist bei der Ableitung an dieser Stelle <math>f'(x_W)</math> ein Extremum. Um die Wendestellen einer Funktion <math>f</math> zu finden, musst du die Ableitung <math>f'</math> also nach Extremstellen untersuchen. | |||
|2= Wendepunkte | |||
|3= Wendepunkte verbergen}} | |||
{{Lösung versteckt | |||
|1= {{LearningApp|width:100%|height:500px|app=po7ph1zgc20}} | |||
|2= Übung Wendepunkte | |||
|3= Übung Wendepunkte verbergen}} | |||
|3= Beispiel}} | |||
{{Box|1= Funktionsgleichung aufstellen | |||
|2= {{Lösung versteckt | |||
|1= Bei dem Aufstellen einer Funktionsgleichung für eine ganzrationale Funktion geht es darum, die Werte aller Koeffizienten herauszufinden. Das Vorgehen ist vergleichbar mit einem Puzzle: Verschiedene Informationen über die Funktion sind Dir bekannt, die Schwierigkeit besteht nun darin, diese Informationen zu sortieren. | |||
Der erste Schritt ist immer, beim Rahmen anzufangen. Welche Form wird der Funktionsterm haben? Handelt es sich beispielsweise um eine Funktion 2. Grades, so hat der Term die Form <math>f(x)=ax^2+bx+c</math> mit den drei unbekannten Koeffizienten <math>a</math>, <math>b</math> und <math>c</math>. Eine Funktion 3. Grades hätte die Form <math>f(x)=ax^3+bx^2+cx+d</math>. Und so weiter. | |||
Als nächstes können Dir Informationen über die Symmetrie helfen. Falls die Funktion achsensymmetrisch ist, weißt Du, dass alle Koeffizienten vor ungeraden Exponenten gleich <math>0</math> sind. Im Fall von Punktsymmetrie sind alle Koeffizienten vor geraden Exponenten gleich <math>0</math>. | |||
Dein nächstes Ziel ist es verschiedene Gleichungen, die die unbekannten Koeffizienten enthalten aufzustellen. Wie Du ein solches System aus Gleichungen dann auflöst zeigen wir Dir unten. | |||
Um aber zuerst Gleichungen zu erhalten, setzt du <math>x</math>- und <math>y</math>-Koordinaten von bekannten Punkten des Graphen in Deinen Rahmen ein. Wenn Du spezielle Informationen über Extremstellen, Wendepunkte oder die Ableitung allgemein hast, musst Du diese Koordinaten in den Rahmen der Ableitung der Funktion einsetzen. Diesen berechnest Du aus den bekannten Ableitungsregeln: | |||
Sei die gesuchte Funktion vom 3. Grad. | |||
Rahmen: <math>f(x)=ax^3+bx^2+cx+d</math> | |||
1. Ableitung des Rahmens: <math>f(x)=3ax^2+2bx+c</math> | |||
2. Ableitung des Rahmens: <math>f(x)=6ax+2b</math> | |||
|2= Funktionsgleichung aufstellen | |||
|3= Funktionsgleichung aufstellen verbergen}} | |||
|3= Beispiel}} | |||
{{Box|1= Funktionsgraphen zeichnen | |||
|2= {{Lösung versteckt | |||
|1= Um den Funktionsgraphen zu zeichnen benötigst Du möglichst viele Informationen über den Graphen. | |||
Besonders hilfreiche Informationen sind Achsenschnittpunkte sowie Nullstellen, Extremstellen und Wendestellen. Kennst du den Funktionsterm kannst Du mit einer Wertetabelle darüber hinaus weitere Punkte errechnen, die auf dem Graphen liegen müssen. | |||
|2= Funktionsgraphen zeichnen | |||
|3= Funktionsgraphen zeichnen einklappen}} | |||
|3= Beispiel}} | |||
===Quiz=== | |||
{{Box|1= Quiz zu den Eigenschaften ganzrationaler Funktionen <span style="color: yellow"></span> | |||
|2={{Lösung versteckt | |||
|1= Kreuze die richtigen Antworten an. Es kann mehr als eine Antwort pro Frage richtig sein. Drück am Ende auf "Speichern" um Deine Lösungen zu überprüfen. | |||
<quiz display="simple"> | |||
{ Welche der folgenden Aussagen ist wahr? } | |||
+ 1 Eine Funktion hat an einem Hochpunkt dieselbe Steigung, wie an einem Tiefpunkt. | |||
- 2 Ein Polynom 3. Grades ist immer punktsymmetrisch. | |||
+ 3 Ein Polynom 3. Grades ist nie achsensymmetrsich. | |||
+ 4 Das Hinreichende Kriterium für Extremstellen unterscheidet Hochpunkte, Tiefpunkte und Sattelstellen. | |||
- 5 Direkt hinter einem Hochpunkt ist die Steigung einer Funktion positiv. | |||
+ 6 Die zweite Ableitung eines Polynoms 2. Grades ist konstant. | |||
+ 7 Eine parabelförmige Funktion hat zwei oder weniger Nullstellen. | |||
- 8 <math>f(x)=5x^2+10x</math> geht nicht durch den Ursprung <math>(0|0)</math>. | |||
- 9 Zwischen zwei Tiefpunkten liegt genau ein Wendepunkt. | |||
+ 10 An einem Wendepunkt von <math>f</math> hat die Ableitung <math>f'</math> ein Extremum oder dieser Wendepunkt ist ein Sattelpunkt. | |||
{ <math>f'(x)</math> ist nur auf dem Intervall <math>[1,3]</math> positiv. } | |||
- 1 <math>f(x)</math> steigt im Bereich <math>[3,\infty[</math>. | |||
+ 2 <math>f(x)</math> hat mindestens zwei Extremstellen. | |||
- 3 <math>f'(x)</math> hat mindestens Grad 3. | |||
+ 4 Im Intervall <math>[1,3]</math> hat <math>f(x)</math> einen Wendepunkt. | |||
{ <math>f(x)=x^3+2x^2+3x+4</math> } | |||
+ 1 <math>f''(x)</math> ist streng monoton steigend. | |||
+ 2 <math>f'(x)</math> schneidet die <math>y</math>-Achse im Punkt <math>P(0|3)</math>. | |||
- 3 <math>f(x)</math> ist eine Funktion 4. Grades. | |||
- 4 <math>f'(x)</math> ist punktsymmetrisch. | |||
{ <math>f(x)=3x^4+2x^2-10</math> } | |||
+ 1 <math>f''(x)</math> hat den Grad 2. | |||
- 2 <math>f(x)</math> ist punktsymmetrisch. | |||
- 3 <math>f(x)</math> scheidet die <math>y</math>-Achse beim Wert 10. | |||
+ 4 <math>f'(x)</math> ist punktsymmetrisch. | |||
{ <math>f(x)</math> hat einen Hochpunkt an der Stelle <math>x_1</math> } | |||
- 1 <math>f''(x_1)=0</math> | |||
- 2 <math>f''(x_1)>0</math> | |||
- 3 <math> f'(x_1)<0</math> | |||
+ 4 <math> f''(x_1)<0</math> | |||
{ <math>f(x)= \frac{1}{2}x^2+x-3</math> und <math>g(x)= 3x^2+ \frac{1}{3}x+7</math> } | |||
- 1 <math>f(x)+g(x)= \frac{3}{2}x^2+\frac{1}{3}x-21</math>. | |||
+ 2 <math>f(x)-g(x)=- \frac{5}{2}x^2+ \frac{2}{3}x-10</math> | |||
+ 3 <math>f(x)+g(x)= \frac{7}{2}x^2+ \frac{4}{3}x+4</math> | |||
- 4 <math>g(x)</math> hat einen höheren Grad als <math>f(x)</math>. | |||
</quiz> | |||
|2= Quiz | |||
|3= Quiz verbergen}} | |||
|Farbe =#fce903|3= Aufgabe}} | |||
==Einführung: lineare Gleichungen== | |||
Auf dieser Seite lernst Du, wie Du '''Gleichungssysteme mit mehr als einer Variablen lösen''' kannst. Falls Du dir noch unsicher bist, wie man eine Gleichung mit nur einer Variable löst, versuche folgendes ''Beispiel ''zu lösen. Falls Du das aber noch kannst, dann überspringe das Beispiel gerne.{{Box|Beispiel|Löse folgende Gleichung: | |||
<math>6x-5=37</math> | |||
{{Lösung versteckt|1= Bringe zuerst die Variable alleine auf eine Seite und Teile dann durch die Anzahl der Variable.|2=Hinweis zum Vorgehen|3=Alles klar, weiter geht's!}} | |||
{{Lösung versteckt|1=<math>x=7</math> |2=Lösung|3=Lösung ausblenden}}|Beispiel | |||
}} | |||
Aktuelle Version vom 22. Mai 2020, 13:19 Uhr
Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Dateien
Basketballwurf GIF aus ZUM Projekte
Griechische Landschildkröte aus Wikipedia
Interaktive Applets
Instrumente Zuordnen von LearningApps
Kombinationen
Wiederholung: Eigenschaften von ganzrationalen Funktionen
In diesem Abschnitt werden wir kurz die Eigenschaften von ganzrationalen Funktionen wiederholen. Solltest du das Kapitel Digitale Werkzeuge in der Schule/Basiswissen Analysis/Eigenschaften von Funktionen und Funktionsuntersuchung noch nicht bearbeitet haben, empfehlen wir dir, dich zuerst damit vertraut zu machen. Wenn du dich fit fühlst beim Thema Funktionseigenschaften, kannst du die Wiederholung überspringen und dein Wissen im Quiz im unteren Bereich dieses Abschnitts testen.
Quiz
Einführung: lineare Gleichungen
Auf dieser Seite lernst Du, wie Du Gleichungssysteme mit mehr als einer Variablen lösen kannst. Falls Du dir noch unsicher bist, wie man eine Gleichung mit nur einer Variable löst, versuche folgendes Beispiel zu lösen. Falls Du das aber noch kannst, dann überspringe das Beispiel gerne.