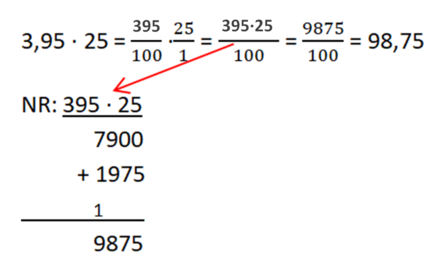Herta-Lebenstein-Realschule/Lernpfad Rechnen mit Dezimalbrüchen/2) Dezimalbrüche multiplizieren

2) Dezimalbrüche multiplizieren

Eine weitere Frage, die wir zu Beginn an die Weitsprungergebnisse beim Sportabzeichentag gestellt haben, war folgende:

Wenn du den besten Sprung betrachtest, wie weit kämst du dann mit 25 Sprüngen für die gesamte Klasse?

Nehmen wir noch einmal die Ergebnisse von Tom: 3m; 3,2m und 3,95m.

Die Rechnung heißt hier also: 3,95 m · 25

Um dies beantworten zu können, müssen wir Dezimalbrüche multiplizieren können. Dies lernst du auf dieser Seite.

Beginnen wir mit einer leichteren Frage:

Multiplizieren mit 10, 100, 1000

Wie weit käme man bei 10 Sprüngen? Wie weit käme man mit 100 Sprüngen usw.?

Das kannst du sicher im Kopf berechnen. Fällt dir etwas auf?

2.1 Dezialbrüche mit 10, 100, 1000 multiplizieren

Dezimalbrüche mit 10, 100, 1000 multiplizieren

Beim Multiplizieren mit 10, 100, 1000 (diese Zahlen heißen auch Zehnerpotenzen) wird das Komma nach rechts verschoben. Es wird um so viele Stellen verschoben, wie die Zehnerpotenz Nullen hat.

Schau das Erklärvideo on:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 1: Multiplizieren mit Zehnerpotenzen

Bearbeite die folgende App und danach S. 124 Nr. 3 im Heft.

2.2 Dezimalbrüche multiplizieren

Wie können wir nun die Frage beantworten, wie weit die gesamte Klasse mit dem besten Sprung von Tom gesprungen wäre?

Wir müssen 3,95m · 25 rechnen.

Idee 1: Wandle 3,95 m in eine kleinere Einheit um, berechne und wandle zurück in m um.

Idee 2: Wir können Brüche multiplizieren, dies übertragen wir nun:

Wir multiplizieren also die Zahlen in der Nebenrechnung ohne Komma, der Nenner 100 gibt dann an, dass das Ergebnis zwei Nachkommastellen haben muss.

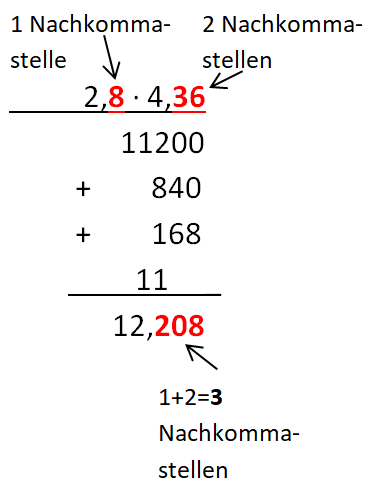
Geht das auch mit zwei Dezimalbrüchen?

Merke: Multiplizieren von Dezimalbrüchen

Beim Multiplizieren von Dezimalbrüchen rechnen wir schriftlich (ohne das Komma zu beachten).

Dann setzen wir das Komma im Ergebnis so, dass das Ergebnis genau so viele Nachkommastellen hat, wie beide Faktoren zusammen.

Das Video fasst die Regel noch einmal zusammen:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 2

Löse die folgenden Apps. Wie viele Kommastellen hat das Ergebnis?

Übung 3

Bearbeite nun S. 129 Nr. 5 , 6 und 11 schriftlich im Heft

Lösungswort: KROATIEN

Beispiel für den Überschlag: a) 30 · 7 = 210;b) 0,03 · 12 = 0,36; d) 170 · 0,1 = 17; e) 80· 0,05 = 4; f) 0,7 · 800 = 560

Lösungen zum Vergleichen (Du musst ausführliche Rechnungen im Heft notiert haben!) a) a) 195,02 b) 0,342 c) 1505,856 d) 14,9468 e) 3,5196 f) 574,585

Wo finden wir weitere Beispiele zur Multiplikation von Dezimalbrüchen im Sport?

Wir gehen schwimmen. Das Becken ist 28,5 m lang und 21,6 m breit. Welche Fläche hat der Beckenboden?

Übung 4

Berechne S. 130 Nr. 16, 17 und 22. Denke an eine übersichtliche Darstellung. geg:… ges:… R:…

Antwort:…

Flächeninhalt eines Rechtecks A = a · b. Multipliziere schriftlich, denke an das Komma im Ergebnis

Ergänze die linke Figur zu einer großen Fläche und subtrahiere dann das zu viel berechnete Rechteck

Berechne zunächst das Volumen des Beckens (des Quaders) mit V = a · b · c , wobei c hier die Wassertiefe ist.

Berechne zunächst das Volumen des abgeflossenen Wassers mit V = a · b · c , wobei c hier die Höhe ist, um die der Wasserspiegel gesunken ist.

Berechne die Fläche, die gefliest werden muss. Dies ist die Oberfläche eines Quaders, aber ohne die obere Fläche (die Deckfläche fehlt).

zurück zur Startseite

3) Dezimalbrüche dividieren