Herta-Lebenstein-Realschule/Rechnen mit Brüchen/Verbindung der Rechenarten

zurück zur Seite der Herta-Lebenstein-Realschule

0) Vorwissen

1) Addieren und subtrahieren von Brüchen
2) Multiplizieren von Brüchen
3) Dividieren von Brüchen
4) Verbindung der Rechenarten

5) Bruchteile beliebiger Größen

Verbindung der Rechenarten

Bist du fit beim Rechnen mit Brüchen?

Bevor du die Rechenarten gemischt anwendest, wiederhole die Rechenregeln zum Rechnen mit Brüchen zu den Grundrechenarten auf der Seite Aufgabenfuchs.

• Grundrechenarten Brüche Aufgabenfuchs

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

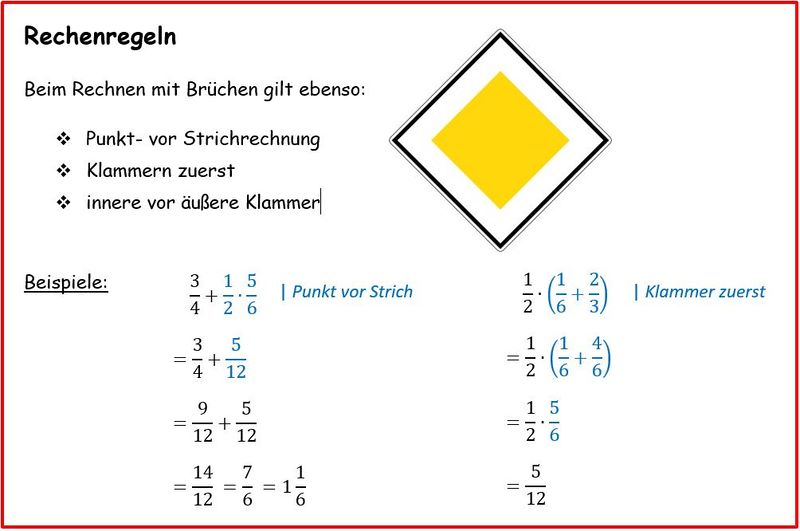
Hefteintrag: Rechenregeln (Vorrangregeln)

Übung 1 - Was muss zuerst gerechnet werden?

Markiere im nachfolgenden GeoGebra-Applet des FLINK-Teams die Rechnung, die zuerst gerechnet werden muss.

Originallink https://www.geogebra.org/m/phkmedu6

Übung 2

Löse auf der Seite realmath so viele Aufgaben, bis du jeweils mindestens 300 Punkte gesammelt hast.

• Übung 1
• Übung 2
• Rechenbaum Level 1
• Rechenbaum Level 2
• Rechenbaum Level 3
• Rechenbaum Level 4
• Rechenbaum Champion
• Rechenbaum Top Profi

Übung 3

Schreibe die Aufgabe in dein Heft und löse sie. Beachte die Vorrangregeln. Rechne ausführlich, so wie im Merkkasten beschrieben.
a) $\tfrac{5}{8} · \tfrac{4}{5} - \tfrac{1}{3}$
b) $\tfrac{4}{5} : \tfrac{2}{3} - \tfrac{1}{5}$
c) $\tfrac{5}{6} + \tfrac{2}{3} · \tfrac{1}{2}$
d) $\tfrac{3}{4} - \tfrac{1}{6} : \tfrac{1}{3}$
e) $\tfrac{1}{7} + \tfrac{5}{7}$ : 5
f) $\tfrac{2}{3} · (\tfrac{1}{8} + \tfrac{3}{4}$)
g) ($\tfrac{4}{5} + \tfrac{1}{15}) : (\tfrac{1}{5} + \tfrac{1}{2})$
h) $\tfrac{3}{4} \cdot (\tfrac{2}{5} - \tfrac{1}{3})$
i) $\tfrac{5}{6} + \tfrac{1}{2} \cdot \tfrac{2}{3}$

j) $(\tfrac{2}{3} + \tfrac{1}{4}) \cdot \tfrac{3}{5}$

Vergleiche deine Lösungen:

a) $\tfrac{5}{8} \cdot \tfrac{4}{5} - \tfrac{1}{3}$
  = $\tfrac{5·4}{8·5} - \tfrac{1}{3}$ KÜRZEN
  = $\tfrac{1·1}{2·1} - \tfrac{1}{3}$
  = $\tfrac{1}{2} - \tfrac{1}{3}$
  = $\tfrac{3}{6} - \tfrac{2}{6}$
  = $\tfrac{1}{6}$

b) $\tfrac{4}{5} : \tfrac{2}{3} - \tfrac{1}{5}$
  = $\tfrac{4}{5} \cdot \tfrac{3}{2} - \tfrac{1}{5}$
  = $\tfrac{4·3}{5·2} - \tfrac{1}{5}$ KÜRZEN
  = $\tfrac{2·3}{5·1} - \tfrac{1}{5}$
  = $\tfrac{6}{5} - \tfrac{1}{5}$
  = $\tfrac{5}{5}$
  = 1

c) $\tfrac{5}{6} + \tfrac{2}{3} \cdot \tfrac{1}{2}$
  = $\tfrac{5}{6} + \tfrac{2·1}{3·2}$ KÜRZEN
  = $\tfrac{5}{6} + \tfrac{1·1}{3·1}$
  = $\tfrac{5}{6} + \tfrac{1}{3}$
  = $\tfrac{5}{6} + \tfrac{2}{6}$
  = $\tfrac{7}{6}$
  = 1$\tfrac{1}{6}$

d) $\tfrac{3}{4} - \tfrac{1}{6} : \tfrac{1}{3}$
  = $\tfrac{3}{4} - \frac{1}{6} · \tfrac{3}{1}$
  = $\tfrac{3}{4} - \tfrac{1·3}{6·1}$ KÜRZEN
  = $\tfrac{3}{4} - \tfrac{1·1}{2·1}$
  = $\tfrac{3}{4} - \tfrac{1}{2}$
  = $\tfrac{3}{4} - \tfrac{2}{4}$
  = $\tfrac{1}{4}$

e) $\tfrac{1}{7} + \tfrac{5}{7} : 5$
  = $\tfrac{1}{7} + \tfrac{5}{7·5}$ KÜRZEN
  = $\tfrac{1}{7} + \tfrac{1}{7·1}$
  = $\tfrac{1}{7}+ \tfrac{1}{7}$
  = $\tfrac{2}{7}$

   
f) $\tfrac{2}{3} \cdot (\tfrac{1}{8} + \tfrac{3}{4})$
  = $\tfrac{2}{3} \cdot (\tfrac{1}{8} + \tfrac{6}{8})$
  = $\tfrac{2}{3} \cdot \tfrac{7}{8}$
  = $\tfrac{2·7}{3·8}$ KÜRZEN
  = $\tfrac{1·7}{3·4}$
  = $\tfrac{7}{12}$
  
g) $(\tfrac{4}{5} + \tfrac{1}{15}) \div (\tfrac{1}{5} + \frac{1}{2})$
  = $(\tfrac{13}{15} + \tfrac{1}{15}$) : $(\tfrac{2}{10} + \tfrac{5}{10})$
  = $\tfrac{14}{15} : \tfrac{10}{7}$
  = $\tfrac{14}{15} · \tfrac{7}{10}$
  = $\tfrac{14·7}{15·10}$ KÜRZEN
  = $\tfrac{7·7}{15·5}$
  = $\tfrac{49}{75}$

h) $\tfrac{3}{4} \cdot (\tfrac{2}{5} - \tfrac{1}{3})$
  = $\tfrac{3}{4} \cdot (\tfrac{6}{15} - \tfrac{5}{15})$
  = $\tfrac{3}{4} \cdot \tfrac{1}{15}$
  = $\tfrac{3·1}{4·15}$ KÜRZEN
  = $\tfrac{1·1}{4·5}$
  = $\tfrac{1}{20}$

i) $\tfrac{5}{6} + \tfrac{1}{2} \cdot \tfrac{2}{3}$
  = $\tfrac{5}{6} + \tfrac{1·2}{2·3}$ KÜRZEN
  = $\tfrac{5}{6} + \tfrac{1·1}{1·3}$
  = $\tfrac{5}{6} + \tfrac{1}{3}$
  = $\tfrac{15}{18} + \tfrac{6}{18}$
  = $\tfrac{21}{18}$
  = $\tfrac{7}{6}$
  = 1$\tfrac{1}{6}$

j) $(\tfrac{2}{3} + \tfrac{1}{4}) \cdot \tfrac{3}{5}$
  = $(\tfrac{8}{12} + \tfrac{3}{12}) \cdot \tfrac{3}{5}$
  = $\tfrac{11}{12} \cdot \tfrac{3}{5}$ 
  = $\tfrac{11·3}{12·5}$ KÜRZEN
  = $\tfrac{11·1}{4·5}$ 

= $\tfrac{11}{20}$

Übung 4

Löse die nachfolgenden LearningApps

5) Bruchteile beliebiger Größen