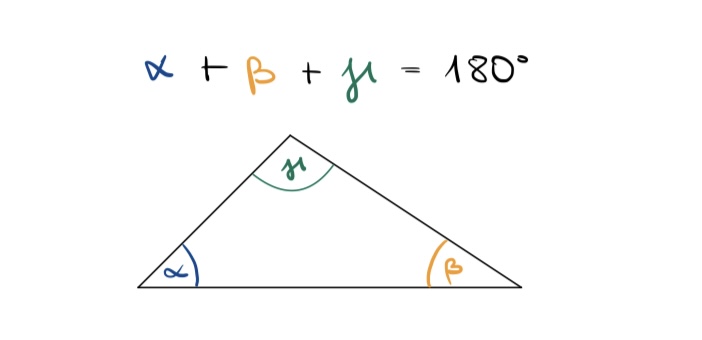Geometrie im Dreieck/Geheimcode der Geometrie

Informationskästchen

Info

In diesem Lernpfadkapitel tauchen wir in die spannende Welt der Dreiecke ein und erforschen die Geheimnisse der Innenwinkelsumme. Bei den Aufgaben unterscheiden wir folgende Typen:

• In Aufgaben, die orange gefärbt sind, kannst du grundlegende Kompetenzen wiederholen und vertiefen.
• Aufgaben in pinker Farbe sind Aufgaben mittlerer Schwierigkeit.
• Und Aufgaben mit lilanem Streifen sind Knobelaufgaben.

Viel Erfolg!

Einführung

Was ist die Innenwinkelsumme in einem Dreieck?

Die Summe der Innenwinkel in einem Dreieck beträgt immer 180 Grad. Dies wird durch den Innenwinkelsatz beschrieben.

Innenwinkelsumme leicht erklärt - klicke hier, wenn du noch unsicher bist! https://studyflix.de/mathematik/winkelsumme-5503

Stimmt das auch wirklich? Wenn ja, dann müssten die drei Innenwinkel im Dreieck einen gestreckten Winkel ergeben. Das sollte dann also in etwa so aussehen:

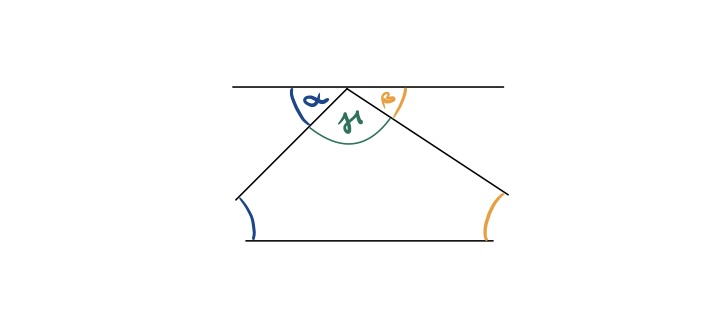
Reiße die zwei Winkel α und β deines Dreiecks (auf dem Arbeitsblatt) ab und prüfe, ob man sie an der Spitze zu einem gestreckten Winkel mit 180° anordnen kann.

Aufgabe 1

{{Box|Level 1|Erstere Hinweise sammeln

Datei:Level 1gelb.png

Euer erster Hinweis führt euch zu einem Dreieck, bei dem zwei Winkel gegeben sind: 50° und 60°. Der dritte Winkel ist jedoch verdeckt. Findet den verborgenen Winkel und zeigt rechnerisch, dass die Summe der Innenwinkel 180° beträgt. Erklärt warum dies immer so sein muss.

Level 2: Weitere Spuren entdecken

Euer nächster Hinweis befindet sich in einem gleichschenkligen Dreieck. Ihr wisst, dass die beiden Basiswinkel jeweils 65° betragen, aber der Winkel an der Spitze ist unleserlich. Berechnet diesen Winkel und erklärt rechnerisch, warum die Innenwinkelsumme 180° ergibt. Argumentiert, warum die Summe der Winkel im Dreieck immer diese Zahl ergibt, egal wie das Dreieck aussieht.

Level 3: Das letzte Rätsel

Auf dem letzten Teil eurer Jagd entdeckt ihr eine mysteriöse geometrische Nachricht: "In jedem Dreieck steht ein gestreckter Winkel, wenn man die Innenwinkel nebeneinanderlegt." Ihr sollt dies überprüfen, in dem ihr ein eigenes Dreieck konstruiert und die drei Innenwinkel nebeneinander anordnet. Zeigt, dass diese Winkel zusammen einen gestreckten Winkel (180°) ergeben und begründet rechnerisch und logisch, warum dies immer so ist.

Zusatzfrage: Überlegt, ob diese Regel auch für Vierecke gilt und begründet eure Antwort.

Aufgabe 2

Aufgabe 2.1

Berechne den fehlenden Winkel mithilfe des Innenwinkelsatzes!

Berechne den fehlenden Winkel γ, indem du die Winkel α und β von 180° abziehst.

Aufgabe 2.2

Erkenne die Innenwinkel des Dreiecks und berechne sie!

α und α' bilden einen rechten Winkel. Es gilt also α+α'=90°. Wie kannst du herausfinden, wie groß α ist?

γ und γ' sind Nebenwinkel. Es gilt also γ+γ'=180°. Wie kannst du herausfinden, wie groß γ' ist?

Berechne den fehlenden Winkel β mithilfe des Innenwinkelsatzes!

Aufgabe 2.3

Bestimme die Innenwinkel des Dreiecks!

α und α' sind Stufenwinkel. Wie groß ist dann α'?

β und β' sind Scheitelwinkel. Wie groß ist dann β?

Berechne den fehlenden Winkel γ mithilfe des Innenwinkelsatzes!

Aufgabe 4 (Sicherung)

Hier kommst du zurück zur Startseite des Kapitels: Geometrie im Dreieck