|
|
| Zeile 282: |
Zeile 282: |
| |Arbeitsmethode}} | | |Arbeitsmethode}} |
|
| |
|
| {{Box|[[Datei:MerksatzFlächen.jpg|mini]]Wie wachsen Flächeninhalte beim Skalieren|Beim Skalieren mit dem Faktor k wachsen (oder schrumpfen) Flächeninhalte mit dem Faktor k²|Merksatz}} | | {{Box|]Wachstum von Flächeninhalten beim Skalieren|[[Datei:MerksatzFlächen.jpg|200px|left]Beim Skalieren mit dem Faktor k wachsen (oder schrumpfen) Flächeninhalte mit dem Faktor k²|Merksatz}} |
|
| |
|
| {{Box|Idee|Mit Hilfe des Skalierungsfaktors kannst du die Flächeninhalte beliebiger vergrößerter oder verkleinerter Figuren sehr schnell berechnen|Unterrichtsidee }} | | {{Box|Idee|Mit Hilfe des Skalierungsfaktors kannst du die Flächeninhalte beliebiger vergrößerter oder verkleinerter Figuren sehr schnell berechnen|Unterrichtsidee }} |
Version vom 11. Mai 2022, 14:15 Uhr
Datei:Teetasse
In vielen Filmen spielen besonders große oder kleine Helden oder Heldinnen eine wichtige Rolle. Bekannte Beispiele sind der Waldhüter und Halbriese Hagrid der Harry-Potter-Filme oder die Titelfigur Alice aus Alice im Wunderland, die im Laufe der Handlung auf ein Zehntel ihrer Größe schrumpft. Zur Darstellung der Größenverhältnisse wird oft mit großem Aufwand die Kulisse in einer kleineren oder größeren Version nachgebaut. Doch worauf muss man achten, damit der Nachbau der Kulisse gelingt?
1. korrektes Vergrößern und Verkleinern. Worauf kommt es an?
Fehlersuche
Nur eines der drei kleinen Bilder zeigt eine korrekte Kopie des verzauberten Autos, mit dem Harry und Ron nach Hogwarts fliegen, nachdem sie den Zug verpasst haben.
Begründe deine Entscheidung!
Auf den anderen Bildern sind die Verhältnisse der Seitenlängen und Flächen nicht korrekt. Beispielsweise ist auf dem ersten Bild die Kühlerhaube zu lang, auf dem dritten zu kurz.
Frage
Worauf muss man achten, damit die Formen nicht verzerrren? Beantworte diese Frage mit Hilfe der Aufgabe "Harry-Logo"
Harrys Freundin Luna hat ein "Harry-Logo" entworfen. Durch geeignete Zauber kann sie es vergrößern und verkleinern, so dass sie es als Anstecknadel oder auch als Banner verwenden kann.
Überlege zunächst, wie du vorgehen würdest, um das Logo auf die doppelte Größe zu vergrößern bzw. halbe Größe zu verkleinern. Notiere stichpunktartig, wie sich
- Seitenlängen
- Winkeln
- Flächen
- Seitenverhältnissen
- Flächenverhältnissen (z.B. Buchstabe - Umrandung)
verändern.
Überprüfe deine Angaben anschließend mit Hilfe dem Applet "Logo".
Du kannst den Vergrößerungsfaktor - auch Skalierungsfaktor genannt - mit dem Schiebregler verändern.
Kreuze nun die richtigen Aussagen im Quiz an.
Fülle jetzt den Lückentext aus. Kontrolliere deine Lösung und übertrage sie auf dein Merkblatt|
Merke: Skalieren = Maßstäbliches Vergrößern oder Verkleinern von Figuren
Wenn die Formen nicht verzerren sollen, muss man eine Figur maßstäblich vergrößern oder verkleinern. Dabei werden alle Seitenlängen der Figur mit demselben positiven Faktor multipliziert. Dieser Faktor heißt auch Skalierungsfaktor, das maßstäbliche Vergrößern oder Verkleinern heißt auch skalieren. Ist der Skalierungsfaktor k größer als 1, so wird das Original vergrößert, ist k kleiner 1, wird das Original verkleinert. Beim Skalieren bleiben alle Winkel sowie die Seiten- und Flächenverhältnisse gleich. Figuren, die durch Skalierung auseinander entstehen, nennt man mathematisch ähnlich. zueinander.
Wie groß ist die Teetasse?
Nachdem Alice einen Zaubertrank getrunken hat, schrumpft sie auf ein Zehntel ihrer Größe.
- Gib den Skalierungfaktor an, mit dem die Teetasse vergrößert werden musste.
- Die originale Teetasse ist ca. 8 cm hoch und hat am oberen Rand einen Umfang von 28 cm. Berechne Höhe und Umfang der vergrößerten Teetasse.
- Sprinteraufgabe: Schätze die ungefähre Größe von Alice.
- Der Skalierungsfaktor beträgt 10.
- Die vergrößerte Teetasse ist 80 cm hoch und hat am oberen Rand einen Umfang von 280 cm = 2,80 m.
- Die Teetasse ist etwa zwei Drittel so groß wie Alice, die Schauspielerin müsste also ca. 1,20 m groß sein.
2. Wie wachsen Flächeninhalte beim Skalieren von Figuren?
Wie geht es weiter?
Du hast wahrscheinlich bereits festgestellt, dass Flächeninhalte beim Skalieren schneller wachsen (oder schrumpfen) als die Seitenlängen. Auch hier gibt es eine Gesetzmäßigkeit, die du herausfinden sollst. Schaue dir dazu zuerst einfache geometrische Formen an.
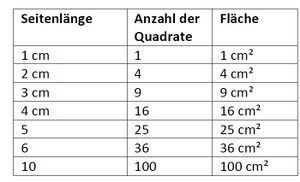
Quadratwachstum 1
Im Applet "Quadrate 1" siehst du zwei Quadrate mit der Seitenlänge 1 cm, also einem Flächeninhalt von 1 cm².
a) Betrachte zunächst vergrößerte Quadrate - das heißt, dass das Quadrat mit einem Faktor k > 1 skaliert wird:
- Vergrößere das rechte Quadrat nacheinander mit dem Faktor 2, 3 und 4, indem du den Skalierungsfaktor passend einstellst. Prüfe, wie oft das ursprüngliche Quadrat jeweils in das vergrößerte Quadrat passt. Du kannst dazu beliebig viele Kopien des Originalquadrats erzeugen und die Fläche des vergrößerten Quadrats damit auslegen. Trage die Anzahl der Quadrate in die Tabelle ein, die du auf dem Arbeitsblatt findest.
- Überlege, wie viele Quadrate du benötigen würdest, wenn der Vergrößerungsfaktor 5, 6 bzw. 10 betragen würde. Trage die Anzahl in der Tabelle ein.
- Gib an, welcher Zusammenhang zwischen Vergrößerungsfaktor k und Zahl der Quadrate besteht.
- Berechne den Flächeninhalt der vergrößerten Quadrate mit Hilfe der Anzahl der Quadrate. Trage den Flächeninhalt ebenfalls in die Tabelle ein.
- Gib eine Formel an, mit der sich der Flächeninhalt direkt mit Hilfe des Skalierungsfaktors k berechnen lässt. Trage sie auf dem Arbeitsblatt ein.
Kontrolliere deine Lösung!
- Wird das Quadrat mit dem Faktor k vergrößert, ist die Zahl der Quadrate k²
- Man muss den ursprünglichen Flächeninhalt lediglich mit der Anzahl der Quadrate multiplizieren, um den neuen Flächeninhalt zu erhalten.
- Wird ein Quadrat mit der Seitenlänge 1 cm mit dem Faktor k skaliert, so beträgt der Flächeninhalt k². Die Formel für den neuen Flächeninhalt Aneu=k².
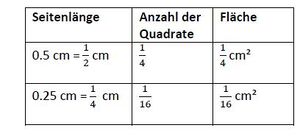
b) Jetzt sollst du Quadrat verkleinern, also mit einem Faktor k<1 skaliert werden:
- Setze die Konstruktion zurück (Symbol) und verkleinere das Quadrat nun mit den Faktoren 0,5 (gleich 1/4) und 0,25 (gleich 1/8). Du brauchst jetzt nur einen Teil des originalen Quadrats, um die verkleinerte Fläche auszulegen? Finde heraus, wie groß ist dieser Anteil ist? Du kannst auch hier eine Kopie des Originalquadrats nutzen. Ergänze die Tabelle.
- Berechne den Flächeninhalt der verkleinerten Quadrate mit Hilfe des gerade ermittelten Anteils und trage ihn in die Tabelle ein.
- Begründe, dass die in a) ermittelte Formel zur Berechnung der Fläche auch für Skalierungsfaktoren k<1 gilt.
Kontrolliere deine Lösung!
- Schiebt man eine Kopie des Originalquadrats auf das verkleinerte Quadrat, erkennt man, dass dass das verkleinerte Quadrat viermal (bzw. achtmal) in das Originalquadrat passen würde. Man benötigt zum Auslegen also nur noch 1/4 bzw. 1/16 der Originalfläche.
- Die Fläche beträgt also 1/4 bzw. 1/16 der Originalfläche.
- Es ist (1/2)² = 1/4, (1/4)²= 1/16 .
Quadratwachstum 2
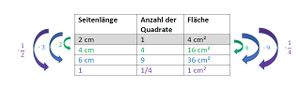
Begründe mit Hilfe des Applets Quadrate 2, dass man mit der gerade entwickelten Idee den Flächeninhalt eines vergrößerten oder verkleinerten Quadrats auch dann berechnen kann, wenn das Originalquadrat eine Seitenlänge von (beispielsweise) 2 cm hat. Gehe dazu folgendermaßen vor:
- Verdopple, verdreifache und halbiere die Seitenlänge des Quadrats. Berechne den Flächeninhalt mit Hilfe der angezeigten Rasterung und trage die Ergebnisse in der Tabelle auf deinem Arbeitsblatt ein.
- Was stellt du fest, wenn du die Zahl der Quadrate (mittlere Spalte) in den beiden Tabellen vergleichst?
- Erkläre in eigenen Worten, wie du die Flächeninhalte der vergrößerten oder verkleinerten Quadrate aus den Flächeninhalt des Originalquadrats und dem Skalierungsfaktor berechnen kannst.
Kontrolliere dann deine Lösung.
Die Anzahl der Quadrate bleibt beim Skalieren gleich. Sie hängt nicht vom Flächeninhalt der Originalfigur ab. Um den Flächeninhalt des vergrößerten oder verkleinerten Rechtecks zu erhalten, muss man den ursprünglichen Flächeninhalt mit der Zahl der Quadrate multiplizieren.
Die Formel für den Flächeninhalt der vergrößerten oder verkleinerten Rechteck ist
Aneu = 2*k².
Ergänze dann nun Lückentext.
Wird die Seitenlänge eines Quadrats
- verdoppelt, so wächst der Flächeninhalt auf das vierfache
- verdreifacht, so wächst der Flächeninhalt auf das neunfache
- verzehnfacht, so wächst der Flächeninhalt auf das hundertfache
- halbiert, so schrumpft der Flächeninhalt auf ein Viertel
Der Flächeninhalt eines Quadrats wächst also quadratisch zum Skalierungsfaktor. Der Flächeninhalt wird berechnet mit Aneu= Aalt*k²
.
Sprinteraufgabe: Gib im Applet Quadrate 2 als neue Seitenlänge 3 cm ein und ermittle den Skalierungsfaktor. Begründe dann mit Hilfe des angezeigten Quadrate, dass die Formel Aneu= A*k² auch für nichtganzzahlige Skalierungsfaktoren gilt.
Beträgt die Seitenlänge des skalierten Quadrats 3 cm, so ist der Skalierungsfaktor k = 1,5.
Die neue Fläche beträgt 9 cm² . Es ist 9 = 4*1,5² = 4 *2,25.
Info
Die Zerlegung des großen Quadrats in kleine Quadrate nennt man auch Rasterung. Mit Hilfe einer solchen Rasterung lassen sich Flächeninhalte berechnen oder zumindest abschätzen.
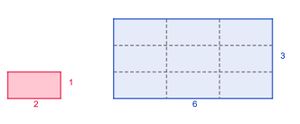
Flächenwachstum von Rechtecken
Auch Rechtecke kann man rastern. Erkläre mit Hilfe der Abbildung, dass auch der Flächeninhalt von Rechtecken bei Skalieren mit dem Faktor k² wächst.
Wie untersucht man das Flächenwachstum krummlinig begrenzter Flächen?
Idee
Krummlinig begrenzte wie Kreise oder Flächen können nicht auf die gleiche Art und Weise gerastert werden. Um zu erkennen, wie sich der Flächeninhalt solcher Flächen verändert, muss die Rastermethode abgewandelt werden. Eine Möglichkeit ist die folgende: Künstler entwerfen großformatige Kunstwerke oft aus kleineren Vorlagen, die sie auf Kästchenpapier zeichen. Anschließend wird das Bild auf vergrößerte Kästchen übertragen.
See
Untersuche, wie der Flächeninhalt des Bildes des Sees beim Vergrößeren wächst. Bearbeite die Aufgaben, die du unter Applet findest.
a) Schätze den Flächeninhalt des Sees durch die Fläche der Kästchen ab. Ein Kästchen hat eine Seitenlänge von 0,5 cm.
a) Der Flächeninhalt des Sees entspricht ca. 22 Kästchen ein. Ein Kästchen hat eine Fläche von 0,25 cm². Also hat der See einen Flächeninhalt von 5,5 cm²
b) KLicke auf "Vergrößere". Schätze genauso den Flächeninhalt des vergrößerten Sees ab. Ein Kästchen hat hier eine Seitenlänge von 1 cm.
b) Der Flächeninhalt des Sees entspricht auch hier ca. 22 Kästchen. Ein Kästchen hat eine Fläche von 1 cm². Also hat der See eine Fläche von 22 cm²
c) Gib den Faktor an, mit dem die Zeichnung skaliert wurde.
c) Der Skalierungsfaktor ist 2, weil die Seitenlängen der Quadrate und somit alle Längen verdoppelt wurden.
Gib an, auf das wievielfache der Flächeninhalt bei der Vergrößerung wächst. Erläutere das Ergebnis mit Hilfe der Graphik. d)Wenn du nicht weiter weißt, kannst du im Applet auf Hilfe klicken.
d) Der Flächeninhalt wächst auf das Vierfache. Erklärung: Die Seitenlänge der Quadrate hat sich verdoppelt, also vervierfacht sich der Flächeninhalt der Quadrate. Da beim Skalieren das Verhältnis von Flächeninhalt zueinander gleichbleibt, vervierfacht sich auch der Flächeninhalts des Sees.
Hinweis: Dies sieht man auch, wenn man Flächen aus a und b miteinander vergleicht.
e) Wie groß wäre der Flächeninhalts des Sees, wenn die Kästchen eine Seitenlänge von 10 cm hätten?
Überlege, mit welchem Faktor die Seitenlängen (ausgehend von der Originalzeichnung) skaliert wurden. Nutze dann dein Wissen über das Wachstum von Flächen.
e) Der Skalierungsfaktor beträgt 20. Der Flächeninhalts wächst also auf das 400fache. Also beträgt der Flächeninhalt des Sees 5,5 cm²*400 = 2200 cm²
{{Box|]Wachstum von Flächeninhalten beim Skalieren|[[Datei:MerksatzFlächen.jpg|200px|left]Beim Skalieren mit dem Faktor k wachsen (oder schrumpfen) Flächeninhalte mit dem Faktor k²|Merksatz}}
Idee
Mit Hilfe des Skalierungsfaktors kannst du die Flächeninhalte beliebiger vergrößerter oder verkleinerter Figuren sehr schnell berechnen
Flächeninhalte schnell berechnen
Berechne die neuen Flächeninhalte mit Hilfe des Skalierungsfaktors:
- Ein Quadrat hat einen Flächeninhalt von 32 cm². Welchen Flächeninhalt das ein Quadrat, dass mit dem Faktor 1/4 verkleinert wurde.
- Ein Kreis hat einen Flächeninalt von 10 cm². Welchen Flächeninhalt hat ein Kreis, der mit dem Faktor fünf vergrößert wurde?
- Die abgebildete Eule hat einen Flächeninhalt von 0,25 m². Welchen Flächeninhalt hat das mit dem Faktor 3 vergrößerte Bild der Eule?
- Eine rechteckige Tischdecke hat eine Fläche von 0,6 m². Welche Fläche hat eine rechteckige Tischdecke, deren Seitenlängen doppelt so lang sind?
- Eine Riesenpizza hat eine Fläche von 2000 cm². Welche Fläche hat eine Pizza, deren Durchmesser nur halb so groß ist?
- (1/4)²=1/16. 32* 1/16= 2. Das Quadrat hat einen Flächeninhalt von 2 cm³
- 5² = 25. 10*25 = 250. Der Kreis hat einen Flächeninhalt von 250 cm².
- 3² = 9. 0,25*9=2,25. Die vergrößerte Eule hat einen Flächeninhalt von 2,25 m²
- Der Skalierungsfaktor ist 2; 2²= 4. 0,6*4 = 2,4. Die Tischdecke hat einen Flächeninhalt von 2,4 m².
- Der Skalierungsfaktor ist 0,5. 0,5² = 0,25. 2000*0,25 = 500. Die Pizza hat eine Fläche von 500 cm².
Material für das Teeservice
Die Untertasse des originalen Teeservies hat eine Fläche von hat eine Fläche von 180 cm², die Oberfläche der Teetasse beträgt 210 cm².
Berechne die Fläche der vergrößerten Untertasse und die Oberfläche der vergrößerten Teetasse.
Da die Gegenstände mit dem Faktor 10 vergrößert wurden, wachsen die Flächen auf das Hundertfache. Die Untertasse hat also eine Fläche von 180*100 = 18000 cm². Dies sind 1,8 m² , die Teetasse hat eine Oberfläche von 210*100 = 21000 cm². Das sind 2,1m²
3. So wachsen Volumen von Objekten beim Vergrößern und Verkleinern
Idee
Auch für das Volumen von Körpern gibt es eine Gesetzmäßigkeit, mit der die Volumen beim Vergrößern oder Verkleinern wachsen bzw. schrumpfen. Diese Gesetzmäßigkeit sollst du am Beispiel eines Würfels erarbeiten:
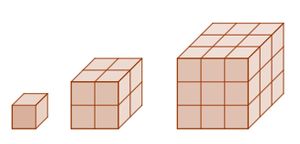
Würfelwachstum
Der kleine Würfel hat eine Seitenlänge von 1 cm. Der zweite und dritte Würfel entstehen, indem kleine Würfel aneinandergeklebt werden.
- Trage zunächst die Seitenlängen und den Flächeninhalt der Seiten des zweiten und dritten Würfels in auf der Tabelle in deinem Arbeitsblatt ein.
- Überlege dann, welches Volumen der zweite und dritte Würfel haben. Trage die Werte in die Tabelle ein.
- Ergänze die Werte für den "Viererwürfel".
- Erkläre mit Hilfe der Tabelle, wie das Volumen eines beliebigen Würfels wächst, wenn man die Seitenlänge des Würfels verdoppelt bzw. verdreifacht.
Kontrolliere dein Ergebnis.
- Ergänze dann den Lückentext
Wenn man die Seitenlängen eines Würfels
- verdoppelt, so wächst das Volumen auf das achtfache
- verdreifacht, so wächst der Flächeninhalt auf das siebenundzwanzigfache
- verzehnfacht, so wächst der Flächeninhalt auf das hundertfache
- halbiert, so schrumpft der Flächeninhalt auf ein Achtel
Skaliert man einen Würfel mit dem Faktor k, so ist das neue Volumen Vneu= Valt*k³
.
Idee
Dieses Wachstumsprinzip gilt für beliebige Körper. Man kann alle Überlegungen zu den Flächen auf den "3D-Fall" übertragen.
Wie wachsen Volumina
Bei Skalieren eines Körpers mit dem Faktor k wachsen oder schrumpfen Volumina mit dem Faktor k³.
Idee
Auch das Volumina lassen sich beim Vergrößern und Verkleinern schnell mit Hilfe des Skalierungsfaktors berechnen.
Volumina schnell berechnen
Berechne die neuen Volumina mit Hilfe des Skalierungsfaktors:
- in Würfel hat ein Volumen von 8cm³. Welches Volumen hat ein mit dem Faktor 0,5 verkleinerter Würfel?
- Tom hat Glasmurmeln verschiedener Größen. Die kleinste Glasmurmel wiegt 4 Gramm. Wie schwer ist die größte Murmel, deren Durchmesser fünfmal so groß ist?
- Ein quaderförmiges Aquarium hat ein Volumen von 640 l. Welches Volumen hat ein Aquarium, dessen Seitenlängen viermal so lang sind?
- 0,5³= 0,125 8*0,125= 1. Der Würfel hat ein Volumen von 1 cm³
- Der Skalierungsfaktor ist 5. 5³=125. 4*125= 500 Die größte Murmel wiegt 500 g.
- Skalierungsfaktor ist 3. 3² = 9. 0,25*9=2,25. Die vergrößerte Eule hat einen Flächeninhalt von 2,25 m²
Eine Riesenmenge Tee?
In eine normale Teetasse passen 150 ml Tee. Berechne, wieviel Tee in die vergrößerte Version der Teetasse passen würde.
150000 ml= 150 l
4. Zusammenfassung
Zusammenfassung: So verändern sich Längen, Flächeninhalte und Volumina beim Skalieren
Lückentext oder Bild?
Das Riesenschachbrett.
Die geschrumpfte Alice muss gegen Schachfiguren kämpfen. Für das Set musste eine entsprechend großes Schachbrett angefertigt werden.
In der Tabelle findest du Angaben zum originalen Schachbrett. Gib den Skalierungsfaktor an und berechne dann alle Maße und Gewichte für das vergrößerte Schachbrett. Trage alle Ergebnisse in die Tabelle auf deinem Arbeitsblatt ein.
Kontrolliere anschließend deine Lösung.