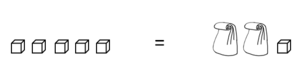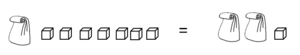Benutzer:Buss-Haskert/Gleichungen/Was ist eine Gleichung: Unterschied zwischen den Versionen
KKeine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
(Übungen ergänzt) Markierung: 2017-Quelltext-Bearbeitung |
||
| Zeile 113: | Zeile 113: | ||
[[Datei:Tabellenblatt Lösung Einstiegsaufgabe.png|rahmenlos]]|Lösung|Verbergen}} | [[Datei:Tabellenblatt Lösung Einstiegsaufgabe.png|rahmenlos]]|Lösung|Verbergen}} | ||
{{Box|Übung 7 - Lösen mit einer Tabellenkalkulation|Löse die | {{Box|Übung 7 - Lösen mit einer Tabellenkalkulation|Löse die Aufgaben aus dem Buch mit einer Tabellenkalkulation. Lade deine Datei im Modul Aufgaben hoch. | ||
* S. 116 Nr. 7 | * S. 116 Nr. 7 | ||
* S. 116 Nr. 11|Üben}} | * S. 116 Nr. 11|Üben}} | ||
===1.3 Anwendungsaufgaben=== | ===1.3 Anwendungsaufgaben=== | ||
Es gibt verschiedene Bereiche, in denen Gleichungen Anwendung finden: | |||
[[Datei:Anwendungsbereiche Gleichungen.png|rahmenlos|800px]]<br> | |||
<br> | |||
'''<big>Bist du fit? Vorübungen</big>''' | |||
<br> | |||
====Mathematische Texte==== | |||
{{Box|Vorübung: Mathematische Texte|Um Zahlenrätsel lösen zu können, musst du die Fachbegriffe kennen. Übe dies im nachfolgenden Quiz|Üben}} | |||
<div class="lueckentext-quiz"> | |||
Addition: '''1. Summand''' + '''2. Summand''' = Wert der'''Summe'''<br> | |||
Subtraktion: '''Minuend''' - '''Subtrahend''' = Wert der '''Differenz'''<br> | |||
Multiplikation: '''1. Faktor''' ∙ '''2. Faktor''' = Wert des '''Produktes'''<br> | |||
Division: '''Dividend''': '''Divisor''' = Wert des '''Quotienten''' | |||
</div> | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
|Addition||addieren||vermehren||plus | |||
|- | |||
|Subtraktion||subtrahieren||vermindern||minus | |||
|- | |||
|Multiplikation||multiplizieren||verdoppeln||vervielfachen||mal | |||
|- | |||
|Division||dividieren||halbieren||teilen||geteilt | |||
|} | |||
</div> | |||
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme. | |||
{{Box|Übung 8|Löse die Aufgaben aus dem Buch. Gib zunächst die Bedeutung der Variablen an, stelle dann die Terme passend zum Text auf. Notiere eine Gleichung und löse diese durch Probieren. | |||
* S. 115 Nr. 5 | |||
* S. 116 Nr. 10|Üben}} | |||
<br /> | |||
====Geometrische Anwendungen==== | |||
{{Box|Vorübung 2: Geometrische Anwendungen|Anwendungsaufgaben aus dem Bereich Geometrie erfordern Kenntnisse über verschiedene Figuren. Löse das nachfolgende Quiz zur Wiederholung.|Üben}} | |||
<div class="zuordnungs-quiz"> | |||
{| | |||
|Quadrat||[[Datei:Quadrat.png|ohne|70px]]||u = 4·a||A = a² | |||
|- | |||
|Rechteck||[[Datei:Rechteck.png|ohne|70px]]||u = 2a + 2b||A = a·b | |||
|- | |||
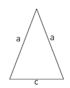
|gleichschenkliges Dreieck||[[Datei:Gleichschenkliges Dreieck.png|ohne|70px]]||u = 2a + c||2 gleich lange Seiten||α+β+γ=180° | |||
|- | |||
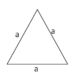
|gleichseitiges Dreieck||[[Datei:Gleichseitiges Dreieck.png|ohne|70px]]||u = 3a||3 gleich lange Seiten||α+β+γ=180° | |||
|} | |||
</div> | |||
{{LearningApp|app=pgc1th79520|width=100%|height|400px}} | |||
<br> | |||
{{Box|Übung 9|Löse die Aufgabe aus dem Buch. Gib zunächst die Bedeutung der Variablen an, stelle dann die Terme passend zum Text auf. Notiere eine Gleichung und löse diese durch Probieren. | |||
* S. 116 Nr. 13|Üben}} | |||
====Sachsituationen==== | |||
{{Box|Vorübung 3: Sachsituationen|Ordne in der nachfolgen den Termen die passende Bedeutung zu.|Üben}} | |||
{{LearningApp|app=p8yuzo3dj20|width=100%|height=500px}} | |||
In allen Anwendungsbereichen ist es wichtig, dass du den Text '''genau liest''', dir die Situation vorstellst und mit eigenen Worten beschreibst. | |||
{{Box|Übung 10|Löse die Aufgaben aus dem Buch. Gib zunächst die Bedeutung der Variablen an, stelle dann die Terme passend zum Text auf. Notiere eine Gleichung und löse diese durch Probieren. | |||
* S. 115 Nr. 6 a-d | |||
|Üben}} | |||
__INHALTSVERZEICHNIS_ERZWINGEN__ | __INHALTSVERZEICHNIS_ERZWINGEN__ | ||
Version vom 30. März 2021, 08:00 Uhr
SEITE IM AUFBAU!!
1.1) Was ist eine Gleichung?
Kennst du eine Balkenwaage z.B. aus dem Physikunterricht oder vom Markt?
 oder
oder 
Diese Waagen sind im Gleichgewicht, wenn das Gewicht auf beiden Seiten der Waage gleich groß ist.
In der Mathematik liegt auf jeder Seite der Waage ein Term (Rechenausdruck). Das Gleichgewicht stellen wir mit einem Gleichheitszeichen dar.
Du kennst Terme (Rechenausdrücke) aus dem vorangegangenen Kapitel. Nun verbindest du zwei Terme durch ein Gleichheitszeichen. Damit erhältst du eine Gleichung.
Ziel ist es, für die Variablen genau die Zahl zu finden, sodass auf beiden Seiten der Gleichung derselbe Wert steht. Dann ist die Waage im Gleichgewicht.
In jeder Tüte befinden sich gleich viele Klötzchen (x-Stück).
Wie viele Klötzchen befinden sich in jeder Tüte, damit die Waage im Gleichgewicht ist?

1.2 Lösen durch Probieren
Die Gleichung zur Situation lautet:
Du setzt die Werte für x immer anstelle der Variablen ein. Dann rechnest du die beiden Seiten der Gleichung aus und prüfst, ob sie denselben Wert haben. Wenn dies der Fall ist, hast du die Lösung der Gleichung gefunden.
Beispiel:
x + 7 = 2·x + 1 für x = 2
2 + 7 = 2·2 + 1
9 = 5 (f)
Lösung der Gleichung:
x = 6, denn
x + 7 = 2·x + 1 für x = 6
6 + 7 = 2·6 + 1
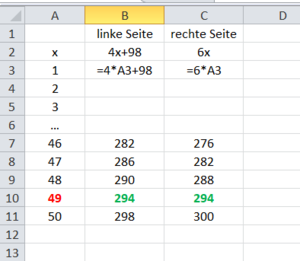
Die Lösung einer Gleichung kann durch Probieren bestimmt werden:
Setze dazu für x verschiedene Zahlen ein. Prüfe, ob eine wahre(w) oder falsche(f) Aussage entsteht.
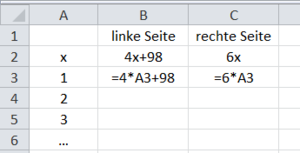
Du benötigst 3 Spalten:
Spalte A: Werte von x; Spalte B: Wert der linken Seite der Gleichung; Spalte C: Wert der rechten Seite der Gleichung
1.3 Anwendungsaufgaben
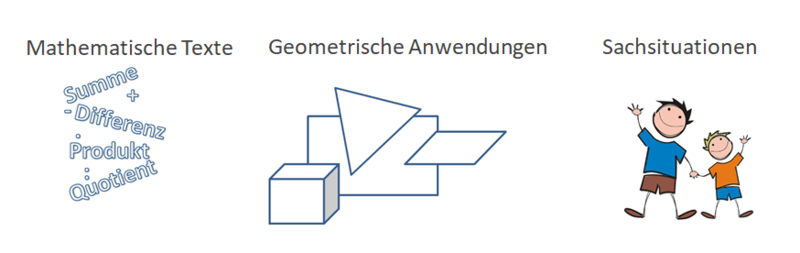
Es gibt verschiedene Bereiche, in denen Gleichungen Anwendung finden:
Bist du fit? Vorübungen
Mathematische Texte
Addition: 1. Summand + 2. Summand = Wert derSumme
Subtraktion: Minuend - Subtrahend = Wert der Differenz
Multiplikation: 1. Faktor ∙ 2. Faktor = Wert des Produktes
Division: Dividend: Divisor = Wert des Quotienten
| Addition | addieren | vermehren | plus | |
| Subtraktion | subtrahieren | vermindern | minus | |
| Multiplikation | multiplizieren | verdoppeln | vervielfachen | mal |
| Division | dividieren | halbieren | teilen | geteilt |
Schreibe über den Aufgabentext die passenden Rechenzeichen. Dies hilft dir beim Aufstellen der Terme.
Geometrische Anwendungen
| Quadrat | u = 4·a | A = a² | ||
| Rechteck | u = 2a + 2b | A = a·b | ||
| gleichschenkliges Dreieck | u = 2a + c | 2 gleich lange Seiten | α+β+γ=180° | |
| gleichseitiges Dreieck | u = 3a | 3 gleich lange Seiten | α+β+γ=180° |
Sachsituationen
In allen Anwendungsbereichen ist es wichtig, dass du den Text genau liest, dir die Situation vorstellst und mit eigenen Worten beschreibst.