Abitur Physik am Gymnasium Trittau/Größen: Unterschied zwischen den Versionen
GT065 (Diskussion | Beiträge) Keine Bearbeitungszusammenfassung Markierung: 2017-Quelltext-Bearbeitung |
(Grafik erneuert) |
||
| (5 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
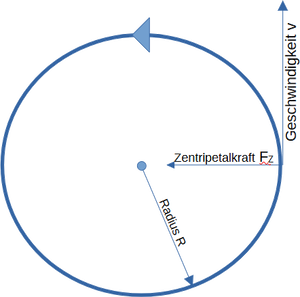
[[Datei:Kreisbewegung.png|mini|Kreisbahn mit Vektoren für Geschwindigkeit, Kraft und Radius]] | |||
Eine Kreisbewegung setzt sich aus mehreren Faktoren zusammen. Mithilfe dieser Faktoren lässt sich die Kreisbahn beschreiben, als auch deren verschiedenen Faktoren zu berechnen. Somit gibt es auch verschiedene Formeln die dabei zur Anwendung kommen. Diese lauten: | Eine Kreisbewegung setzt sich aus mehreren Faktoren zusammen. Mithilfe dieser Faktoren lässt sich die Kreisbahn beschreiben, als auch deren verschiedenen Faktoren zu berechnen. Somit gibt es auch verschiedene Formeln die dabei zur Anwendung kommen. Diese lauten: | ||
<math>v={2 \pi \cdot r\over T} = 2\pi \cdot r \cdot f= \omega \cdot r</math> ; <math>a_{r}={v^2\over r}= \omega \cdot r^2</math> und <math>a_{r}= {4\pi \cdot r\over T^2}</math> , dabei beschreibt v die Geschwindigkeit und a<sub>r</sub> die [[Abitur Physik am Gymnasium Trittau/Zentripetalkraft|Zentripetalkraft]]. | <math>v={2 \pi \cdot r\over T} = 2\pi \cdot r \cdot f= \omega \cdot r</math> ; <math>a_{r}={v^2\over r}= \omega \cdot r^2</math> und <math>a_{r}= {4\pi \cdot r\over T^2}</math> , dabei beschreibt v die Geschwindigkeit und a<sub>r</sub> die Zentripetalbeschleunigung, die aus der [[Abitur Physik am Gymnasium Trittau/Zentripetalkraft|Zentripetalkraft]] folgt. | ||
Diese Formeln können nur auf eine Gleichförmige Kreisbewegung angewendet werden. Die Kreisbewegung kann durch die [[Abitur Physik am Gymnasium Trittau/Zentripetalkraft|Zentripetalkraft]] entstehen. | Diese Formeln können nur auf eine Gleichförmige Kreisbewegung angewendet werden. Die Kreisbewegung kann durch die [[Abitur Physik am Gymnasium Trittau/Zentripetalkraft|Zentripetalkraft]] entstehen. | ||
Aktuelle Version vom 12. März 2024, 19:03 Uhr
Eine Kreisbewegung setzt sich aus mehreren Faktoren zusammen. Mithilfe dieser Faktoren lässt sich die Kreisbahn beschreiben, als auch deren verschiedenen Faktoren zu berechnen. Somit gibt es auch verschiedene Formeln die dabei zur Anwendung kommen. Diese lauten:
Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle v={2 \pi \cdot r\over T} = 2\pi \cdot r \cdot f= \omega \cdot r} ; Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a_{r}={v^2\over r}= \omega \cdot r^2} und Fehler beim Parsen (SVG (MathML kann über ein Browser-Plugin aktiviert werden): Ungültige Antwort („Math extension cannot connect to Restbase.“) von Server „https://en.wikipedia.org/api/rest_v1/“:): {\displaystyle a_{r}= {4\pi \cdot r\over T^2}} , dabei beschreibt v die Geschwindigkeit und ar die Zentripetalbeschleunigung, die aus der Zentripetalkraft folgt.
Diese Formeln können nur auf eine Gleichförmige Kreisbewegung angewendet werden. Die Kreisbewegung kann durch die Zentripetalkraft entstehen.