Spielwiese
Schreiben im Wiki
Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Vorlagen
Das ist ein Tipp.
Das ist eine Lösung.
Aufgabe 1:Münzwurf
Wirf eine Münze 3 Mal.
Merksatz: Kongruenzsätze
beliebiger Inhalt.
Beispiel: Polynomdivision
beliebiger Inhalt.
Dateien
Über die Bedienelemente
Lorem ipsummmmmmmmmmmmmmm mmmmmmm mmmmmmmm
Lorem ipsum
Mittels Quelltexteingabe (Ohne Umfließen des Textes)
Lorem ipsum
Lorem ipsum
Über Wikipedia (Ohne Rahmen)
Lorem ipsum
 Lorem ipsum
Lorem ipsum
Interaktive Applets
LearningApp
GeoGebra
<ggb_applet id="EHBuqva8" width="1000" height="269" />
H5p
{{H5p-zum|id=21617|height=600}}
Tabelle Ecken, Kanten Flächen Pyramide
Du hast bereits gelernt, dass eine Pyramide verschiedene Vielecke als Grundfläche haben kann. Dadurch unterscheiden sich die Pyramiden in der Anzahl der Ecken, Kanten und Flächen.
Aufgabe 1: Pyramiden vergleichen
Wie viele Ecken, Kanten und Flächen besitzt eine Pyramide mit einem 3-Eck, 4-Eck, 8-Eck und 10-Eck als Grundfläche? Wechsle dazu zu deinem Arbeitsblatt und vervollständige die Tabelle.
Hier siehst du eine Pyramide mit einem Dreieck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung.
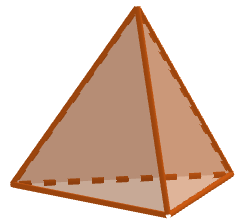
Pyramide mit Dreieck als Grundfläche
Die Grundfläche der Pyramide hat 3 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 4 Ecken.
Die Grundfläche der Pyramide hat 3 Kanten. Dazu kommen 3 Seitenkanten. Insgesamt hat die Pyramide also 6 Kanten.
Die Pyramide hat eine Grundfläche. Hinzu kommen 3 Seitenflächen. Insgesamt hat die Pyramide also
4 Flächen.
Hier siehst du eine Pyramide mit einem Viereck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung.
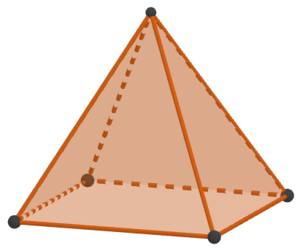
Pyramide mit Viereck als Grundfläche
Die Grundfläche der Pyramide hat 4 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 5 Ecken.
Die Grundfläche der Pyramide hat 4 Kanten. Dazu kommen 4 Seitenkanten. Insgesamt hat die Pyramide also 8 Kanten.
Die Pyramide hat eine Grundfläche. Hinzu kommen 4 Seitenflächen. Insgesamt hat die Pyramide also
5 Flächen.
Hier siehst du eine Pyramide mit einem Achteck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung.
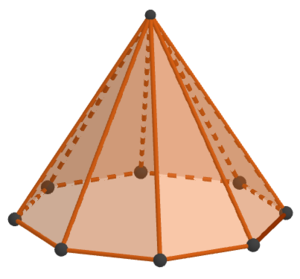
Pyramide mit Achteck als Grundfläche
Die Grundfläche der Pyramide hat 8 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 9 Ecken.
Die Grundfläche der Pyramide hat 8 Kanten. Dazu kommen 8 Seitenkanten. Insgesamt hat die Pyramide also 16 Kanten.
Die Pyramide hat eine Grundfläche. Hinzu kommen 8 Seitenflächen. Insgesamt hat die Pyramide also
9 Flächen.
Hier siehst du eine Pyramide mit einem Zehneck als Grundfläche. Bestimme die Anzahl der Ecken, Kanten und Flächen mithilfe der Abbildung.
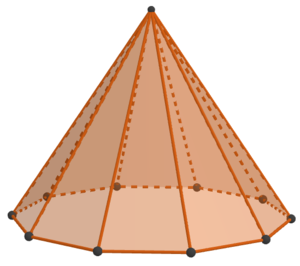
Pyramide mit Zehneck als Grundfläche
Die Grundfläche der Pyramide hat 10 Ecken. Hinzu kommt die Ecke der Spitze. Insgesamt hat die Pyramide somit 11 Ecken.
Die Grundfläche der Pyramide hat 10 Kanten. Dazu kommen 10 Seitenkanten. Insgesamt hat die Pyramide also 20 Kanten.
Die Pyramide hat eine Grundfläche. Hinzu kommen 10 Seitenflächen. Insgesamt hat die Pyramide also
11 Flächen.
*Besondere Pyramiden
Aufgabe 1: Besondere Pyramiden
Nachdem du dir die Definition einer Pyramide erarbeitet hast, kannst du dieses Wissen in der nächsten Aufgabe anwenden. Wechsle nun zu deinem Arbeitsblatt und bearbeite Aufgabe ?.
Schaue dir die Grundfläche und die Seitenflächen des Körpers an.
Pyramiden haben ein Vieleck als Grundfläche und Dreiecke als Seitenflächen. Außerdem treffen sich die Seitenflächen in einem Punkt, die Spitze. Erfüllt der Körper diese Kriterien?
Bei dem Körper handelt es sich um eine Pyramide. Die Grundfläche ist ein Fünfeck und damit ein Vieleck. Der Körper wird von Dreiecken begrenzt. Außerdem treffen sich die Seitenflächen in einem Punkt. Diese Pyramide ist besonders, da sich die Spitze nicht über dem Mittelpunkt der Grundfläche befindet. Deshalb nennt man diese Pyramide eine schiefe Pyramide.
Bei dem Körper handelt es sich um eine Pyramide mit quadratischer Grundfläche. Außerdem bestehen die Seitenflächen aus Dreiecken, die sich in einem Punkt treffen. Das Besondere an dieser Pyramide ist, dass sie nicht auf ihrer Grundfläche steht, sondern auf einer Seitenfläche liegt.
Bei dem Körper handelt es sich nicht um eine Pyramide, da die Grundfläche ein Kreis und damit kein Vieleck ist. Außerdem sind die Seitenflächen keine Dreiecke. Dieser Körper ist ein Kegel.
Bei dem Körper handelt es sich um eine Pyramide. Die Grundfläche ist ein Sechseck und damit ein Vieleck. Außerdem bestehen die Seitenflächen aus Dreiecken, die sich in einem Punkt treffen. Da die Grundfläche unregelmäßig ist, spricht man von einer unregelmäßigen Pyramide.










