3 Exponentielles Wachstum
Einstieg: Weltbevölkerung
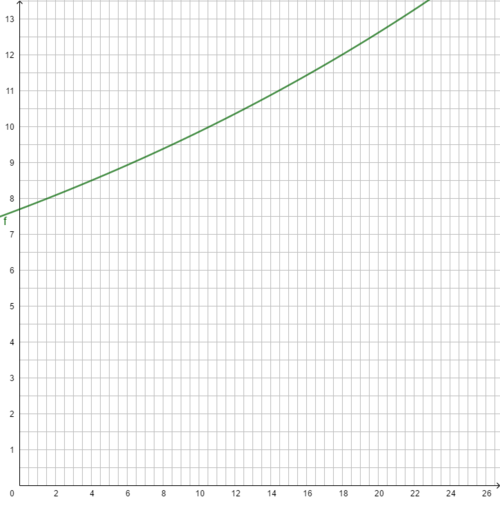
Im Jahr 2019 lebten 7,7 Mrd. Menschen auf der Erde. Wissenschaflter prognostizierten in diesem Jahr eine jährliche Zuwachsrate von 1,25%.
Also gilt q=100%+1,25% = 101,25% = 1,0125
Wie viele Menschen leben demnach im Jahr 2030 auf der Erde?
Stelle diese Situation auf verschiedene Arten dar. (Erinnerung: Text (ist gegeben), Wertetabelle, Funktionsgleichung und Funktionsgraph)
Prognose für das Jahr 2030: n = 11
W11 = W0 ∙ q11
= 7,70 ∙ 1,02511
≈8,83
Exponentielles Wachstum - Exponentialgleichung
Wir sprechen von exponentiellem Wachstum, wenn der Wert einer Größe in gleichen Zeitspannen immer um denselben Prozentsatz p% zunimmt bzw. abnimmt.
Die neue Größe nach n Zeitspannen berechnen wir mit
Wn = W0 · qn,
wobei q der Wachstumsfaktor ist. q = 1+p% (Zunahmen) bzw.q=1-p%(Abnahme)
Die Gleichung Wn = W0 · qn heißt Exponentialgleichung, da die Variable n im Exponenten steht.
Anwendungsaufgabe 1: Erdbevölkerung
...(Anwendung, Wn gesucht)
Anwendungsaufgabe 2: Klimawandel
...(Anwendung W0 gesucht)
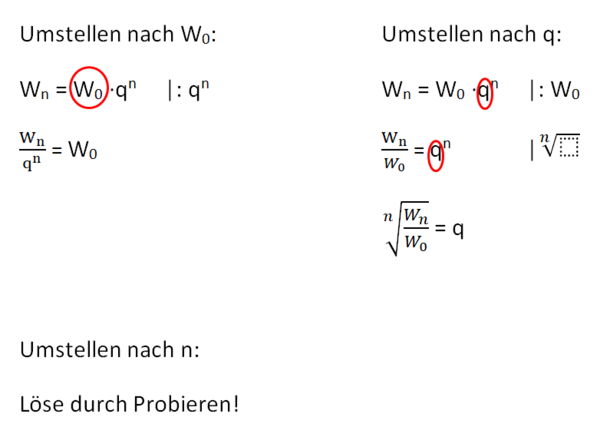
Exponentialgleichung - Formel umstellen
Anwendungsaufgabe 3
...(Anwendung q gesucht)
Anwendungsaufgabe 4
...(Anwendung n gesucht)
ÜBUNGSAUFGABEN ERGÄNZEN
- Formel umstellen
- Verdopplungszeit (Bakterien)
Applet von Hegius, R. Schürz
Applet von Hegius, R. Schürz
4 Die Exponentialfunktion
Exponentialfunktion
Die Funktion mit der Gleichung f(x) = c∙ax heißt Exponentialfunktion.
Eigenschaften der Exponentialfunktion
Beschreibe die Eigenschaften der Exponentialfunktion f(x) = c∙ax .
Wähle zunächst c=1. Wie verläuft der Graph der Funktion? Löse den Lückentext und übertrage ihn in dein Heft.
Applet von Ralf Wagner
Der Graph verläuft immer oberhalb der x-Achse.
Der Graph geht immer durch den Punkt (0|1).
Für a>1 steigt der Graph (Zunahme),
für 0<a<1
fällt der Graph (Abnahme).