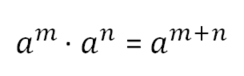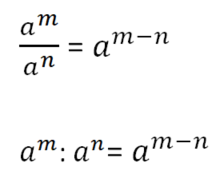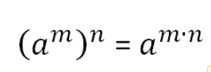SEITE IM AUFBAU !!!
2) Potenzgesetze 2.1) Potenzen mit gleicher Basis 33 ∙ 34 = 3∙3∙3 ∙ 3∙3∙3∙3 = 37 2 ∙ 53 = ______________ = 5_ 2 ∙ a4 = __________________ = a_
3
5
:
3
3
=
3
5
3
3
=
3
⋅
3
⋅
3
⋅
3
⋅
3
3
⋅
3
⋅
3
=
3
2
{\displaystyle 3^5:3^3 = \tfrac{3^5}{3^3} = \tfrac{3\cdot3\cdot3\cdot3\cdot3}{3\cdot3\cdot3} = 3^2}
5
6
:
5
2
=
5
6
5
2
=
{\displaystyle 5^6:5^2 = \tfrac{5^6}{5^2} =}
a
5
:
a
2
=
a
5
a
2
=
{\displaystyle a^5:a^2 = \tfrac{a^5}{a^2} =}
(von TTraub)
Löse auf der Seite Aufgabenfuchs
Aufgabe Nr. 8, 9, 10, 11, 12
Aufgabe Nr. 17, 18
Potenzen mit gleicher Basis werden multipliziert, indem man die Exponenten addiert und die Basis beibehält.
Schreibe die Aufgabe ab und löse mithilfe der Potenzgesetze.
S. 57 Nr. 1
S. 57 Nr. 3a,b
S. 57 Nr. 4a-c
Schreibe die Aufgabe ab und löse.
S. 57 Nr. 4 d,e
S. 57 Nr. 9
Potenzen mit gleicher Basis werden dividiert, indem man die Exponenten subtrahiert und die Basis beibehält.
Schreibe die Aufgabe ab und löse mithilfe der Potenzgesetze.
S. 57 Nr. 1
S. 57 Nr. 3c,d
S. 57 Nr. 5 a-c
S. 57 Nr. 8
Schreibe die Aufgabe ab und löse.
Potenzen werden potenziert, indem man die Exponenten multipliziert und die Basis beibehält.
Schreibe die Aufgabe ab und löse mithilfe der Potenzgesetze.
S. 58 Nr. 19
S. 58 Nr. 20
Schreibe die Aufgabe ab und löse.
S. 58 Nr. 21
S. 58 Nr. 22
2.2) Potenzen mit gleichem Exponenten
(von TTraub)
2.3) Potenzen potenzieren 2.4) Potenzen mit negativen Exponenten Vermischte Übungen
(von hz)