Benutzer:Buss-Haskert/Vierecke und Dreiecke/Umfang und Flächeninhalt/Parallelogramm

4.4) Raute: Umfang und Flächeninhalt

Die Raute ist ein besonderes Parallelogramm, also gelten auch die Formeln des Parallelogramms für die Raute.

Es gibt eine weitere Möglichkeit, den Flächeninhalt einer Raute zu bestimmen. Bearbeite dazu das Applet. Findest du eine Formel für den Flächeninhalt?

Flächeninhalt und Umfang einer Raute

Die Raute ist ein besonderes Parallelogramm. Daher ist der Flächeninhalt A einer Raute:
A = a∙h_a

Sind e und f die Diagonalen der Raute gilt zudem:

A = $\frac{\text{e*f}}{\text{2}}$

Der Umfang u einer Raute wird berechnet mit

u = 4a .

Übung 7

Löse Buch

• S. 96 Nr. 5c

Tipp 1 zu Nr. 5c

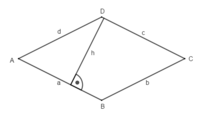
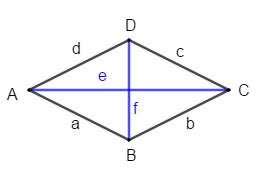
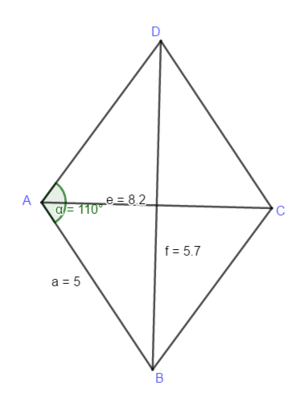
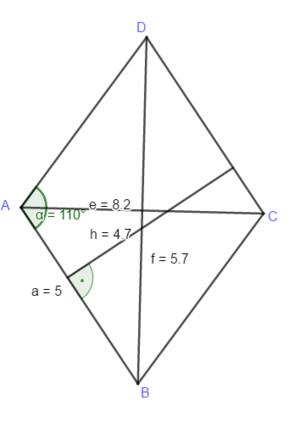
Zeichne die Diagonalen ein und miss ihre Länge. Berechne damit den Flächeninhalt.
Du kannst deine Rechnung prüfen, wenn du die auch die Höhe einer Seite einzeichnest, misst und dann mit der Flächeninhaltesformel für das Parallelogramm berechnest. Die Flächeninhalte müssen gleich sein.

Tipp 2 zu Nr. 5c

4.5) Trapez: Umfang und Flächeninhalt

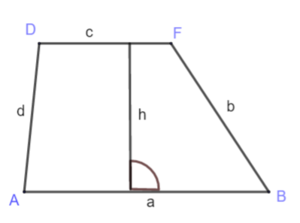
Flächeninhalt und Umfang des Trapezes

Sind die a und c die parallelen Seiten des Trapezes und h die Höhe, wird der Flächeninhalt A eines Trapezes so berechnet:
A = $\frac{\text{(a+c)h}}{\text{2}}$ oder A = $\frac{\text{(a+c)}}{\text{2}}$∙h

Der Umfang u eines Trapezes wird berechnet mit

u = a + b + c + d.

Übung 8

Löse Buch

• S. 92 Nr. 1
• S. 92 Nr. 2a,c

Umstellen der Formel

Um die Länge einer der Seiten a und c oder der Höhe zu berechnen, muss die Formeln für den Flächeninhalt umgestellt werden.
1. Stelle die Flächeninhaltsformel um nach den Seitenlängen a und c.

2. Stelle die Flächeninhaltsformel nach der Höhe um.

Umstellen nach der Seite a:

$\frac{\text{a+c}}{\text{2}}$∙h   |∙2
2∙A = (a+c)∙h   |:h
$\frac{\text{2A}}{\text{h}}$ = a+c   |-c
$\frac{\text{2A}}{\text{h}}$ - c = a

Stelle die Formel entsprechend nach c um.

Umstellen nach der Höhe:

$\frac{\text{a+c}}{\text{2}}$∙h   |∙2
2∙A = (a+c)∙h   |:(a+c)
$\frac{\text{2A}}{\text{a+c}}$ = h

Übung 9

Löse Buch

• S. 92 Nr. 5
• S. 96 Nr. 4

Notiere die Formel und stelle sie nach der gesuchten Größe um. Setze dann ein und berechne.

Übung 10: Anwendungsaufgaben zu Trapezen

Löse die Anwendungsaufgaben übersichtlich. Notiere zunächst die gegebenen Größen. Zeichne eine Skizze und beschrifte diese. Überlege, was gesucht ist. Unterscheide zwischen Flächeninhalt A(innen drin) und Umfang u (drum herum).

• S. 92 Nr. 6
• S. 92 Nr. 7
• S. 92 Nr. 8

Tipp zu Nr. 6

Der Querschnitt des Kanals hat die Form eines Trapezes. Zeichne eine Skizze in dein Heft und beschrifte sie mit den angegebenen Maßen.

Gesucht ist die Querschnittsfläche.
Lösung: 1386m²

Tipp 1 zu Nr. 7

Die gesamte Fläche der Backform setzt sich aus 5 Teilflächen zusammen:
Der Boden ist ein Rechteck.
Die Seiten der Backform sind jeweils Trapeze.
Skizziere die Flächen jeweils und beschrifte sie mit den angegebenen Maßen.

Lösung: 671 cm²

Tipp 2 zu Nr. 7

Zugabe von 10%
geg: G = 671cm²; p% = 10% = 0,1; p⁺%=110%=1,1
ges: G⁺

G⁺=G∙p⁺%

Tipp zu Nr. 8

Die Fläche des Steins entspricht der Fläche des großen Rechtecks minus den 2 kleinen Trapezflächen. Zeichne eine Skizze in dein Heft und beschrifte sie vollständig. Berechne dann die Fläche eines Steines.
Bestimme damit die Anzahl der Steine pro 1m² (=10000cm²).
Lösung: AStein=265cm²; ca.38 Steine

4.6) Dreieck: Umfang und Flächeninhalt

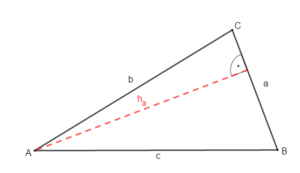
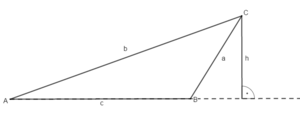
Wiederhole zunächst die Bezeichnungen am Dreieck. Übertrage die Zeichnung in dein Heft.

Verschiebe im nachfolgenden Applet die Punkte und beobachte die Lage der Höhen. Was fällt dir auf?

Tipp zur Lage der Höhen

Die Höhen stehen senkrecht auf den Dreiecksseiten und verlaufen durch den gegenüberliegenden Eckpunkt.
Die Höhen schneiden sich in einem Punkt.

In einem stumpfwinkligen Dreieck verlaufen zwei Höhen außerhalb des Dreiecks.

Höhen im Dreieck zeichnen

Zeichne ein beliebiges Dreieck in dein Heft und beschrifte es. Zeichne nun die Höhen h_a, h_b und h_c ein. Die Bildfolgen helfen dir dabei.

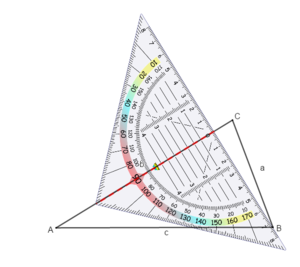
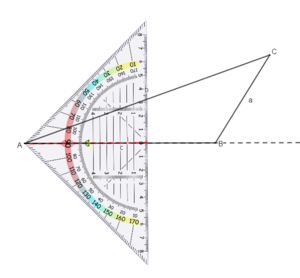
Zeichne die Höhe h_c zur Seite c:

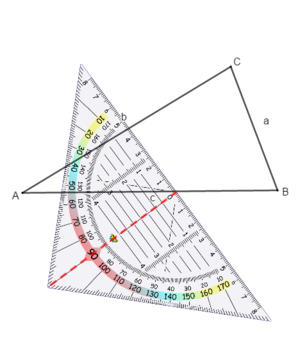
Schiebe den Nullpunkt auf die Seite.

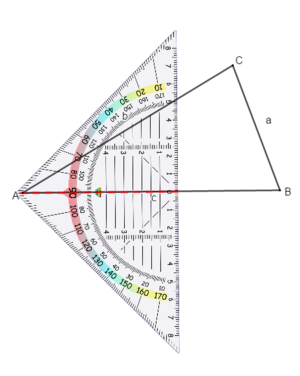
Drehe das Geodreieck so, dass die Mittellinie auf der Seite liegt.

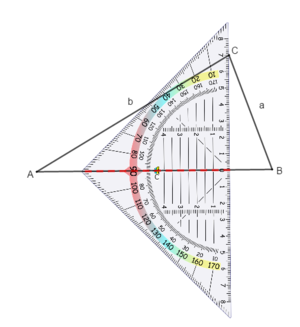
Schiebe das Geodreieck so weit entlang der Seite, bis die Zeichenkante durch den gegenüberliegenden Eckpunkt verläuft.

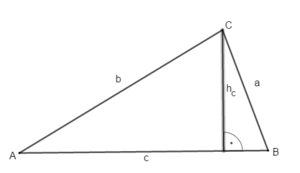
Zeichne und beschrifte die Höhe.

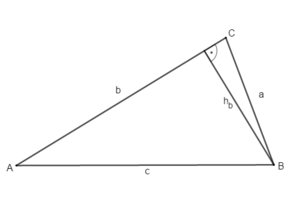
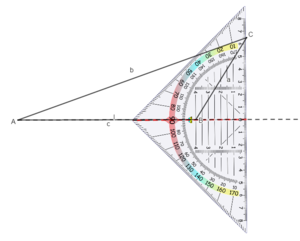
Zeichne ebenso die Höhe h_a zur Seite a:

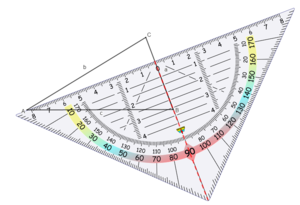
... und die Höhe h_b zur Seite b:

In einem stumpfwinkligen Dreieck verlaufen die Höhen teils außerhalb des Dreiecks. Die Dreiecksseite muss verlängert werden, um die Höhe einzeichnen zu können:

Übe zunächst das Einzeichnen der Höhen mit dem nachfolgenden Applet:

Übung 11: Höhen zeichnen

Zeichne auf dem AB Nr. 2 alle Höhe ein. Eventuell musst du die Seiten verlängern.

Nun versuche, mithilfe des GaeoGebra-Applets die Formel für den Flächeninhalt eines Dreiecks herzuleiten. Notiere deine Ideen.
Bearbeite die nachfolgenden Applets Schritt für Schritt.

Du kannst die Formel für den Flächeninhalt eines Dreiecks auch anders herleiten:

Flächeninhalt und Umfang eines Dreiecks

NOCH ERGÄNZEN
Der Flächeninhalt A eines Dreiecks wird folgendermaßen berechnet:
A = $\tfrac{\text{a*h}}{2}$ = $\tfrac{\text{b*h}}{2}$ = $\tfrac{\text{c*h}}{2}$; allgemein: A = $\tfrac{\text{g*h}}{2}$

Der Umfang u eines Dreiecks wird berechnet mit

u = a + b + c.

Übung 12

Löse Buch

• S. 88 Nr. 1
• S. 88 Nr. 2

Umstellen der Formel

Um die Länge einer Seite oder Höhe zu berechnen, müssen die Formeln für den Flächeninhalt bzw. Umfang umgestellt werden.
1. Stelle die Flächeninhaltsformel um nach der Seitenlänge und nach der Länge der Höhe.
2. Stelle die Umfangsformel nach einer Seitenlänge um.

Umstellen nach einer Seite:

A = a∙h_a   |:h_a
$\tfrac{A}{ha}$ = a
a = $\tfrac{A}{ha}$

Umstellen nach einer Höhe:

A = a∙h_a   |:a
$\tfrac{A}{a}$ = h_a

h_a = $\tfrac{A}{a}$

Übung 13

Löse Buch

• S. 85 Nr. 6

Notiere die Formel und stelle sie nach der gesuchten Größe um. Setze dann ein und berechne.

Übung 14: Anwendungsaufgaben zu Dreiecken

Löse die Anwendungsaufgaben übersichtlich. Notiere zunächst die gegebenen Größen. Zeichne eine Skizze und beschrifte diese. Überlege, was gesucht ist. Unterscheide zwischen Flächeninhalt A(innen drin) und Umfang u (drum herum).

• S. 89 Nr. 9
• S. 89 Nr. 10
• S. 89 Nr. 11

Tipp 1 zu Nr. 9

Notiere, welche Größen gegeben sind und welche gesucht werden. Fertige eine Skizze an und beschrifte sie mit den gegebenen Größen.

Tipp 2 zu Nr. 9

Die Holzverkleidung hat die Form eines Dreiecks mit der Grundseite g=1,5m und der Höhe h=3,7-2,2=1,5(m).
Lösung zur Kontrolle:A_Holz=1,125m²
Das Fenster hat die Form eines Trapezes mit den Seiten c=1,1+1,5+1,5=3,7(m), a=1,5(m) und der Höhe h=2,2(m).
Du kannst die Glasfläche auch als zusammengesetzte Fläche betrachten:
Ein Rechteck in der Mitte und zwei Dreiecke außen.
Lösung zur Kontrolle:A=5,72m²
Um die Kosten zu berechnen, multipliziere jeweils die Fläche mit dem Preis pro m².

Lösung zur Kontrolle:Gesamtkosten ca.397,11€

Tipp 1 zu Nr. 10

Das Dach des Kirchturms besteht aus 4 Dreiecken. Welche Maße musst du für deine Skizze nutzen? Eine Angabe in der Zeichnung ist überflüssig.

Tipp 2 zu Nr. 10

Eine Dreiecksfläche hat die Grundseite g=5,2m und die Höhe h=7,35m. Die andere Zahlenangabe ist für die Lösung dieser Aufgabe überflüssig!

Um die Dachfläche zu bestimmen, berechne den Flächeninhalt einer Dreiecksfläche und mutlipliziere diese mit 4.
Um die Kosten zu berechnen, multipliziere die Dachfläche mit dem Preis pro m²

Tipp 1 zu Nr. 11

Die Schulhoffläche hat die Form eines rechtwinkligen Dreiecks, von dem ein Rechteck abgezogen werden muss. Der Winkel oben links ist ein rechter Winkel. Daher ist eine der Seiten a und b die Grundseite und die andere Seite ist die Höhe des Dreiecks.

Tipp 2 zu Nr. 11

{{{1}}}

Übung 15

Nachdenkaufgaben: Löse Buch

• S. 89 Nr. 12
• S. 90 Nr. 15

Nutze als Hilfe die nachfolgende Applets. Was geschieht mit dem Flächeninhalt und dem Umfang des Dreiecks. Notiere und erkläre.

4.7) Drachenviereck: Umfang und Flächeninhalt (Sprinteraufgabe)

Leite mithilfe des nachfolgenden GeoGebra-Applets die Formel für den Flächeninhalt eines Drachens (Deltoid) her:

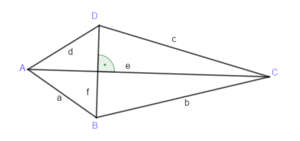
Flächeninhalt und Umfang eines Drachen (Deltiod)

Sind e und f die Diagonalen des Drachen gilt:
A = $\frac{\text{e*f}}{\text{2}}$

Der Umfang u eines Drachen wird berechnet mit

u = a + b + c + d = 2a + 2b (da d=a und c=b) .

Übung 17

Löse Buch

• S. 96 Nr. 5b

Tipp 1 zu Nr. 5b

Um die Tabelle auszufüllen, musst du die Flächeninhaltsformel umstellen:
A = $\frac{\text{e*f}}{\text{2}}$   |∙2
2∙A = e∙f   |:e
$\frac{\text{2*A}}{\text{e}}$ = f   | gegebene Werte einsetzen
$\frac{\text{2*88}}{\text{11}}$ = f   | berechne, denke ans Kürzen

16 (cm) = f

Tipp zu Nr. 5b

Stelle die Formel nach e um:
A = $\frac{\text{e*f}}'''{\text{2}}$   |∙2
2∙A = e∙f   |:f
$\frac{\text{2*A}}{\text{f}}$ = e   | gegebene Werte einsetzen
$\frac{\text{2*76}}{\text{9,5}}$ = e   | berechne, denke ans Kürzen

16 (cm) = e

Tipp 2 zu Nr. 5b

Achte auf gleiche Einheiten! e=380cm = 3,8m
Löse dann wie in Aufgabenteil a)

Tipp 3 zu Nr. 5b

Achte auf gleiche Einheiten! f = 14,5dm = 1,45m
Alternativ kannst du auch die Fläche in dm² angeben:
0,9425m² = 94,25dm² (Verwandlungszahl 100!)Löse dann wie in Aufgabenteil 2)

Bunte Mischung: Üben - Üben - Üben

Übe mit Anton. Logge dich ein und bearbeite die bereitgestellten Übungen.

5) Anwendungsaufgaben