Herta-Lebenstein-Realschule/Lernpfad Gleichungen (mit Klammern)/1) Gleichungen mit Klammern
Aus ZUM Projektwiki
Was ist gegeben?
zwei flächengleiche Flächen (Quadrat und Rechteck)
x = Seitenlänge der quadratischen Weide
x - 4 = eine Seitenlänge der rechteckigen Weide (3m kürzer)
x + 6 = andere Seitenlänge der rechteckigen Weide (5m länger)
Versuche nun eine Gleichung aufzustellen.
Die beiden Weiden sind flächengleich, d.h. ihr Flächeninhalt ist gleich.
Benutze zum Aufstellen der Gleichung die Formeln für die Berechnung des Flächeninhaltes eines Quadrats und eines Rechtecks.
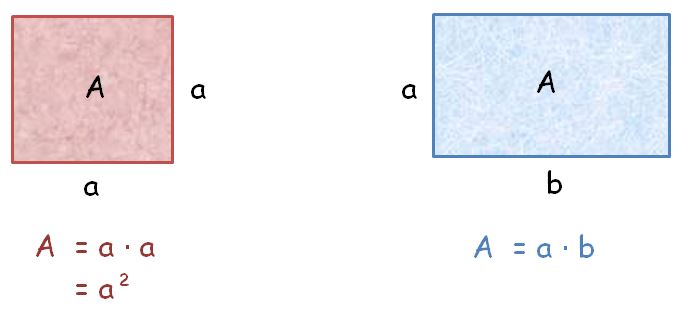
Beide Flächen sind gleich groß, daher lautet die Gleichung:
x² = (x – 4) (x + 6)
Versuche nun x zu berechnen. Löse hierfür zunächst die Klammern auf.
Du hast nun herausgefunden, dass die Länge und Breite der quadratischen Weide je 12m beträgt. Damit kannst du jetzt die Seitenlänge der rechteckigen Weide berechnen. Setze hierfür x = 12 in deine aufgestellten Terme ein:
- x - 4 (eine Seitenlänge des Rechtecks)
- x + 6 (andere Seitenlänge des Rechtecks)




