Informatik am Johanneum/eigene Verfahren/21jojo
Das "Pentadrat" Verfahren
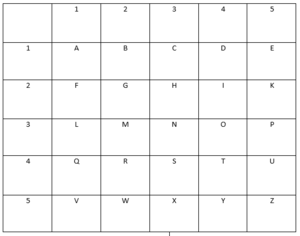
Das Pentradat Verfahren funktioniert wie viele andere Verfahren mit der Hilfe einer quadratischen Tabelle mit 5*5 Zeilen und Spalten. Jeder Zeile und Spalte wird sodann eine Zahl von 1 bis 5 zugeordnet, und die Tabelle wird mit dem Alphabet gefüllt (außer J, denn J wird durch I ersetzt), sodass die Tabelle schließlich so aussehen sollte:
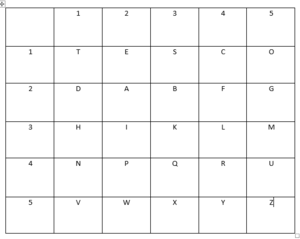
Danach wird ein "Schlüsselwort" gewählt. Dieses Wort muss allerdings nicht wirklich ein echt existierendes Wort, etwas wie jksnea wäre ebenfalls möglich. In meinem Beispiel nutze ich "TESTCODE". Es funktioniert so, das die Buchstaben in die Tabelle eingegeben werden und die restlichen Buchstaben alphabetisch hinten angehängt werden.
Nun können wir jedem Buchstaben zwei Zahlen zuordnen, die der x-Achse und die der y-Achse, wobei die x-Koordinate den Vorrang hat. In unserem Beispiel wäre A also 22 und B 32.
Nun haben wir den Schlüssel, jetzt kommt es zur Verschlüsslung. Unsere Startbotschaft ist "INFORMATIK". Als erstes ordnen wir jedem Buchstaben seine Zahl zu. Also:
23 14 42 51 44 53 22 11 23 33
Doch dies ist nicht genügend. Als nächstes werden die Buchstaben in Paare aufgeteilt (bei ungeraden Buchstabenanzahlen fügt man ein X ans Ende).
23/14 42/51 44/53 22/11 23/33
Nun tauscht man in den jeweiligen Paaren die letzte Ziffer aus.
24/13 41/52 43/54 21/12 23/33
Dies wird schlussendlich wieder gewandelt zu Buchstaben.
P H C G L U E D I K
Durch das Austauschen der Ziffern kann jeder Buchstabe zu mehreren verschiedenen anderen Buchstaben chiffriert werden. So kann man nicht Buchstaben zählen, und so versuchen die Nachricht zu knacken. Zudem kann eine Person ohne den Schlüssel nicht herausfinden welche Zahlenpaare die Buchstabenpaare darstellen und hat so schon Probleme über die erste Hürde zu kommen.