Benutzer:René WWU-6/Testseite

Spielwiese

Schreiben im Wiki

Neben normalem Text kann man auch kursiven oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beidem möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.

Vorlagen

Ganz per Mausklick aktivierbar

Aufgabe

Dies ist eine Aufgabe

Übung

Dies ist eine Übung

Merksatz

Dies ist ein Merksatz

Dateien

Bild aus ZUM Projekte:

Basketball

Bild aus Wikipedia:

Löwe (Panthera leo)

Kombinationen

Aufgabe

Bearbeite folgende Aufgabe

Herme des (um 120 n. Chr.); Kapitolinische Museen, Rom

Integral: Rekonstruieren von Größen

Beispiel

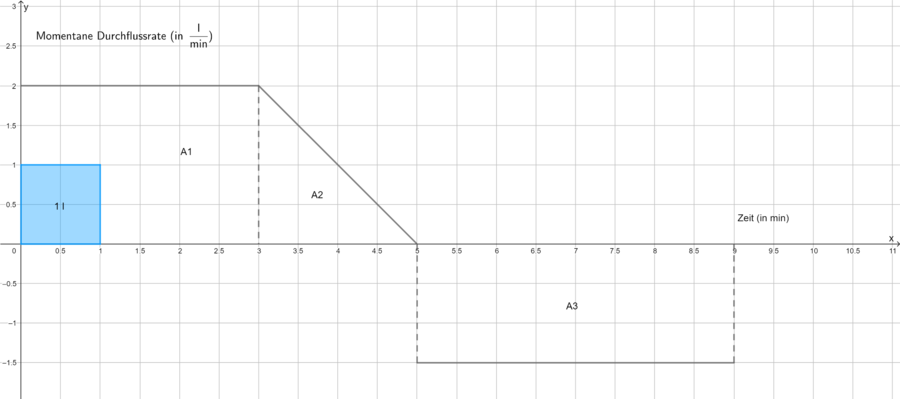
Ein zu Beginn leerer Wassertank wird durch dieselbe Leitung befüllt und entleert. In Figur ist die momentane Durchflussrate f der Leitung für das Intervall [0;9] dargestellt.

Figur 1

Es stellt sich die Frage wie aus der gegebenen Durchflussrate das Gesamtwasservolumen bestimmt werden kann? Dass bedeutet, wie viel Liter Wasser befinden sich nach 9 min im Wassertank?

Es befinden sich nach 9 min 2 Liter im Wassertank.

Im Intervall [0;3] beträgt der Zufluss $2\frac{l}{min}$. In diesen 3 Minuten fließen $2 \frac{l}{min} \cdot 3\ min = 6 l$ in den Tank. 6 ist die Maßzahl des Flächeninhalts A1. Im Intervall [3;5] beträgt die mittlere Zuflussrate $1\frac{l}{min}$. In diesen 2 Minuten kommen $1 \frac{l}{min} \cdot 2\ min = 2 l$ dazu. 2 ist die Maßzahl des Flächeninhalts A2. Im Intevall [5;9] ist die Durchflussrate negativ. Es fließen $1,5 \frac{l}{min} \cdot 4\ min = 6 l$ ab. 6 ist die Maßzahl des Flächeninhalts A3. Man kann also die Gesamtänderung des Wasservolumens in einem Intervall [a;b] mit Flächeninhalten veranschaulichen, wenn man oberhalb der x-Achse liegende Flächen positiv und unterhalb der x-Achse liegenden Flächen negativ zählt. Dieser orientierte Flächeninhalt beträgt beim Wassertank:

A1 + A2 - A3 = 2 Flächeneinheiten

und entspricht einer Volumenänderung von 2 l. Da der Tank zu Beginn leer war, befinden sich jetzt insgesamt 2 l im Tank.

Merke

Ist der Graph einer momentanen Änderungsrate aus gradlinigen Teilstücken zusammengesetzt, so kann man die Gesamtänderung der Größe (Wirkung) rekonstruieren, indem man den orientierten Flächeninhalt zwischen den Graphen der momentanen Änderungsrate und der x-Achse bestimmt. Den orientierten Flächeninhalt nennt man auch das bestimmte Integral.

Aufgabe 1

Du erkennst, dass der orientierte Flächeninhalt nicht mit dem Wert des Flächeninhalt zwischen Graph und x-Achse übereinstimmt. Bearbeite folgende Aufgabe und nutze Zettel und Stift, um deine Rechnungen festzuhalten.

Aufgabe 3

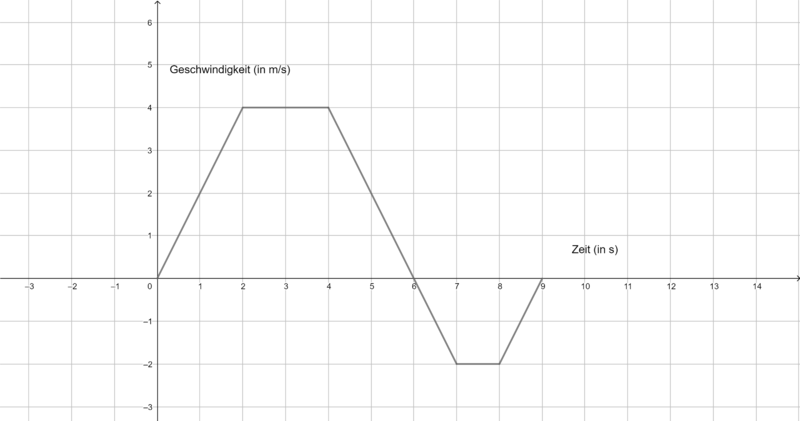
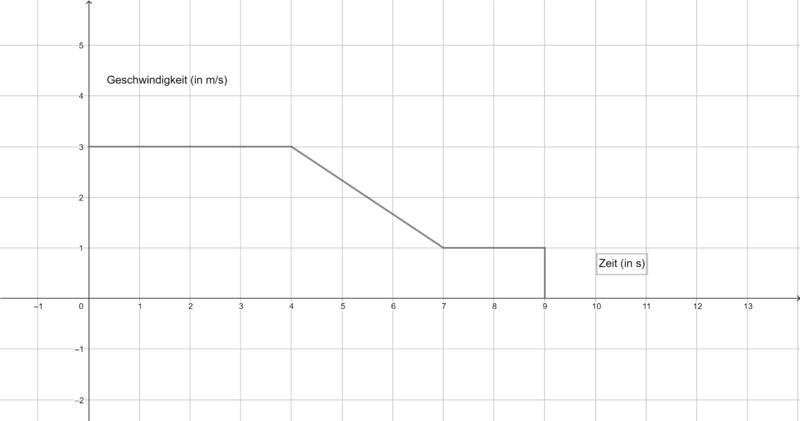
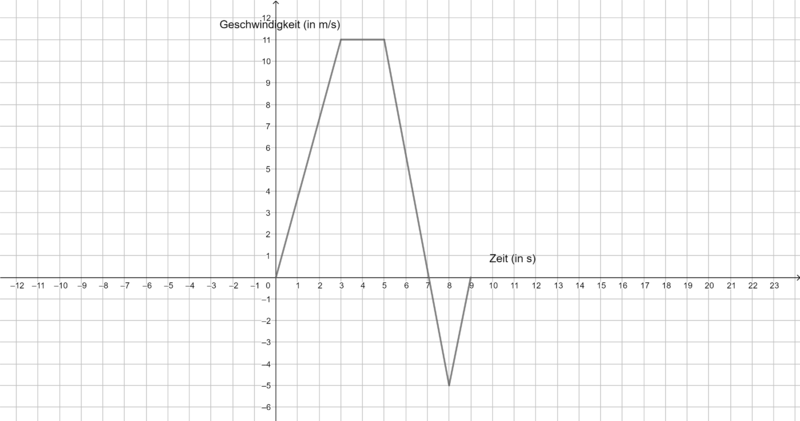
Die folgenden Graphen zeigen die Geschwindigkeit verschiedener Körper. Ermittel jeweils die zurückgelegte Strecke in m nach 9 s. Du benötigst ein Zettel und ein Stift, um deine Rechnungen und Ergebnisse zu notieren.

a)

Figur 1

Lösung

Lösungsweg

b)

Figur 2

Lösung

Lösungsweg

c)

Figur 3

Lösung

Lösungsweg

Beachte

Betrachte folgendes Applet. Lasse dir mithilfe von diesem folgende Funktionen abbilden.

1. f(x)=1
2. f(x)=x
3. f(x)=x^2
4. f(x)=x^3 + x^2 - 1

Was fällt dir auf? Wo besteht der Zusammenhang zwischen der Funktion und seiner Stammfunktion? Wo sind charakteristische Punkte?

Stammfunktion Definition

Eine Funktion F heißt Stammfunktion zu einer Funktion f auf einem Intervall I, wenn für alle x in I gilt:

F'(x) = f(x).

Sind F und G Stammfunktionen von f auf einem Intervall I, dann gibt es eine Konstante c, sodass für alle x in I gilt:

F(x) = G(x)+c

Aufgabe 4

Bearbeite die folgenden Aufgabe. Du benötigst einen Zettel und einen Stift, um deine Rechnungen und Ergebnisse festzuhalten

{{Box|1=Aufgabe 5|2=

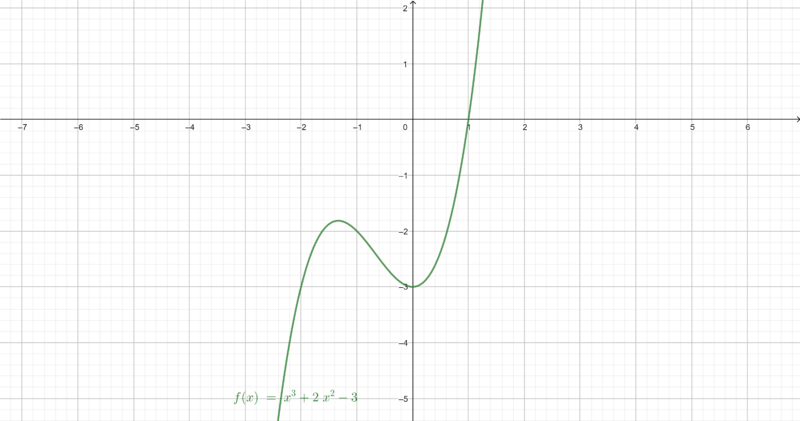
Skizziere eine beliebige Stammfunktion zu folgenden Funktionen auf dem Intervall I=[-5;5]. Zeichne zunächst die Funktion und dann die Stammfunktion auf einen Zettel. Beschreibe dein Vorgehen für charakteristische Punkte (Nullstellen, Extrempunkte, etc.).

a)

f(x)=x^(3)+2x^(2)-3

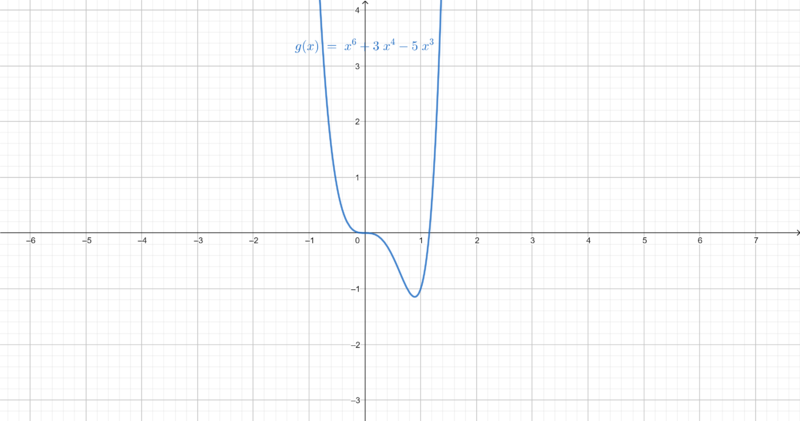
b)

g(x)=x^(6)+3x^(4)-5x^(3)

Satz: Bestimmung von Stammfunktionen

Zur Funktion f mit f(x)=x^r (r≠-1) ist F mit F(x)=(1/r+1)x^(r+1) eine Stammfunktion. Zur Funktion f mit f(x)=x^-1=1/x ist F mit F(x)=ln(x) eine Stammfunktion. Sind G und H Stammfunktionen von g und h, so gilt für die zusammengesetzten Funktionen: f(x)=g(x)+h(x) → F(x)=G(x)+H(X) f(x)=c*g(x) → F(x)=c*G(x)

f(x)=g(c*x+d) → F(x)=1/c *G(c*x+d)

Aufgabe 5

Ordne den Funktionen ihre passende Stammfunktion zu. Ermittel dabei die Stammfunktion auf einem Zettel und ordne anschließend richtig zu.

{{Box|1=Aufgabe 5|2=

Die Funktion f(x)=-x^2+6x gibt die Wachstumsrate von Bakterien an, x in Stunden, f(x) in Hundert Bakterien. Zu Beginn waren 200 Bakterien vorhanden.

• a) Wie lautet die Funktion g(t), die die vorhandene Anzahl von Bakterien zum Zeitpunkt t angibt?
• b) Wie viele Bakterien existieren nach 4 Stunden und nach 6 Stunden?

{{Box|1=Aufgabe 5|2=

Bei einem Sprint über 100m treten zwei Läufer gegeneinander an. Läufer A sprintet mit der Geschwindigkeitsfunktion va(t)=0,25t+10*(1-e^-t). Läufer B sprintet mit der Geschwindigkeitsfunktion vb(t)=12*(1-e^-t)+c*t^2 t ist jeweils die Zeit in Sekunden ab dem Start des Laufes und v(t) die Geschwindigkeit der Läufer in Meter pro Sekunde.

• a) Geben sie die Funktionen an, die die zurückgelegte Strecke zum Zeitpunkt t angibt.
• b) Zeige, dass Läufer A ungefähr 9,8 Sekunden benötigt.
• c) Bestimme den Wert von c so, dass der Läufer nach 9,69 Sekunden ins Ziel kommt.
• d) wie viel Meter sind die beiden Läufer nach 5 s von einander entfernt?