Benutzer:Buss-Haskert/Terme 8E

1. Ausmultiplizieren und Ausklammern (• vor der Klammer )

Wiederholung

Skizziere das Rechteck in dein Heft und berechne den Flächeninhalt des gesamten Rechtecks.

Findest du verschiedene Möglichkeiten? Notiere im Heft.

Vergleiche deine Ideen mit denen im nachfolgenden Video:

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

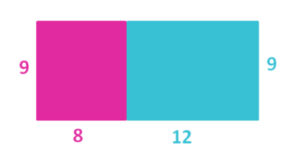
Wie lautet der Name dieses Gesetzes? Notiere dies als Überschrift über die obige Zeichnung in dein Heft.

Das Gesetz heißt Verteilungsgesezt (Distributivgesetz). Wir haben dies umgangssprachlich auch "Jedem die Hand geben" genannt und die Hände als Tipp gezeichnet.

Dieses Gesetz wird im folgenden GeoGebra-Applet noch einmal veranschaulicht. Du kannst die Zahlen durch Variablen ersetzen, indem du die Häkchen "Variable anzeigen" auswählst.
Originallink: https://www.geogebra.org/m/XcFmnc9X

Applet von Birgit Lachner

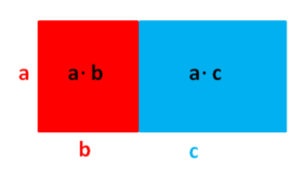
Das Verteilungsgesetz lässt sich auf das Rechnen mit Variablen und Termen übertragen:

Verteilungsgesetz (Distributivgesetz)

Zeichne die Figur in dein Heft und fülle die Lücken im Merksatz. Schreibe ihn in dein Heft ab.

Auch hier ist das große Rechteck aus den kleinen Flächen zusammengesetzt. Der Flächeninhalt kann auf zwei Arten angegeben werden:

als Produkt der Seitenlängen a ⋅ ⟨b+c⟩ und als Summe der einzelnen Flächen a⋅b + a⋅c

Es gilt also: a⋅(b+c) = a⋅b + a⋅c.

Übung 1: Verteilungsgesetz: Rechnen mit Rechtecken

Löse zur Übung die nachfolgenden LearningApps.

1.1 Ausmultiplizieren

Durch Ausmultiplizieren wird ein Produkt in eine Summe umgewandelt, die Klammern werden also aufgelöst.

Hefteintrag: Ausmultiplizieren

Beim Ausmultiplizieren wird jeder Summand in der Klammer mit dem Faktor vor/nach der Klammer multipliziert.

Tipp: "Jedem die Hand geben"

Beispiele:

a)

Produkt Summe

2⋅(x + 5) = 2⋅x + 2⋅5

                = 2x + 10

b)

Produkt Summe

(a + 3b)⋅2c = a⋅2c + 3b⋅2c

                    = 2ac + 6bc

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Übung 5 Überflüssige Malpunkte

Um Produktterme so einfach wie möglich zu schreiben, dürfen überflüssige Malpunkte weggelassen werden. Dies sind Malpunkte zwischen einer Zahl und einer Variablen und zwischen einer Zahl oder Variablen und einer Klammer.Markiere die überflüssigen Malpunkte in den Termen.

Übung 6 Ausmultiplizieren

Löse die Klammern auf und vereinfache den Term so weit wie möglich.

1.2 Ausklammern

Beim Ausklammern wird eine Summe in ein Produkt umgewandelt, es werden also Klammern hinzugefügt. Dies ist nur dann möglich, wenn die Summanden gemeinsame Faktoren haben.

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Ausklammern

Gemeinsame Faktoren in einer Summe können ausgeklammert werden.
Beispiel:
8x + 12xy
= 4x⋅2 + 4x⋅3y

= 4x⋅(2 + 3y)

Übung 8 Ausklammern

Suche in den LearningApps nach gemeinsamen Faktoren der Summenden und klammere diese dann aus.

Zusätzliche Übungen zum Ausklammern (bei Bedarf)

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 50
• 51
• 52

2. Werte von Termen berechnen

Die Term Maschine

Beschreibe, wie die Term Maschine funktioniert

Originallink: https://www.geogebra.org/m/n6cttesM

von Beraterinnen und Beratern für Unterrichtsentwicklung Mathematik

Merke: Werte von Termen berechnen

Wenn du für die Variablen Zahlen einsetzt, lässt sich der Wert des Terms berechnen.

Beispiele:

5∙x für x = 7

5∙7 = 35

4 ∙y - 10 für y = 2

4 ∙2 - 10    |Punkt-vor Strich
= 8 - 10

= -2

Video laden

YouTube

YouTube sammelt möglicherweise persönliche Daten. Datenschutzrichtlinie

FortfahrenAusblenden

Im nachfolgenden Applet kannst du die Werte für a und b mithilfe der Schieberegler verändern. Beschreibe, wie jeweils die Werte der beiden Terme berechnet werden.
Originallink https://www.geogebra.org/m/twss59dq

Haben die Terme 3a + 4b und 7ab immer denselben Wert? Begründe.

Übung 2

Berechne den Wert des Terms 5∙x für
a) x = 8
b) x = -3
c) x = $\tfrac{3}{10}$

d) x = -1,5

Erinnerung: Du multiplizierst einen Bruch mit einer Zahl, indem du den Zähler mit der Zahl multiplizierst und den Nenner beibehältst:

5∙$\tfrac{3}{10}$ = $\tfrac{5}{1}\cdot\tfrac{3}{10} = \tfrac{5\cdot3}{10}$ = ... Denke ans Kürzen!

Übung 3 - Werte von Termen berechnen

Löse auf der Seite Aufgabenfuchs die Aufgaben

• 2
• 9
• 10
• 11

Übung 5

Wähle aus der App-Matrix mindestens 2 Übungen aus und löse diese.

Weitere Übungen (für Schnellrechner)

Bearbeite die nachfolgenden Übungen.

• Übung 1
• Übung 2
• Übung 3

Arbeitsplan vom 09.09.-12.09.

Übungen Buch S. 14 - Wertetabellen Terme zuordnen

Bearbeite die Aufgabe aus dem Buch

• S. 14, A8
• S. 14, A10

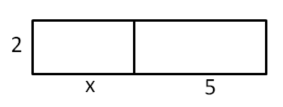
Tipp: Setze für x die Zahlen aus der Wertetabelle ein und schau, welche Zahl du erhältst. Für welche Wertetabelle passt dies?
Beispiel:
Term: A x² + 11; Setze x=1 ein: 1² + 11 = 1+11 = 12 (passt zur Tabelle 3, 4, 8 und 9)
Setze x=2 ein: 2² + 11 = 4+11 = 15 (passt nur zur Tabelle 3)
Also passt die Wertetabelle 3 zum Term A.

S. 14, A10

x	2·(x + 7)	2·x + 14
1	2·(1 + 7) = 2·8 = 16	2·1 + 14 = 2 + 14 = 16
2	2·(2 + 7) = 2·9 = 18	2·2 + 14 = 4 + 14 = 18
3	2·(3 + 7) = 2·10 = 20	2·3 + 14 = 6 + 14 = 20
4	2·(_ + 7) = 2·__ = __	2·_ + 14 = __ + 14 = __

Werte von Terme berechnen - Übungen Buch

Löse im Buch

• S. 13, A5 (Tipp LearningApps unten)
• S. 14, A12

LearningApp zu S. 13, A5
Beispiel: a) x = 4 einsetzen in 2xx+1: 2·4+ 1 = 8 + 1 = 9
b) a = 8 und b = -4 einsetzen in ab: 8·(-4) = -32

Tipp zu S. 14, A12
Überlege, was du rechnen musst, um beim Einsetzen von x die Werte in der rechten Spalte zu erhalten:
1 _____ = 11
2 _____ = 22
Was muss jeweils gerechnet werden?
In diesem Fall muss ·11 gerechnet werden:
11·1 = 11
11·2 = 22
... also lautet der Term 11·x

Übungen im Arbeitsheft

Bearbeite im Arbeitsheft

• S. 3, Nr. 5 (Werte von Termen berechnen)
• S. 3, Nr. 6 (Terme zusammenfassen)

Tipp zu Nr. 5a: Setze für x die gegebenen Werte in den Term ein und berechne:
x=1 in den Term 2x + 5 einsetzen: 2·1 + 5 = 2 + 5 = 7
x=2 in den Term 2x + 5 einsetzen: 2·2 + 5 = 4 + 5 = 9
usw. Tipp zu Nr. 5b: Setze für x die gegebenen Werte in den Term ein und berechne:
x=0 in den Term 3x - 2 einsetzen: 3·0 - 2 = 0 - 2 = -2
x=2 in den Term 3x - 2 einsetzen: 3·2 - 2 = 6 - 2 = 4
usw.
Tipp zu Nr. 5c: Setze für x die gegebenen Werte in den Term ein und berechne:
x=0 in den Term 4x + 1 einsetzen: 4·0 + 1 = 0 + 1 = 1
x=0,5 in den Term 4x + einsetzen: 4·0,5 + 1 = 2 + 1 = 3
usw.
Tipp zu Nr. 5d: Setze für x die gegebenen Werte in den Term ein und berechne:
x=-1 in den Term x : 2 einsetzen: -1 : 2 = -0,5
x=-2 in den Term x : 2 einsetzen: -2 : 2 = -1
usw.
Tipp zu Nr. 5e: Setze für x die gegebenen Werte in den Term ein und berechne:
x=-2,5 in den Term 5 - 2x einsetzen: 5 - 2·(-2,5) = 5 - (-5) = 5 + 5 = 10
x=-2 in den Term 5 - 2x einsetzen: 5 - 2·(-2) = 5 - (-4) = 5 + 4 = 9
...
x=0,5 in den Term 5 - 2x einsetzen: 5 - 2·0,5 = 5 - 1 = 4
usw.