Spielwiese
Mengenangaben anpassen
Der Arzt hat dem Kunden 75 ml von der Creme verschrieben. Das Rezept ist aber für 100 ml ausgelegt. Um genau 75ml herzustellen, musst du die Mengenangaben aus der Rezeptur anpassen.
Aufgabe 4: Mengen umrechnen
 Berechne in Aufgabe 4 auf deinem Arbeitsblatt, wie viel ml du von den jeweiligen Substanzen benötigst.
Berechne in Aufgabe 4 auf deinem Arbeitsblatt, wie viel ml du von den jeweiligen Substanzen benötigst.
Rechne mit dem Dreisatz. Erst berechnest du alle Mengenangaben für 1 ml Creme und anschließend für 75 ml.
Erklärung
Klicke mit der Maus oder mit deinem Finger erst auf die 1 (mittlere Spalte, Reihe 2, Spalte C). Unten rechts von dem Feld erscheint nun ein blaues Viereck. Tippe mit der Maus oder dem Finger darauf bis ein kleines Kreuz an der Stelle kommt und ziehe das Kreuz nach unten bis zum Ende der Tabelle. Es sollten dann in allen Felder dieser Spalte Zahlen stehen. Wiederhole das genauso in der rechten Spalte. In der mittleren Spalte werden dir dann die Mengen in ml für 1 ml Creme angezeigt. In der rechten Spalte werden dir die Mengen in ml für 75 ml Creme angezeigt.
Klicke mit der Maus oder mit deinem Finger erst auf die 1 (mittlere Spalte, Reihe 2, Spalte C). Unten rechts von dem Feld erscheint nun ein blaues Viereck. Tippe mit der Maus oder dem Finger darauf bis ein kleines Kreuz an der Stelle kommt und ziehe das Kreuz nach unten bis zum Ende der Tabelle. Es sollten dann in allen Felder dieser Spalte Zahlen stehen. Wiederhole das genauso in der rechten Spalte. In der mittleren Spalte werden dir dann die Mengen in ml für 1 ml Creme angezeigt. In der rechten Spalte werden dir die Mengen in ml für 75 ml Creme angezeigt.
Schreiben im Wiki
Testseite zur Erstellung einer Unterseite mit zufälligen Funktionen.
Die Wahrscheinlichkeit eine Vier zu würfeln liegt bei  .
.
Als Art der Vorlage kann gewählt werden:
Arbeitsmethode, Merksatz, Hervorhebung1, Info u.v.m.,
Dieser Text ist besser versteckt
Abeitsblatt: Einen eigenen Lernpfad erstellen
"Neben normalen Text kann man auch kursiv oder fett gedruckten Text schreiben. Ebenso ist eine Kombination aus beiden möglich. Grüner Text ist schon etwas schwieriger und funktioniert über die Quelltextbearbeitung.
Einen neuen Absatz beginnt man in der Quelltextverabeitung durch zwei aufeinanderfolgende Zeilenumbrüche, also einer leeren Zeile zwischen den beiden Absätzen. In der visuellen Bearbeitung reicht hierzu das einmalige Betätigen der Eingabetaste."
Vorlagen
Das ist ein Tipp
Info
In diesem Lernpfadkapitel wiederholen wir die Bearbeitung einer Aufgabe mittels Dreisatz.
Für die Bearbeitung dieses Kapitels benötigst du am besten einen Stift und Papier oder dein Tablet zum aufschreiben.
Viel Erfolg!
Beim Dreisatz benutzt du einfache Rechenoperationen um schnell herauszufinden, was z.B. eine bestimmte Anzahl an Objekten kostet. Das Gute ist: Die Vorgehensweise ist dabei immer dieselbe.
Dreisatz (proportional)
Stell dir vor du bestellst für Oma Gretel Hustentabletten für den Monat. Normalerweise kaufst du nur 3 Packungen für 1,50 €, dieses Mal jedoch möchtest du 5 Packungen kaufen, da sie am Ende des Monats in den Urlaub fährt.
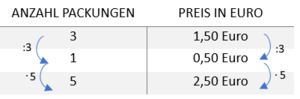
Veranschaulichung eines proportionalen Dreisatzes.
Eine gute Idee ist dazu eine Tabelle zu erstellen, in der du die Rechenschritte aufschreibst.
So gehst du vor:
1. Den Preis von einer Packung berechnen.
Du weißt schon: 3 Packungen kosten 1,50 €.
Dann kostet eine Packung 1,50 € : 3 = 0,50 € = 50 ct.
2. Den Preis von der gesuchten Anzahl an Packungen berechnen.
Das Ergebnis vom 1. Schritt mit der gesuchten Anzahl multiplizieren.
5 Packungen kosten also 0,50 € ⋅ 5 = 2,50 €.
Aufgabe: Dreisatz
Probiere die Anwendung des Dreisatzes nun selbst. Fülle die Tabelle aus. Bestimme die richtige Lösung?
5 Premiumpflaster kosten 1,50 €. Wie viel kosten der Jahresvorrat von 12 Pflastern?
Das ist eine Lösung
Aufgabe 1: Münzwurf
Inhalt
Merksatz: Kongruenzsätze
Inhalt
Beispiel: Polynomdivision
Inhalt
Vom Dreisatz und der Prozentrechnung in der Apotheke
Dieser Lernpfad beschäftigt sich mit dem Dreisatz und Prozentrechnung. Wir schauen zusammen in den Alltag eines*r
Apothekers*in.
- Im ersten Abschnitt wollen wir uns mit den Aufgaben in der Apotheke und den dazugehörigen Konzepten beschäftigen. Dazu sollt ihr euch selbst einschätzen und könnt euch mit der Hilfe dieses Lernpfades erinnern.
- In Aufgabe 1 kannst du die Berechnung mittels Dreisatz anhand von Fallbeispielen aus der Apotheke. Diese Aufgabe ist eine Förderaufgabe.
- In Aufgabe 2 erfährst du mit dem Hilfsmittel MischungsKreuz über die Berechnung der Konzentration.
- In Aufgabe 3 beschäftigst du dich mit der Prozentrechnung. In den Teilaufgaben a) und b) geht es darum, festzustellen, wie sich die beiden Änderungsraten unterscheiden. Dies ist eine Förderaufgabe.
- In Aufgabe 4 sollst du der Buchhaltung helfen und dich mit der einfachen Visualisierung einer GLeichung außeinandersezten. Dies ist eine Zusatzaufgabe
Viel Spaß beim Bearbeiten! :)
Hier geht es weiter: Seite 1
Von den Fähigkeiten im Alltag der Apotheke 1
Um sich entspannt auf die Kunden einlassen zu können muss die Apothekerin Anja in der Lage sein, einen Dreisatz schnell zu überschlagen um Aussagen für die Kunden zu treffen.
Aufgabe 1: Dreisatz
- a) Könntest du einen Dreisatz ohne Probleme bei der folgenden Aufgabe anwenden
Hattest du kein Problem mit dieser Aufgabe bist du wohl schon ein Profi im Umgang mit dem Dreisatz. Fandest du es schwieriger oder möchtest noch einmal exemplarisch eine Aufgabe zum Thema Dreisatz rechnen, schau doch einmal hier:
Dreisatz
Von den Fähigkeiten im Alltag der Apotheke 2
Vielleicht darf Anja die Tablettenpackung nicht anbrechen. Sie sollte eine Aussage darüber machen können, wie viel Prozent der Kur Markus hat, wenn er nur sechs Tabletten kauft.
Aufgabe 2: Anteil in Prozent
- a) Kannst du den Anteil eines Verhältnisses in Prozent leicht berechnen?
Wenn du noch einmal wiederholen möchtest, wie man Anteile in % umrechnet, schaue hier:
Verhältnisse in Prozent
Dateien
Über die Bedienelemente





