Benutzer:ClaraS WWU-7/Testseite

Zufallsversuche

Für die nächsten Aufgaben benötigst du Stift, Papier und Taschenrechner. Bitte runde Dezimalzahlen auf 2 Nachkommastellen.

Zufallsexperimente

Bei Zufallsexperimenten muss zunächst geschaut werden, wie viele mögliche Ereignisse es gibt. Anschließend schaut man, bei wie vielen der Ereignisse ein bestimmter Fall eintritt. Die Wahrscheinlichkeit berechnet sich dann aus $\tfrac{\text{Anzahl der Ereignisse, bei denen der Fall eintritt}}{\text{Anzahl aller Ereignisse}}$.

Baumdiagramme

Zur Darstellung von Wahrscheinlichkeiten hilft es meist, ein Baumdiagramm zu zeichnen. Hierbei wird für jedes Ereignis ein Pfad gezeichnet. Entlang der Pfade stehen die jeweiligen Wahrscheinlichkeiten.

Aufgabe 1: Klassendienste

In einer Klasse sind 14 Jungen und 13 Mädchen. Es werden Beauftragte für verschiedene Klassendienste gelost.

a) Für den Blumendienst wird eine Person gelost. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist?

Zeichne ein Baumdiagramm. Was sind die Ereignisse?

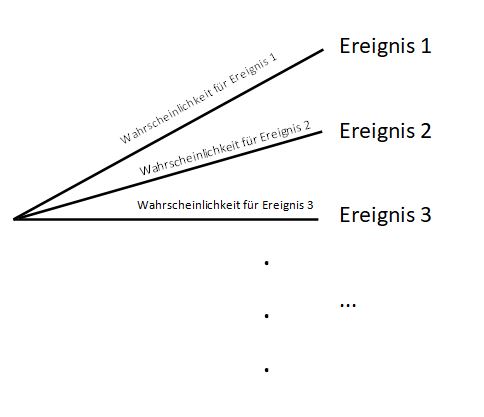
Zeichnet man ein Baumdiagramm, so gibt es zwei Ereignisse:

1. Ein Junge wird gelost.

2. Ein Mädchen wird gelost.

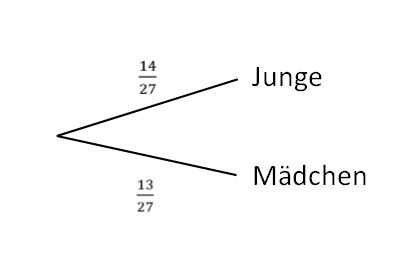
Die Wahrscheinlichekeiten ergeben sich aus den absoluten Häufigkeiten, also der tatsächlichen Anzahl an Jungen und Mädchen geteilt durch die Anzahl der Schülerinnen und Schüler in der Klasse. Das Baumdiagramm sieht dann so aus:

Die Wahrscheinlichkeit, dass ein Junge den Dienst bekommt, liegt also bei $\tfrac{14}{27}$.

b) Auch der Tafeldienst wird gelost, jedoch hat die Lehrperson nun auch einen Zettel mit ihrem Namen hinzugefügt. Wie groß ist die Wahrscheinlichkeit, dass sie den Tafeldienst machen muss?

Wie viele Personen stehen nun zur Auswahl?

Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?

Wenn man ein Baumdiagramm zeichnet, so müssen 3 Ereignisse dargestellt werden:

1. Ein Junge wird gelost.

2. Ein Mädchen wird gelost.

3. Die Lehrperson wird gelost.

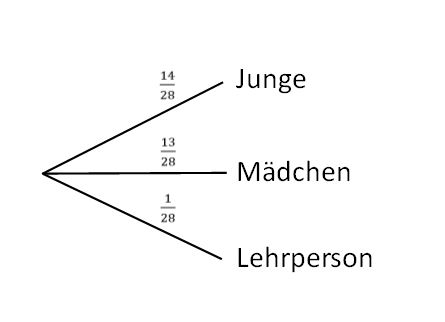
Auch hier ergeben sich die Wahrscheinlichen aus den absoluten Häufigketen. Hierbei muss allerdings darauf geachtet werden, dass nicht nur die Anzahl der Schülerinnen und Schüler als gesamte Menge betrachtet wird, sondern auch die Lehrperson hinzu addiert wird. Es stehen also insgesamt 28 Personen zur Auswahl. Das Baumdiagramm sieht so aus:

Die Wahrscheinlichkeit dafür, dass die Lehrperson selbst die Tafel putzen muss, liegt bei $\tfrac{1}{28}$.

Komplementärregel

Hat ein Experiment genau zwei EReignisse, so spricht man von Ereignis und Gegenereignis. Die Wahrscheinlichkeiten der beiden ergeben in der Summe 1:

$P(E)+P(\bar E)=1$

Aufgabe 2: Schulfest

Bei eurem Schulfest gibt es eine Tombola. Es geht darum, aus einem Glas eine Kugel zuziehen. Bevor du ohne hinzuschauen ziehen darfst, wird dir einmal der Inhalt des Glases gezeigt, du zählst die Kugeln. Außerdem steht ein Schild neben der Urne (Abbildung 2). Du kannst auf die Bilder klicken, um sie in vergrößerter Form zu sehen.

Abbildung 1

Abbildung 2

Es sind 20 blaue Kugeln, 12 rote, 9 gelbe und 3 grüne.

Nun ziehst du ohne hinzuschauen eine Kugel.

a) Wie groß ist die Wahrscheinlichkeit, dass du einen Stift gewinnst (gelbe Kugel)? Gib die Lösung in Prozent an.

Zeichne ein Baumdiagramm. Wie viele Ereignisse gibt es?

Hier kann man das Baumdiagramm auf 2 Arten zeichnen.

Man kann eines mit 4 Ereignissen zeichnen:

1. Die Kugel ist grün.

2. Die Kugel ist gelb.

3. Die Kugel ist rot.

4. Die Kugel ist blau.

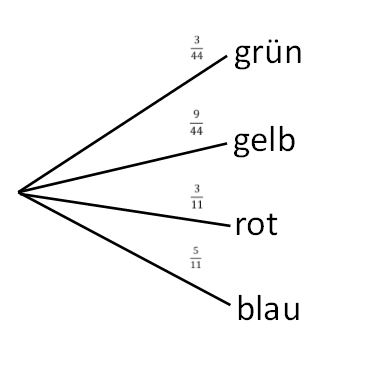
Die Wahrscheinlichkeit errechnet sich dann aus der absoluten Häufigkeit der Kugeln. Das Baumdiagramm sieht dann so aus:

Optional kann man man eines mit 2 Ereignissen zeichnen:

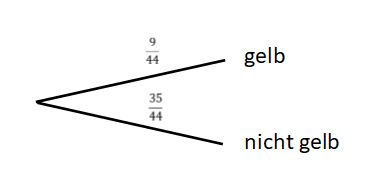
1. Die Kugel ist gelb.

2. Die Kugel ist nicht gelb.

Die Wahrscheinlichkeit dafür, dass die Kugel gelb ist, ergibt sich dann aus der absoluten Häufigkeit der gelben Kugeln. Die Wahrscheinlichkeit dafür, dass die Kugel nicht gelb ist efolgt aus der Komplementärregel.

Das Baumdiagramm sieht dann so aus:

Rechne das nun in Prozent um: Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \tfrac{9}{44} \approx 0,2045 = 20,45 %.}

Die Wahrscheinlichkeit einen Stift zu gewinnen liegt bei 20,45%.

b) Oben auf dem Plakat steht: "Hier ist Gewinnen wahrscheinlicher, als Verlieren!". Stimmt das? Berechne zunächst die einzelnen Wahrscheinlichkeiten. Gibt die Lösung wieder in Prozent an.

Zeichne ein Baumdiagramm. Wie viele Ausgänge gibt es?

Stimmt die Aussage auf dem Plakat?

	ja
	nein

Auch hier kann das Baumdiagramm auf 2 Arten gezeichnet werden:

Man kann eines mit 4 Ereignissen zeichnen:

1. Die Kugel ist grün.

2. Die Kugel ist gelb.

3. Die Kugel ist rot.

4. Die Kugel ist blau.

Die Wahrscheinlichkeit errechnet sich dann aus der absoluten Häufigkeit der Kugeln. Das Baumdiagramm sieht dann so aus:

Optional kann eines mit 2 Ereignissen gezeichnet werden:

Die Wahrscheinlichkeit für das Gewinnen ergibt sich aus der Komplementärregel. Die absolute Häufigkeit der blauen Kugeln, mit denen man verliert, liegt bei $\tfrac{20}{44}=\tfrac{5}{11}$. Die Komplementärregel ergibt dann für das Gewinnen: $1-\tfrac{5}{11}=\tfrac{6}{11}$.

Das Baumdiagramm sieht dann so aus:

Nun rechnet man die Brüche in Prozent um:

Wahrscheinlichkeit zu verlieren: Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle \tfrac{5}{11} \approx 0,4545 = 45,45 %} .

Wahrscheinlichkeit zu gewinnen: Fehler beim Parsen (Konvertierungsfehler. Der Server („cli“) hat berichtet: „[INVALID]“): {\displaystyle 100%-45,45%=54,55%} .

Die Wahrscheinlichkeit, zu gewinnen liegt bei 54,55 %, die zu verlieren bei 45,45%. Die Aussage stimmt also.

Arbeitsmethode